变分自编码器(五):VAE + BN = 更好的VAE
By 苏剑林 | 2020-05-06 | 299169位读者 |本文我们继续之前的变分自编码器系列,分析一下如何防止NLP中的VAE模型出现“KL散度消失(KL Vanishing)”现象。本文受到参考文献是ACL 2020的论文《A Batch Normalized Inference Network Keeps the KL Vanishing Away》的启发,并自行做了进一步的完善。
值得一提的是,本文最后得到的方案还是颇为简洁的——只需往编码输出加入BN(Batch Normalization),然后加个简单的scale——但确实很有效,因此值得正在研究相关问题的读者一试。同时,相关结论也适用于一般的VAE模型(包括CV的),如果按照笔者的看法,它甚至可以作为VAE模型的“标配”。
最后,要提醒读者这算是一篇VAE的进阶论文,所以请读者对VAE有一定了解后再来阅读本文。
VAE简单回顾 #
这里我们简单回顾一下VAE模型,并且讨论一下VAE在NLP中所遇到的困难。关于VAE的更详细介绍,请读者参考笔者的旧作《变分自编码器(一):原来是这么一回事》、《变分自编码器(二):从贝叶斯观点出发》等。
VAE的训练流程 #
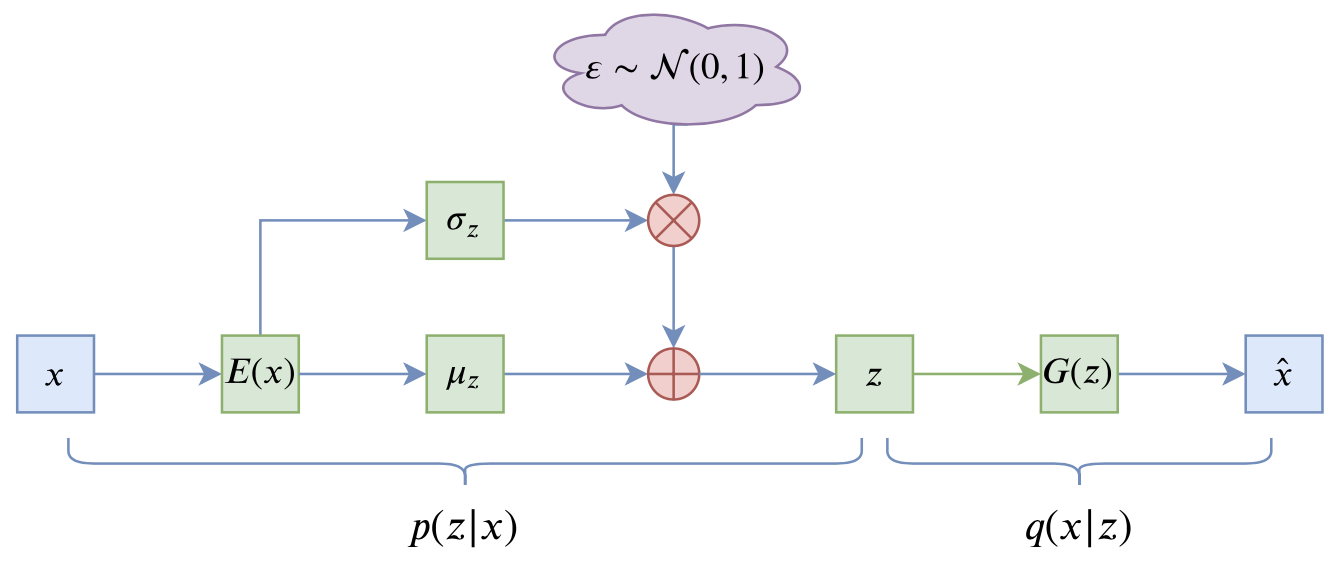
VAE的训练流程大概可以图示为
写成公式就是
$$\begin{equation}\mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)} \Big[\mathbb{E}_{z\sim p(z|x)}\big[-\log q(x|z)\big]+KL\big(p(z|x)\big\Vert q(z)\big)\Big]
\end{equation}$$
其中第一项就是重构项,$\mathbb{E}_{z\sim p(z|x)}$是通过重参数来实现;第二项则称为KL散度项,这是它跟普通自编码器的显式差别,如果没有这一项,那么基本上退化为常规的AE。更详细的符号含义可以参考《变分自编码器(二):从贝叶斯观点出发》。
NLP中的VAE #
在NLP中,句子被编码为离散的整数ID,所以$q(x|z)$是一个离散型分布,可以用万能的“条件语言模型”来实现,因此理论上$q(x|z)$可以精确地拟合生成分布,问题就出在$q(x|z)$太强了,训练时重参数操作会来噪声,噪声一大,$z$的利用就变得困难起来,所以它干脆不要$z$了,退化为无条件语言模型(依然很强),$KL(p(z|x)\Vert q(z))$则随之下降到0,这就出现了KL散度消失现象。
这种情况下的VAE模型并没有什么价值:KL散度为0说明编码器输出的是常数向量,而解码器则是一个普通的语言模型。而我们使用VAE通常来说是看中了它无监督构建编码向量的能力,所以要应用VAE的话还是得解决KL散度消失问题。事实上从2016开始,有不少工作在做这个问题,相应地也提出了很多方案,比如退火策略、更换先验分布等,读者Google一下“KL Vanishing”就可以找到很多文献了,这里不一一溯源。
BN的巧与妙 #
本文的方案则是直接针对KL散度项入手,简单有效而且没什么超参数。其思想很简单:
KL散度消失不就是KL散度项变成0吗?我调整一下编码器输出,让KL散度有一个大于零的下界,这样它不就肯定不会消失了吗?
这个简单的思想的直接结果就是:在$\mu$后面加入BN层,如图
推导过程简述 #
为什么会跟BN联系起来呢?我们来看KL散度项的形式:
\begin{equation}\mathbb{E}_{x\sim\tilde{p}(x)}\left[KL\big(p(z|x)\big\Vert q(z)\big)\right] = \frac{1}{b} \sum_{i=1}^b \sum_{j=1}^d \frac{1}{2}\Big(\mu_{i,j}^2 + \sigma_{i,j}^2 - \log \sigma_{i,j}^2 - 1\Big)\end{equation}
上式是采样了$b$个样本进行计算的结果,而编码向量的维度则是$d$维。由于我们总是有$e^x \geq x + 1$,所以$\sigma_{i,j}^2 - \log \sigma_{i,j}^2 - 1 \geq 0$,因此
\begin{equation}\mathbb{E}_{x\sim\tilde{p}(x)}\left[KL\big(p(z|x)\big\Vert q(z)\big)\right] \geq \frac{1}{b} \sum_{i=1}^b \sum_{j=1}^d \frac{1}{2}\mu_{i,j}^2 = \frac{1}{2}\sum_{j=1}^d \left(\frac{1}{b} \sum_{i=1}^b \mu_{i,j}^2\right)\label{eq:kl}\end{equation}
留意到括号里边的量,其实它就是$\mu$在batch内的二阶矩,如果我们往$\mu$加入BN层,那么大体上可以保证$\mu$的均值为$\beta$,方差为$\gamma^2$($\beta,\gamma$是BN里边的可训练参数),这时候
\begin{equation}\mathbb{E}_{x\sim\tilde{p}(x)}\left[KL\big(p(z|x)\big\Vert q(z)\big)\right] \geq \frac{d}{2}\left(\beta^2 + \gamma^2\right)\label{eq:kl-lb}\end{equation}
所以只要控制好$\beta,\gamma$(主要是固定$\gamma$为某个常数),就可以让KL散度项有个正的下界,因此就不会出现KL散度消失现象了。这样一来,KL散度消失现象跟BN就被巧妙地联系起来了,通过BN来“杜绝”了KL散度消失的可能性。
为什么不是LN? #
善于推导的读者可能会想到,按照上述思路,如果只是为了让KL散度项有个正的下界,其实LN(Layer Normalization)也可以,也就是在式$\eqref{eq:kl}$中按$j$那一维归一化。
那为什么用BN而不是LN呢?
这个问题的答案也是BN的巧妙之处。直观来理解,KL散度消失是因为$z\sim p(z|x)$的噪声比较大,解码器无法很好地辨别出$z$中的非噪声成分,所以干脆弃之不用;而当给$\mu(x)$加上BN后,相当于适当地拉开了不同样本的$z$的距离,使得哪怕$z$带了噪声,区分起来也容易一些,所以这时候解码器乐意用$z$的信息,因此能缓解这个问题;相比之下,LN是在样本内进的行归一化,没有拉开样本间差距的作用,所以LN的效果不会有BN那么好。
进一步的结果 #
事实上,原论文的推导到上面基本上就结束了,剩下的都是实验部分,包括通过实验来确定$\gamma$的值。然而,笔者认为目前为止的结论还有一些美中不足的地方,比如没有提供关于加入BN的更深刻理解,倒更像是一个工程的技巧,又比如只是$\mu(x)$加上了BN,$\sigma(x)$没有加上,未免有些不对称之感。
经过笔者的推导,发现上面的结论可以进一步完善。
联系到先验分布 #
对于VAE来说,它希望训练好后的模型的隐变量分布为先验分布$q(z)=\mathcal{N}(z;0,1)$,而后验分布则是$p(z|x)=\mathcal{N}(z; \mu(x),\sigma^2(x))$,所以VAE希望下式成立:
\begin{equation}q(z) = \int \tilde{p}(x)p(z|x)dx=\int \tilde{p}(x)\mathcal{N}(z; \mu(x),\sigma^2(x))dx\end{equation}
两边乘以$z$,并对$z$积分,得到
\begin{equation}0 = \int \tilde{p}(x)\mu(x)dx=\mathbb{E}_{x\sim \tilde{p}(x)}[\mu(x)]\end{equation}
两边乘以$z^2$,并对$z$积分,得到
\begin{equation}1 = \int \tilde{p}(x)\left[\mu^2(x) + \sigma^2(x)\right]dx = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\mu^2(x)\right] + \mathbb{E}_{x\sim \tilde{p}(x)}\left[\sigma^2(x)\right]\end{equation}
如果往$\mu(x),\sigma(x)$都加入BN,那么我们就有
\begin{equation}\begin{aligned}
&0 = \mathbb{E}_{x\sim \tilde{p}(x)}[\mu(x)] = \beta_{\mu}\\
&1 = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\mu^2(x)\right] + \mathbb{E}_{x\sim \tilde{p}(x)}\left[\sigma^2(x)\right] = \beta_{\mu}^2 + \gamma_{\mu}^2 + \beta_{\sigma}^2 + \gamma_{\sigma}^2
\end{aligned}\end{equation}
所以现在我们知道$\beta_{\mu}$一定是0,而如果我们也固定$\beta_{\sigma}=0$,那么我们就有约束关系:
\begin{equation}1 = \gamma_{\mu}^2 + \gamma_{\sigma}^2\label{eq:gamma2}\end{equation}
参考的实现方案 #
经过这样的推导,我们发现可以往$\mu(x),\sigma(x)$都加入BN,并且可以固定$\beta_{\mu}=\beta_{\sigma}=0$,但此时需要满足约束$\eqref{eq:gamma2}$。要注意的是,这部分讨论还仅仅是对VAE的一般分析,并没有涉及到KL散度消失问题,哪怕这些条件都满足了,也无法保证KL项不趋于0。结合式$\eqref{eq:kl-lb}$我们可以知道,保证KL散度不消失的关键是确保$\gamma_{\mu} > 0$,所以,笔者提出的最终策略是:
\begin{equation}\begin{aligned}
&\beta_{\mu}=\beta_{\sigma}=0\\
&\gamma_{\mu} = \sqrt{\tau + (1-\tau)\cdot\text{sigmoid}(\theta)}\\
&\gamma_{\sigma} = \sqrt{(1-\tau)\cdot\text{sigmoid}(-\theta)}
\end{aligned}\end{equation}
其中$\tau\in(0,1)$是一个常数,笔者在自己的实验中取了$\tau=0.5$,而$\theta$是可训练参数,上式利用了恒等式$\text{sigmoid}(-\theta) = 1-\text{sigmoid}(\theta)$。
关键代码参考(Keras):
class Scaler(Layer):
"""特殊的scale层
"""
def __init__(self, tau=0.5, **kwargs):
super(Scaler, self).__init__(**kwargs)
self.tau = tau
def build(self, input_shape):
super(Scaler, self).build(input_shape)
self.scale = self.add_weight(
name='scale', shape=(input_shape[-1],), initializer='zeros'
)
def call(self, inputs, mode='positive'):
if mode == 'positive':
scale = self.tau + (1 - self.tau) * K.sigmoid(self.scale)
else:
scale = (1 - self.tau) * K.sigmoid(-self.scale)
return inputs * K.sqrt(scale)
def get_config(self):
config = {'tau': self.tau}
base_config = super(Scaler, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
def sampling(inputs):
"""重参数采样
"""
z_mean, z_std = inputs
noise = K.random_normal(shape=K.shape(z_mean))
return z_mean + z_std * noise
e_outputs # 假设e_outputs是编码器的输出向量
scaler = Scaler()
z_mean = Dense(hidden_dims)(e_outputs)
z_mean = BatchNormalization(scale=False, center=False, epsilon=1e-8)(z_mean)
z_mean = scaler(z_mean, mode='positive')
z_std = Dense(hidden_dims)(e_outputs)
z_std = BatchNormalization(scale=False, center=False, epsilon=1e-8)(z_std)
z_std = scaler(z_std, mode='negative')
z = Lambda(sampling, name='Sampling')([z_mean, z_std])
文章内容小结 #
本文简单分析了VAE在NLP中的KL散度消失现象,并介绍了通过BN层来防止KL散度消失、稳定训练流程的方法。这是一种简洁有效的方案,不单单是原论文,笔者私下也做了简单的实验,结果确实也表明了它的有效性,值得各位读者试用。因为其推导具有一般性,所以甚至任意场景(比如CV)中的VAE模型都可以尝试一下。
转载到请包括本文地址:https://kexue.fm/archives/7381
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (May. 06, 2020). 《 变分自编码器(五):VAE + BN = 更好的VAE 》[Blog post]. Retrieved from https://kexue.fm/archives/7381
@online{kexuefm-7381,
title={ 变分自编码器(五):VAE + BN = 更好的VAE},
author={苏剑林},
year={2020},
month={May},
url={\url{https://kexue.fm/archives/7381}},
}











May 9th, 2020
KL Vanishing 就这么被解决了?
基本解决了。发现原来直接设$\gamma=1$是不合理的,刚对文章做了进一步的完善,欢迎再读读
May 12th, 2020
苏神,感觉你的博客中的图都做得很漂亮,你是用什么软件做的图呀?
draw.io
May 18th, 2020
感謝苏老師的 VAE 系列,受益良多
May 18th, 2020
您好,能否麻煩您更詳細解釋 5 到 8 的公式推導呢? 小弟不是很理解
详细解释就是$(6),(7)$。
已理解了,謝謝
May 23rd, 2020
既然假设先验分布为 $\mathcal{N}{(0,1)}$, 那 $\beta_{\sigma}$ 为什么要固定成 $0$ 呢?
我理解的是应该固定成 $1$, 这样就变成原文的式子了
(不知道我哪里理解得不对, 请指正
根据$(8)$式,如果$\beta_{\sigma}=1$,那么$\gamma_{\mu}=\gamma_{\sigma}=0$?那不就是直接KL消失了么...
$\beta_{\sigma}$设置为多少,跟$\mathcal{N}(0,1)$没有什么联系,只不过直觉上来看,就是觉得$\sigma_z(x)$也应该有各向同性,所以设为0。此外如果只根据$(8)$,那么原则上来讲,任何$(-1, 1)$之间的数都可以,但就算这样,从对称性来看也应该选$0$。
May 30th, 2020
苏神您好!
我看了这篇论文,但是在用TensorFlow或Keras写代码实现的时候没太明白那个Beta或gamma参数怎么固定。我理解的是Beta或gamma初始化为一个固定值后,它在模型训练过程中还是会更新,不知道您是如何固定的?
可能是我太菜,希望您不忙的时候能解惑一下,谢谢!
keras的BatchNormalization可以设置scale=False和center=False,这时候只归一化,不添加beta和gamma,你再另外写个自定义层控制beta和gamma即可。不是已经给出了参考实现了么?
May 31st, 2020
苏神好,我不理解的是最后实现的时候,Batch Norm本身里面$\beta$和$\gamma$是可训练参数,后面又连接尺度变换Scaler,来把推导得到的$\gamma_1$和$\gamma_2$带进去,这是把Batch Norm中两个参数当为固定的$\textbf{0}$和$\textbf{1}$来做了吗? 但我没有看到对应固定参数的代码逻辑,这里不太清楚
假设BatchNorm后服从的是 $\mathbb{E}(X) = \beta, \text{Var}(X) = \gamma$ 的分布,此时,再对此进行尺度变换,假设是$s$,此时对应的期望和方差就变成了 $\mathbb{E}(sX) = s\beta, \text{Var}(sX) = s^2*\gamma$ 吗, 按照此种理解,应该不满足上述推导中$\gamma_{\mu}^2 + \gamma_{\sigma}^2=1$的约束了。
不好意思,代码没看仔细,已经解决了,谢谢!
你可以一开始做BN的时候就不加beta和gamma呀,然后你自己通过自定义层来定义特殊形式的beta和gamma
June 8th, 2020
您好,想问一下公式(10)里的两个$\gamma$的公式策略所表示的含义吗?没理解为什么设置成这种形式。
文章已经说得很清楚了啊,完全不看上下文的么...
我们需要$\gamma_{\mu} > 0$,且$\gamma_{\mu}^2+\gamma_{\sigma}^2=1$,$(10)$式所定义得两个$\gamma$满足这个条件。
我明白这里要满足约束条件$\gamma_{\mu}^{2}+\gamma_{\sigma}^{2}=1$。只是不太理解,$\gamma_{\mu}=\sqrt {\tau + (1-\tau)\cdot sigmoid(\theta)}$和$\gamma_{\sigma}=\sqrt {(1-\tau)\cdot sigmoid(-\theta)}$,这两个公式设计的初衷。除了是为了满足约束,还从什么角度导出的这两个形式。
关于平方和为1,基本上很容易想到$\cos^2\theta + \sin^2\theta=1$,理论上从这个恒等式出发构造$\gamma_{\mu},\gamma_{\sigma}$也没问题,但直觉上它有两个问题可能影响优化:1、$\sin\theta,\cos\theta$可能为负,为了保证非负需要加绝对值,不大优雅;2、$\sin\theta,\cos\theta$关于$\theta$都不是单调的,这一点不是很好。
然后我想到可以寻找和等于1的恒等式$a+b=1$,然后也可以构建平方和恒等式$\left(\sqrt{a}\right)^2+\left(\sqrt{b}\right)^2=1$。那么只需要将$\theta$压缩到0~1即可,所以很容易想到用$\text{sigmoid}(\theta)$了,至于$1-\text{sigmoid}(\theta)=\text{sigmoid}(-\theta)$只是一个漂亮的巧合。
June 9th, 2020
谢谢解答,非常感谢。根据你的思路,我把(10)写成了$\gamma_{\mu}=\sqrt {1-\tau \cdot sigmoid(\theta)}$,$\gamma_{\sigma}=\sqrt {\tau \cdot sigmoid(\theta)}$。只不过是跟博客里(10)的图像关于y轴对称的。应该对优化没有别的影响吧。
其实数学上完全等价的($\tau \to 1 - \tau, \theta\to-\theta$),你这样写确实还简单一点,不错~
June 16th, 2020
这种情况下的VAE模型并没有什么价值:KL散度为0说明编码器输出的是0向量,而解码器则是一个普通的语言模型。
该描述中说KL为0时编码器输出为0但编码器不是应当输出后验分布的参数吗?那这样编码器应当输出0向量和1向量呀?还是说我理解错了?
那我改为常数向量吧,哈哈~
谢谢!我还有另外一个疑问,对于公式4我看您在没有对左侧KL做期望的计算下求解出了KL的下界,这边的跳跃我没能跟上希望大神指点。
这倒是,左端忘记补充对样本求期望了,不过右端事实上已经包含了对样本求期望,所以结果是没错的。现在已经补充上去了,感谢反馈。