其中前六题是选择题，具体情况记不起来了，其实也是挺简单的。不过有兴趣的朋友可以在本文的PDF附件查阅到试题（来自“空念远兮”数学网站）。

对了这个PDF文件的参考答案之后，BoJone发现我的选择题全对。而后三道大题我只做了最后两道，解法也和PDF中的不大一样，在此写出来与大家讨论。

1、求证：内角相等的圆内接五边形是正五边形。

这道题是我在最后十五分钟做出来的。一开始想到很多复杂的定理方法，后来发现它可以很简单证明。

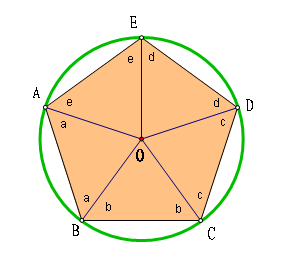
如图是一个满足题目条件的五边形。

五边形

五边形

由于每个三角形都有一个点在圆心，两个点在圆上，所以它们都是等腰三角形。
由内角相等得：
a+b=b+c=c+d=d+e=e+a
而且
$$\begin{aligned}a+b=b+c \Rightarrow a=c;c+d=d+e \Rightarrow c=e \Rightarrow a=c=e \\ b+c=c+d \Rightarrow b=d;d+e=e+a \Rightarrow d=a \Rightarrow b=d=a\end{aligned}$$
所以
a=b=c=d=e。由此得出∠AOB=∠BOC=∠COD=∠DOE=∠EOA。
所以这个五边形是正五边形。证毕。

注：貌似可以推广为“内角相等的圆内接奇数边形是正奇数边形。”

2、求证：$\sqrt{2}+1$的任意正整数次幂都可以表示成$\sqrt{s}+\sqrt{s-1}$的形式，其中s是正整数。

这个问题是我最开始想的（那时刚发下试卷，还没有开始考试）。起初以为可以用数学归纳法，但是发现不怎么能够行得通，就另觅他法可。解法在思想上和PDF中的差不多，只是表达上有所不同。

设$(\sqrt{2}+1)^n=a+b\sqrt{2}=\sqrt{a^2}+\sqrt{2b^2}$，其中a,b都是正整数。
不难证明：
（1）当n是奇数时，有$(\sqrt{2}-1)^n=-a+b\sqrt{2}$；
（2）当n是偶数时，有$(\sqrt{2}-1)^n=a-b\sqrt{2}$。

下面就来证明：
（1）当n是奇数时，$s=a^2+1$，即$2b^2-a^2=1$
（2）当n是偶数时，$s=a^2$，即$a^2-2b^2=1$

第（1）种情况可以解得：
$$\begin{aligned}a=\frac{(\sqrt{2}+1)^n-(\sqrt{2}-1)^n}{2} \\ \sqrt{2} b=\frac{(\sqrt{2}+1)^n+(\sqrt{2}-1)^n}{2}\end{aligned}$$

代入得到$2b^2-a^2=\frac{[(\sqrt{2}+1)^n+(\sqrt{2}-1)^n]^2-[(\sqrt{2}+1)^n-(\sqrt{2}-1)^n]^2}{4}$
$$=\frac{4(\sqrt{2}+1)^n(\sqrt{2}-1)^n}{4}=1$$

第（2）种情况可以解得：
$$\begin{aligned}a=\frac{(\sqrt{2}+1)^n+(\sqrt{2}-1)^n}{2} \\ \sqrt{2} b=\frac{(\sqrt{2}+1)^n-(\sqrt{2}-1)^n}{2}\end{aligned}$$

同理代入得到$a^2-2b^2=1$
证毕

附件：
2012年北约自主招生数学-空念远兮.pdf

2012年北约自主招生数学参考答案-空念远兮.pdf

转载到请包括本文地址：https://kexue.fm/archives/1551

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Feb. 12, 2012). 《2012北约自主招生数学 》[Blog post]. Retrieved from https://kexue.fm/archives/1551

@online{kexuefm-1551,
        title={2012北约自主招生数学},
        author={苏剑林},
        year={2012},
        month={Feb},
        url={\url{https://kexue.fm/archives/1551}},
}