用热传导方程来指导自监督学习

用理论物理来卷机器学习已经不是什么新鲜事了，比如上个月介绍的《生成扩散模型漫谈（十三）：从万有引力到扩散模型》就是经典一例。最近一篇新出的论文《Self-Supervised Learning based on Heat Equation》，顾名思义，用热传导方程来做（图像领域的）自监督学习，引起了笔者的兴趣。这种物理方程如何在机器学习中发挥作用？同样的思路能否迁移到NLP中？让我们一起来读读论文。

基本方程 #

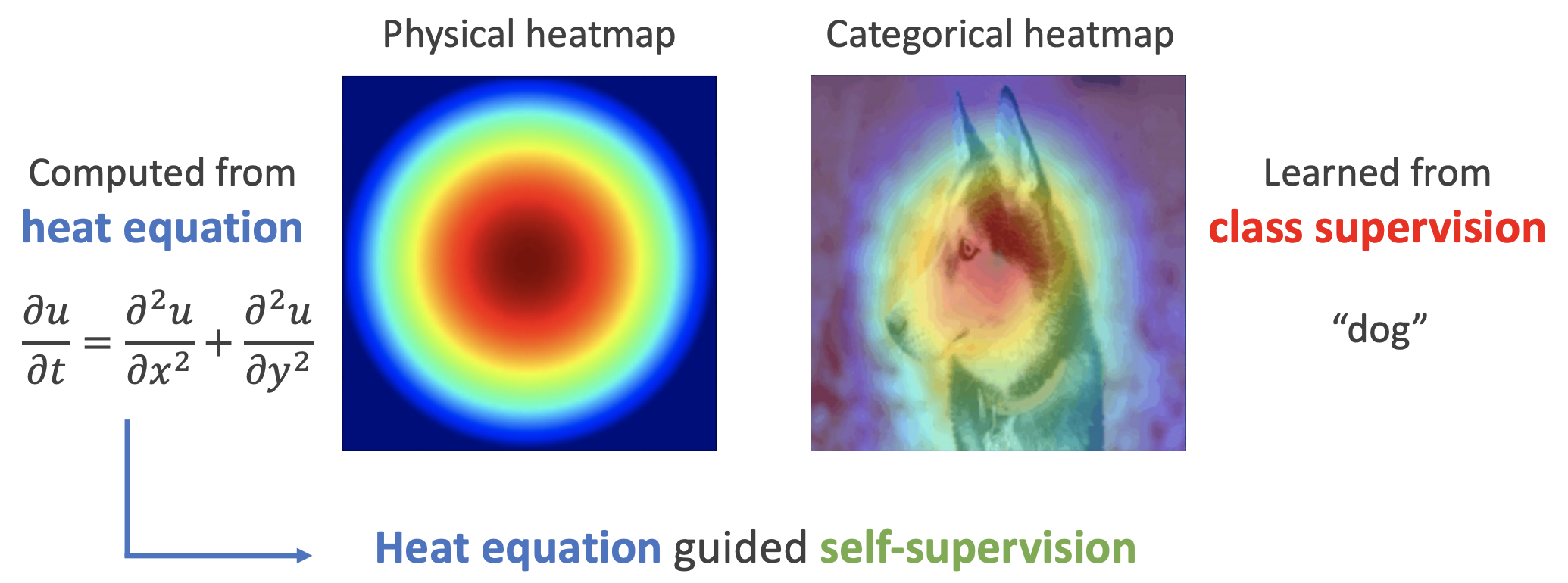
如下图，左边是物理中热传导方程的解，右端则是CAM、积分梯度等显著性方法得到的归因热力图，可以看到两者有一定的相似之处，于是作者认为热传导方程可以作为好的视觉特征的一个重要先验。

具体来说，物理的热传导方程为
\begin{equation}\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\end{equation}
其中$x,y$对应图像的“宽”和“高”两个维度，$u$对应该处的特征值。由于本文主要做的是静态图像而不是视频，所以没有时间维度$t$，为此可以简单地让$\frac{\partial u}{\partial t}=0$。由于特征通常是多维向量而不是标量，所以我们将$u$替换为$\boldsymbol{z}$，得到
\begin{equation}\frac{\partial^2 \boldsymbol{z}}{\partial x^2} + \frac{\partial^2 \boldsymbol{z}}{\partial y^2} = 0\label{eq:laplace}\end{equation}
这被称为“拉普拉斯方程”，它是各向同性的，而图像并不总是各向同性的，所以我们可以补充一个$\boldsymbol{S}$矩阵，来捕捉这种各向异性：
\begin{equation}\frac{\partial^2 \boldsymbol{z}}{\partial x^2} + \boldsymbol{S}\frac{\partial^2 \boldsymbol{z}}{\partial y^2} = 0\label{eq:laplace-s}\end{equation}
然而这是一个二阶方程，后面我们将会看到它在离散化上会比较麻烦，所以作者提出进一步将它转化为一阶方程组
\begin{equation}\frac{\partial \boldsymbol{z}}{\partial x} = \boldsymbol{A}\boldsymbol{z},\quad \frac{\partial \boldsymbol{z}}{\partial y} = \boldsymbol{B}\boldsymbol{z}\label{eq:laplace-1o}\end{equation}
可以验证，只要$\boldsymbol{S} = -\boldsymbol{A}^2(\boldsymbol{B}^2)^{-1}$，那么上式的解必然也是方程$\eqref{eq:laplace-s}$的解，所以原论文以方程$\eqref{eq:laplace-1o}$为出发点。

离散重构 #

说了那么多，其实原论文的思路很简单，它就是认为原始图像经过encoder后得到的特征，应该尽量满足方程$\eqref{eq:laplace-1o}$。具体来说，图像经过encoder后，在global pooling之前，得到的是$w\times h\times d$的feature map，我们将它看成是$m\times n$个$d$维向量，或者说是函数$\boldsymbol{z}(x, y)\in \mathbb{R}^d$，其中$(x,y)$是该向量的位置，那么函数$\boldsymbol{z}(x, y)$应当尽量满足方程$\eqref{eq:laplace-1o}$。

怎么促成这一点呢？根据方程$\eqref{eq:laplace}$，我们可以得到离散化格式
\begin{equation}\begin{aligned}
&\,\boldsymbol{z}(x+\Delta x, y) \approx \boldsymbol{z}(x, y) + \Delta x \boldsymbol{A}\boldsymbol{z}(x,y) = (\boldsymbol{I} + \Delta x \boldsymbol{A})\boldsymbol{z}(x,y) \\
&\,\boldsymbol{z}(x, y+\Delta y) \approx \boldsymbol{z}(x, y) + \Delta y \boldsymbol{B}\boldsymbol{z}(x,y) = (\boldsymbol{I} + \Delta y \boldsymbol{B})\boldsymbol{z}(x,y)
\end{aligned}\label{eq:laplace-delta}\end{equation}
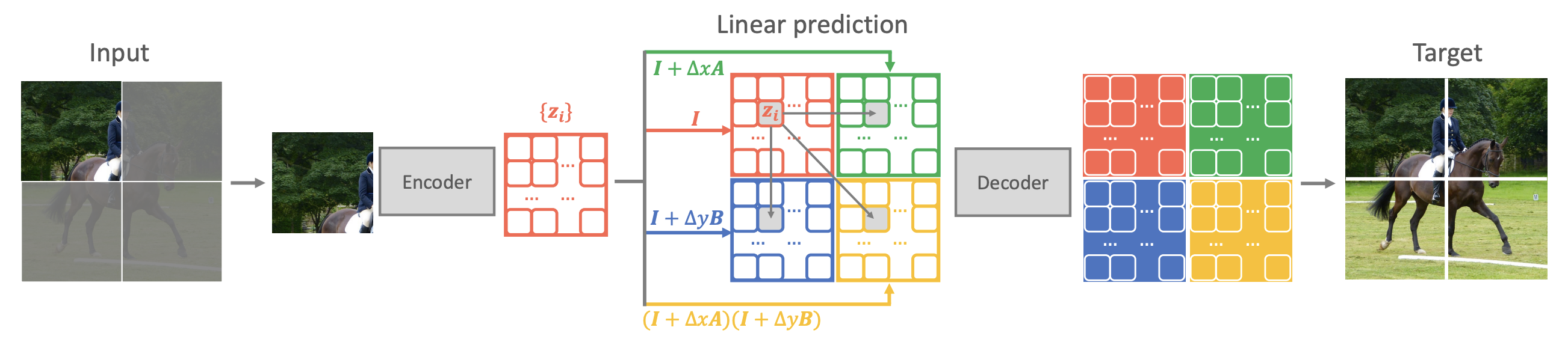
这意味着我们可以通过当前位置的特征来预测邻近位置的特征。于是原论文提出了名为“QB-Heat”的自监督学习方法：

每次只输入一小部分图像，经过encoder后的到对应的特征，通过离散化$ \eqref{eq:laplace-delta}$来预测完整图像的特征，然后将特征传入一个小的decoder来重建完整图像。

示意图如下：

对比分析 #

关于QB-Heat的介绍就到这了，原论文剩下的地方是实验结果以及一些（笔者认为）不大相关的分析，本文就略过了，有兴趣的读者直接看原论文就好。

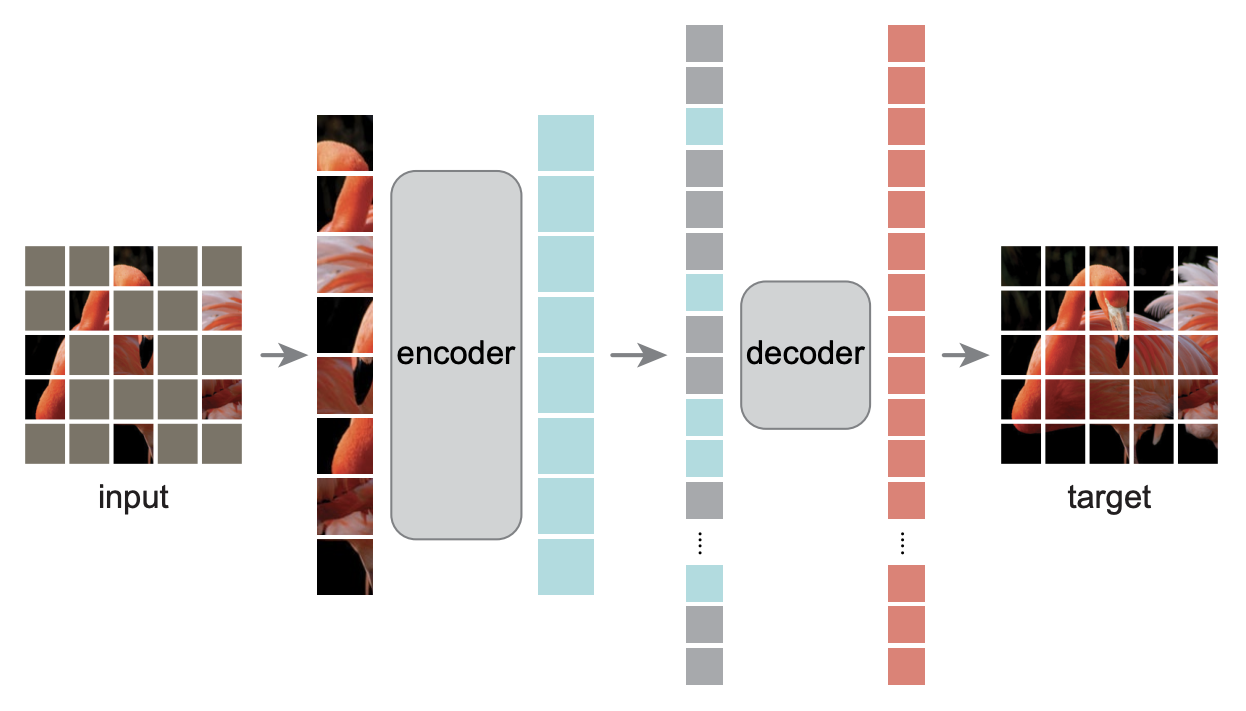
如果读者读过MAE模型（参考《Dropout视角下的MLM和MAE：一些新的启发》），那么应该会感觉QB-Heat跟MAE有很多相似之处——都是输入部分图像到encoder中，然后重构完整图像，同样都是encoder大而decoder小。除了mask方式外，两者最大的不同地方就在于decoder的输入，QB-Heat通过近似$\eqref{eq:laplace-delta}$为图像的剩余部分预测了特征，而MAE则是直接将剩余部分特征当成同一个[MASK]。可以想像，通过近似$\eqref{eq:laplace-delta}$自然会比简单粗暴地填充为[MASK]要更合理些，因此QB-Heat比MAE好也算是情理之中。

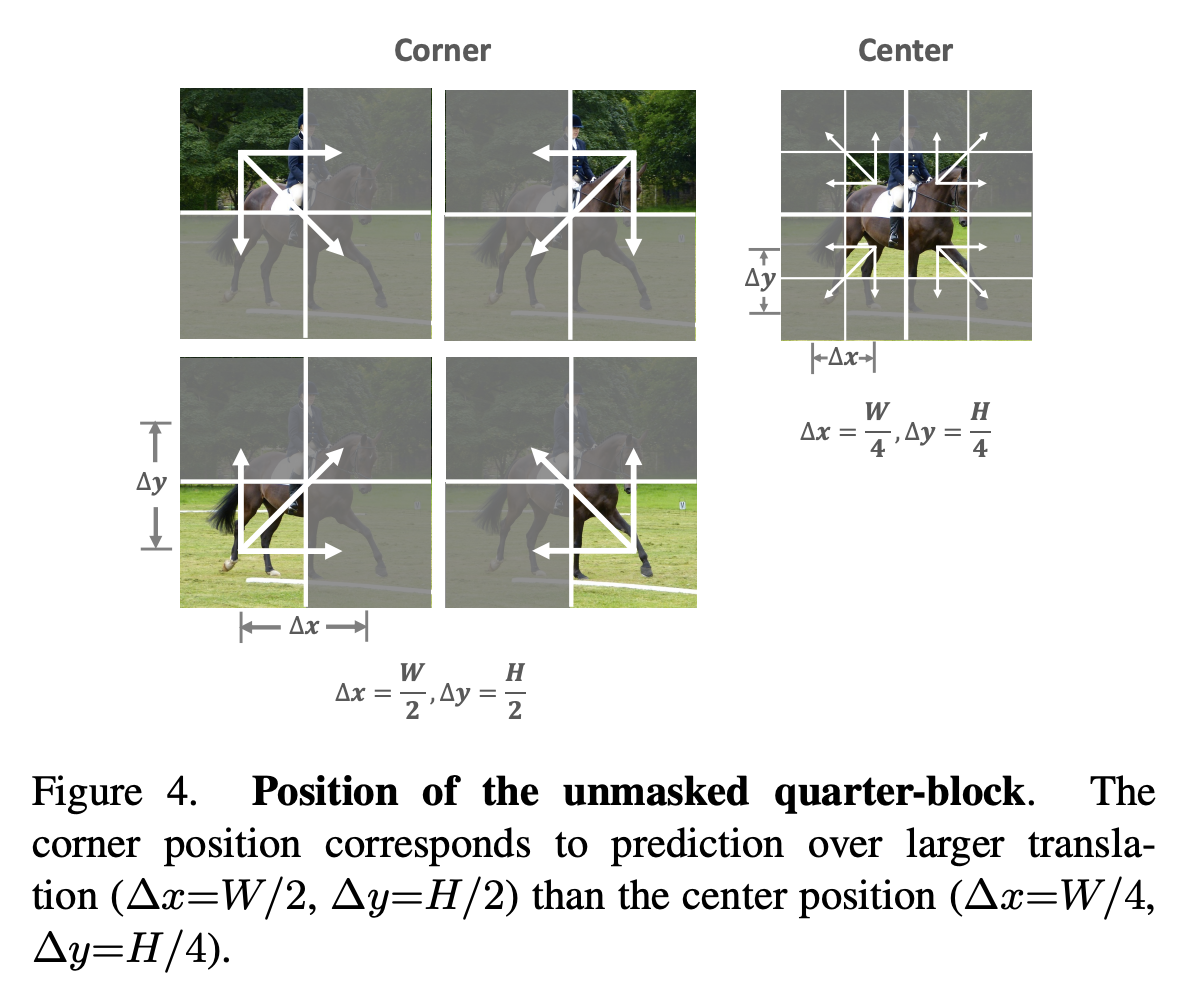
式$\eqref{eq:laplace-delta}$决定了QB-Heat只能通过中心来预测四周（否则中间插值处理起来比较麻烦），因此QB-Heat的mask方式就只能是保留一块连续的方形区域而mask四周，如下图所示。也正是因为QB-Heat的输入是原始图像的一块连续子图，所以它的encoder既可以用Transformer也可以纯CNN模型来搭建。相比之下，MAE是随机mask掉原始图像的一些像素，这样一来要想达到节省encoder计算量的效果，MAE的encoder就只能用Transformer模型，因为只有Transformer模型可以达到缩小序列长度又保留位置信息的效果。

个人思考 #

物理视角看起来固然美妙，但很多时候都只是“幌子”（非贬义），我们更重要的是要透过现象看本质，思考其生效的真正机制。

首先，QB-Heat的一个很明显的“槽点”就是标题和方法都冠以热传导方程之名，但热传导方程的出场时间真的是“不超过3秒”，给人可有可无的感觉。事实上，论文的出发点应该是式$\eqref{eq:laplace}$，即拉普拉斯方程。虽然形式上拉普拉斯方程相当于热传导方程的静态解，但不管是数学上还是物理上的分类和研究，这两者都属于不同的两个分支，所以热传导方程之名实在是有点勉强。其次，拉普拉斯方程也不是用到了原始的式$\eqref{eq:laplace}$或$\eqref{eq:laplace-s}$，而是简化版的式$\eqref{eq:laplace-1o}$，应用时则是对应于近似式$\eqref{eq:laplace-delta}$。撇开物理背景，直接看式$\eqref{eq:laplace-delta}$，它陈述了这样的一个假设：

邻近的特征向量应当尽可能相似，它们之间应当尽可能只差同一个线性变换。

说白了，它通过连续性和线性性假设给特征向量做了显式预测，从而起到了隐式的正则化作用。这不禁让笔者想起了在《从SamplePairing到mixup：神奇的正则项》介绍过的mixup，它也是通过显式构造数据的方式，实则上也给模型加入了隐式的线性正则化，从而增强了模型最终的泛化能力。

对于笔者来说，看到CV中的方法，通常就会想能不能迁移到NLP中去。那么QB-Heat有没有可能做这个迁移呢？相比MAE，QB-Heat做出的最大改动是原始图像的剩余部分特征应当是通过某些假设来预测出来，而不是统一地用[MASK]代替。QB-Heat对CV用的是连续性和线性性假设，那么对于NLP来说能否复制呢？语言本质上是时间序列，只有一个变化维度，这就相当于问能否假设相邻句子之间的句向量相差同一个线性变换？看上去自然语言似乎不应该具有那么好的连续性，但是如果仅仅从线性正则化的角度来理解，又似乎没什么不可行的，毕竟mixup在NLP中的很多任务也work得挺好。

另外，如果是随机mask掉一部分token，而不是像QB-Heat那样只保留连续的一个子区间，那么我们似乎也可以直接用两边位置的特征向量做线性插值来预测中间位置的特征，这样一来也是满足连续性和线性性假设，不知道这样处理效果是否会好？这些都是比较初浅的想法，有待实验验证。

文章小结 #

本文介绍了QB-Heat，这是一种用热传导方程来指导自监督学习的方案，它跟MAE的区别是用简单的预测而不是[MASK]来作为剩余部分图像传入到decoder的特征。

转载到请包括本文地址：https://kexue.fm/archives/9359

更详细的转载事宜请参考：《科学空间FAQ》