科学空间|Scientific Spaces

本文的主题是“为什么我们需要有限的学习率”，所谓“有限”，指的是不大也不小，适中即可，太大容易导致算法发散，这不难理解，但为什么太小也不好呢？一个容易理解的答案是，学习率过小需要迭代的步数过多，这是一种没有必要的浪费，因此从“节能”和“加速”的角度来看，我们不用过小的学习率。但如果不考虑算力和时间，那么过小的学习率是否可取呢？Google最近发布在Arxiv上的论文《Implicit Gradient Regularization》试图回答了这个问题，它指出有限的学习率隐式地给优化过程带来了梯度惩罚项，而这个梯度惩罚项对于提高泛化性能是有帮助的，因此哪怕不考虑算力和时间等因素，也不应该用过小的学习率。

对于梯度惩罚，本博客已有过多次讨论，在文章《对抗训练浅谈：意义、方法和思考（附Keras实现）》和《泛化性乱弹：从随机噪声、梯度惩罚到虚拟对抗训练》中，我们就分析了对抗训练一定程度上等价于对输入的梯度惩罚，而文章《我们真的需要把训练集的损失降低到零吗？》介绍的Flooding技巧则相当于对参数的梯度惩罚。总的来说，不管是对输入还是对参数的梯度惩罚，都对提高泛化能力有一定帮助。

点击阅读全文...

“鸡兔同笼”的那些年

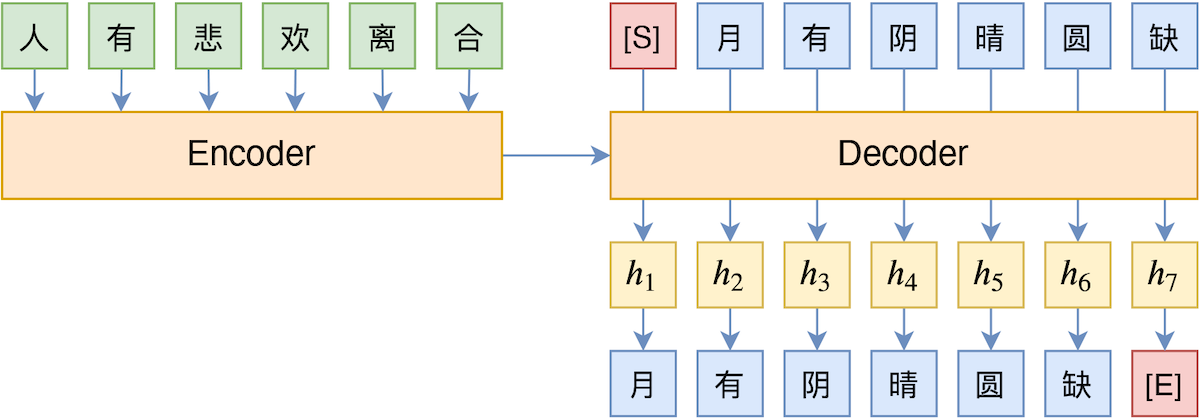
“盈亏问题”、“年龄问题”、“植树问题”、“牛吃草问题”、“利润问题”...，小学阶段你是否曾被各种花样的数学应用题折磨过呢？没关系，现在机器学习模型也可以帮助我们去解答应用题了，来看看它可以上几年级了？

本文将给出一个求解小学数学应用题（Math Word Problem）的baseline，基于ape210k数据集训练，直接用Seq2Seq模型生成可执行的数学表达式，最终Large版本的模型能达到75%的准确率，明显高于ape210k论文所报告的结果。所谓“硬刚”，指的是没有对表达式做特别的转换，也没有通过模板处理，就直接生成跟人类做法相近的可读表达式。

点击阅读全文...

Teacher Forcing是Seq2Seq模型的经典训练方式，而Exposure Bias则是Teacher Forcing的经典缺陷，这对于搞文本生成的同学来说应该是耳熟能详的事实了。笔者之前也曾写过博文《Seq2Seq中Exposure Bias现象的浅析与对策》，初步地分析过Exposure Bias问题。

Teacher Forcing示意图

本文则介绍Google新提出的一种名为“TeaForN”的缓解Exposure Bias现象的方案，来自论文《TeaForN: Teacher-Forcing with N-grams》，它通过嵌套迭代的方式，让模型能提前预估到后$N$个token（而不仅仅是当前要预测的token），其处理思路上颇有可圈可点之处，值得我们学习。

（注：为了尽量跟本博客旧文章保持一致，本文的记号与原论文的记号有所不同，请大家以理解符号含义为主，不要强记符号形式。）

点击阅读全文...

自SimCLR以来，CV中关于无监督特征学习的工作层出不穷，让人眼花缭乱。这些工作大多数都是基于对比学习的，即通过适当的方式构造正负样本进行分类学习的。然而，在众多类似的工作中总有一些特立独行的研究，比如Google的BYOL和最近的SimSiam，它们提出了单靠正样本就可以完成特征学习的方案，让人觉得耳目一新。但是没有负样本的支撑，模型怎么不会退化（坍缩）为一个没有意义的常数模型呢？这便是这两篇论文最值得让人思考和回味的问题了。

其中SimSiam给出了让很多人都点赞的答案，但笔者觉得SimSiam也只是把问题换了种说法，并没有真的解决这个问题。笔者认为，像SimSiam、GAN等模型的成功，很重要的原因是使用了基于梯度的优化器（而非其他更强或者更弱的优化器），所以不结合优化动力学的答案都是不完整的。在这里，笔者尝试结合动力学来分析SimSiam不会退化的原因。

SimSiam

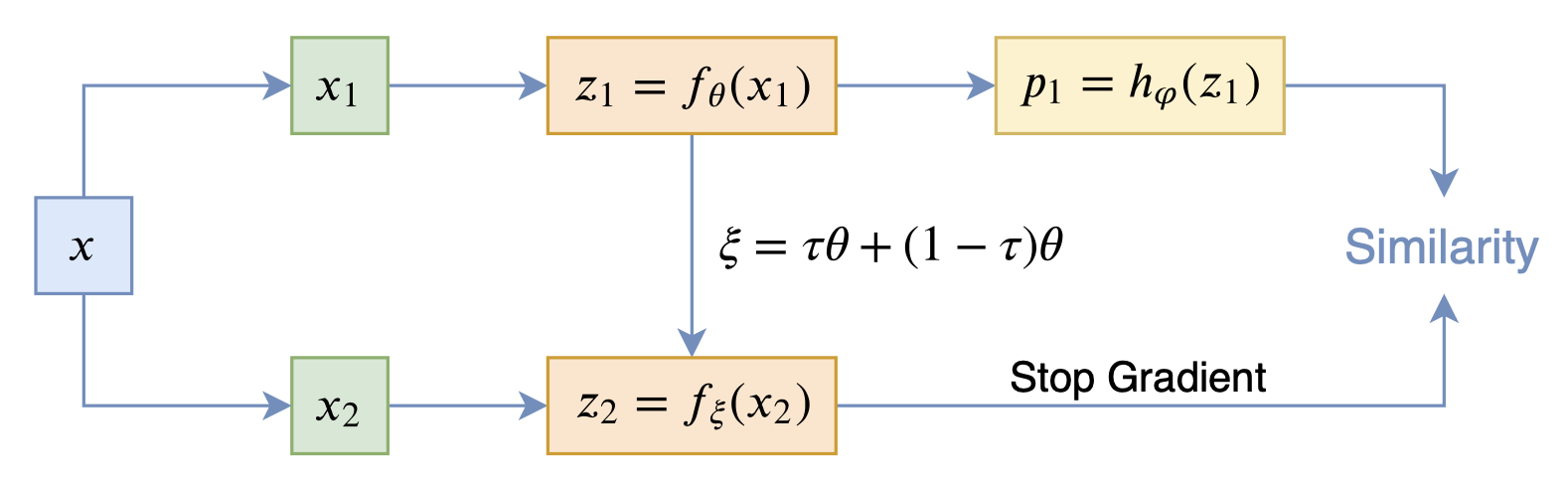
在看SimSiam之前，我们可以先看看BYOL，来自论文《Bootstrap your own latent: A new approach to self-supervised Learning》，其学习过程很简单，就是维护两个编码器Student和Teacher，其中Teacher是Student的滑动平均，Student则又反过来向Teacher学习，有种“左脚踩右脚”就可以飞起来的感觉。示意图如下：

BYOL示意图

点击阅读全文...

中国象棋

不知道读者有没有看过量子位年初的文章《最强写作AI竟然学会象棋和作曲，语言模型跨界操作引热议，在线求战》，里边提到有网友用GPT2模型训练了一个下国际象棋的模型。笔者一直在想，这么有趣的事情怎么可以没有中文版呢？对于国际象棋来说，其中文版自然就是中国象棋了，于是我一直有想着把它的结果在中国象棋上面复现一下。拖了大半年，在最近几天终于把这个事情完成了，在此跟大家分享一下。

象棋谱式
将军不离九宫内，士止相随不出官。
象飞四方营四角，马行一步一尖冲。
炮须隔子打一子，车行直路任西东。
唯卒只能行一步，过河横进退无踪。

点击阅读全文...

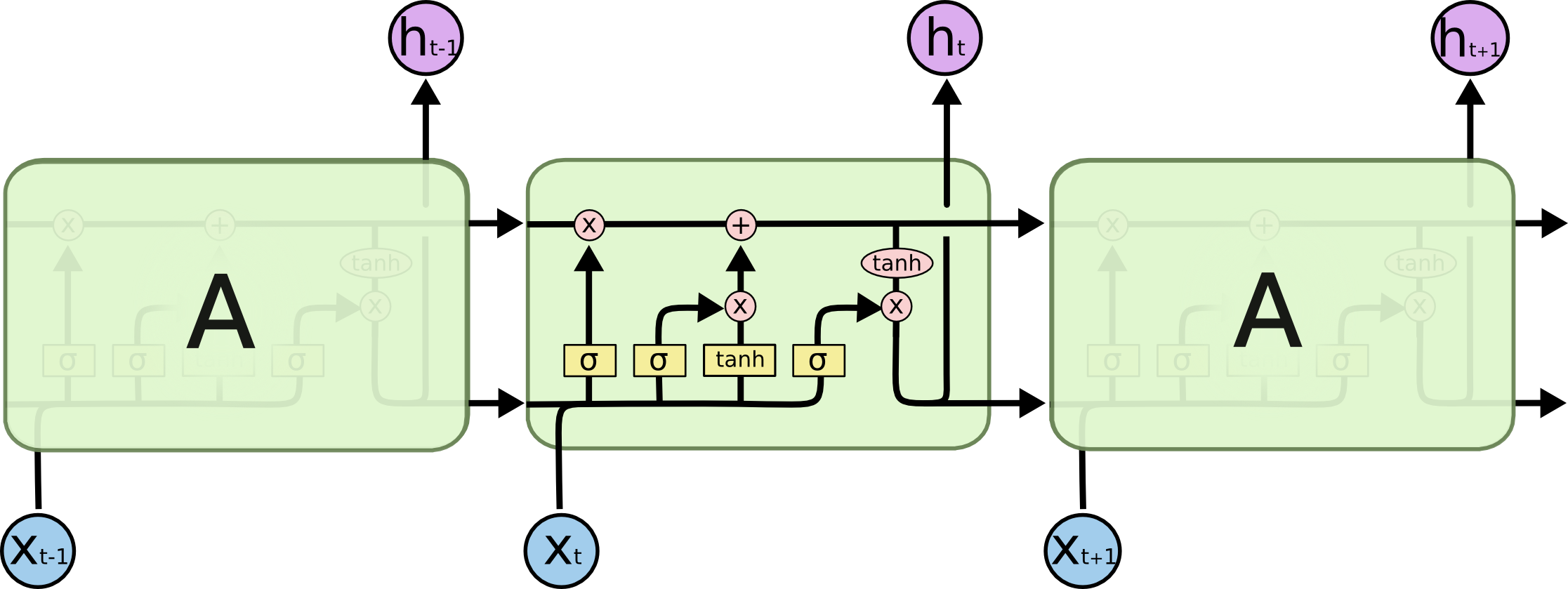
尽管Transformer类的模型已经攻占了NLP的多数领域，但诸如LSTM、GRU之类的RNN模型依然在某些场景下有它的独特价值，所以RNN依然是值得我们好好学习的模型。而对于RNN梯度的相关分析，则是一个从优化角度思考分析模型的优秀例子，值得大家仔细琢磨理解。君不见，诸如“LSTM为什么能解决梯度消失/爆炸”等问题依然是目前流行的面试题之一...

经典的LSTM

关于此类问题，已有不少网友做出过回答，然而笔者查找了一些文章（包括知乎上的部分回答、专栏以及经典的英文博客），发现没有找到比较好的答案：有些推导记号本身就混乱不堪，有些论述过程没有突出重点，整体而言感觉不够清晰自洽。为此，笔者也尝试给出自己的理解，供大家参考。

点击阅读全文...

刚看到一个有意思的结论：

对于任意实数$x$及偶数$n$，总有$\sum\limits_{k=0}^n \frac{x^k}{k!} > 0$，即$e^x$在$x=0$处的偶次泰勒展开式总是正的。

下面我们来看一下这个结论的证明，以及它在寻找softmax替代品中的应用。

证明过程

看上去这是一个很强的结果，证明会不会很复杂？其实证明非常简单，记
\begin{equation}f_n(x) = \sum\limits_{k=0}^n \frac{x^k}{k!}\end{equation}
当$n$是偶数时，我们有$\lim\limits_{x\to\pm\infty} f_n(x)=+\infty$，即整体是开口向上的，所以我们只需要证明它的最小值大于0就行了，又因为它是一个光滑连续的多项式函数，所以最小值点必然是某个极小值点。那么换个角度想，我们只需要证明它所有的极值点（不管是极大还是极小）所对应的函数值都大于0。

点击阅读全文...

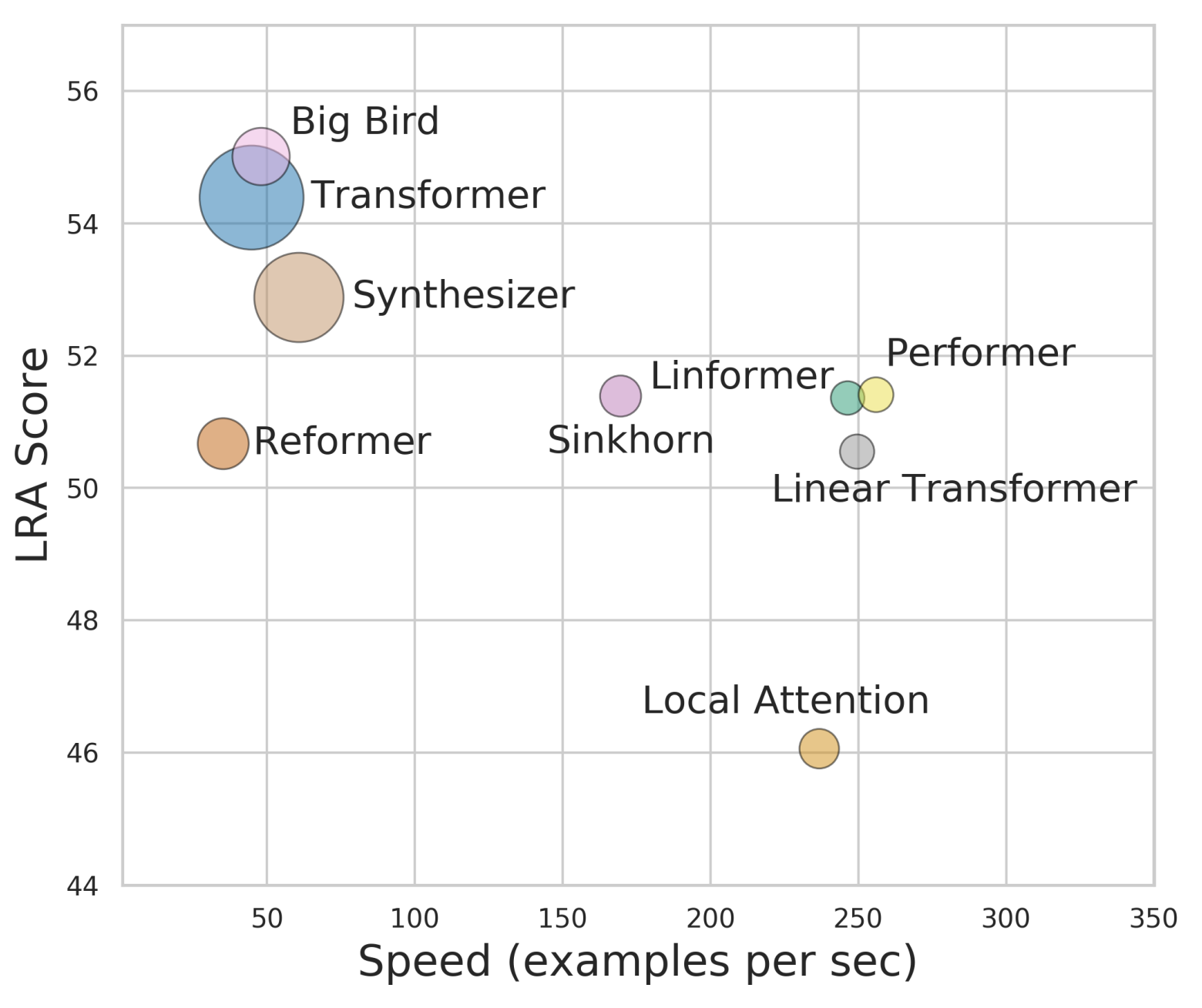
Attention机制的$\mathcal{O}(n^2)$复杂度是一个老大难问题了，改变这一复杂度的思路主要有两种：一是走稀疏化的思路，比如我们以往介绍过的Sparse Attention以及Google前几个月搞出来的Big Bird，等等；二是走线性化的思路，这部分工作我们之前总结在《线性Attention的探索：Attention必须有个Softmax吗？》中，读者可以翻看一下。本文则介绍一项新的改进工作Performer，出自Google的文章《Rethinking Attention with Performers》，它的目标相当霸气：通过随机投影，在不损失精度的情况下，将Attention的复杂度线性化。

各个Transformer模型的“效果-速度-显存”图，纵轴是效果，横轴是速度，圆圈的大小代表所需要的显存。理论上来说，越靠近右上方的模型越好，圆圈越小的模型越好

说直接点，就是理想情况下我们可以不用重新训练模型，输出结果也不会有明显变化，但是复杂度降到了$\mathcal{O}(n)$！看起来真的是“天上掉馅饼”般的改进了，真的有这么美好吗？

点击阅读全文...