TeaForN：让Teacher Forcing更有“远见”一些

Teacher Forcing是Seq2Seq模型的经典训练方式，而Exposure Bias则是Teacher Forcing的经典缺陷，这对于搞文本生成的同学来说应该是耳熟能详的事实了。笔者之前也曾写过博文《Seq2Seq中Exposure Bias现象的浅析与对策》，初步地分析过Exposure Bias问题。

本文则介绍Google新提出的一种名为“TeaForN”的缓解Exposure Bias现象的方案，来自论文《TeaForN: Teacher-Forcing with N-grams》，它通过嵌套迭代的方式，让模型能提前预估到后$N$个token（而不仅仅是当前要预测的token），其处理思路上颇有可圈可点之处，值得我们学习。

（注：为了尽量跟本博客旧文章保持一致，本文的记号与原论文的记号有所不同，请大家以理解符号含义为主，不要强记符号形式。）

Teacher Forcing #

文章《Seq2Seq中Exposure Bias现象的浅析与对策》已经相对详细地介绍了Teacher Forcing，这里仅做简要回顾。首先，Seq2Seq模型将联合概率分解为多个条件概率的乘积，这就是所谓的“自回归模型”：
\begin{equation}\begin{aligned}p(\boldsymbol{y}|\boldsymbol{x})=&\,p(y_1,y_2,\dots,y_n|\boldsymbol{x})\\
=&\,p(y_1|\boldsymbol{x})p(y_2|\boldsymbol{x},y_1)\dots p(y_n|\boldsymbol{x},y_1,\dots,y_{n-1})
\end{aligned}\end{equation}
然后，当我们训练第$t$步的模型$\dots p(y_t|\boldsymbol{x},y_1,\dots,y_{t-1})$时，我们假设$\boldsymbol{x},y_1,\dots,y_{t-1}$都是已知的，然后让模型只预测$y_t$，这就是Teacher Forcing。但在预测阶段，真实的$y_1,\dots,y_{t-1}$都是未知的，此时它们是递归地预测出来的，可能会存在传递误差等情况。因此Teacher Forcing的问题就是训练和预测存在不一致性，这让我们很难从训练过程掌握预测的效果。

没什么远见 #

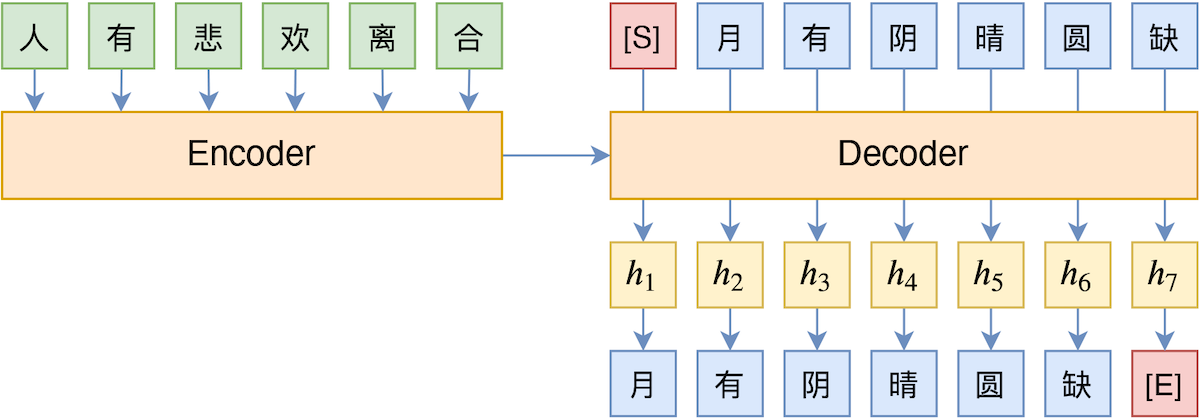
怎么更具体理解这个不一致性所带来的问题呢？我们可以将它理解“没什么远见”。在解码器中，输入$\boldsymbol{x}$和前$t-1$个输出token共同编码得到向量$h_t$，在Teacher Forcing中，这个$h_t$只是用来预测$y_t$，跟$\boldsymbol{y}_{> t}$没有直接联系，换句话说，它的“见识”也就局限在$t$这一步了。

比如上图中的$h_3$向量，Teacher Forcing只让它用来预测“阴”，事实上“阴”的预测结果也会影响“晴”、“圆”、“缺”的预测，也就是说$h_3$也应该与“晴”、“圆”、“缺”有所关联，而Teacher Forcing没有显式地建立这种关联。所以模型在解码的时候每一步很可能只输出局部最高概率的token，这就容易出现高频安全回复或者重复解码现象。

Student Forcing #

为了提高模型的“前瞻能力”，最彻底的方法当然是训练阶段也按照解码的方式来进行，即$h_1,h_2,\dots,h_t$也像解码阶段一样递归地预测出来，不依赖于真实标签，我们不妨称这种方式为Student Forcing。但是，Student Forcing的训练方式来带来两个严重的问题：

第一，牺牲并行。对于Teacher Forcing来说，如果Decoder使用的是CNN或Transformer这样的结构，那么训练阶段是所有token都可以并行训练的（预测阶段还是串行），但如果Student Forcing的话则一直都是串行。

第二，极难收敛。Student Forcing通常需要用Gumbel Softmax或强化学习来回传梯度，它们的训练都面临着严重的不稳定性，一般都要用Teacher Forcing预训练后才能用Student Forcing，但即便如此也不算特别稳定。

形象地理解，Student Forcing相当于老师完全让学生独立探究一个复杂的问题，不做手把手教学，只对学生的结果好坏做个最终评价。这样一旦学生能探索成功，那可能说明学生的能力很强了，但问题就是缺乏老师的“循循善诱”，学生“碰壁”的几率更加大。

往前多看几步 #

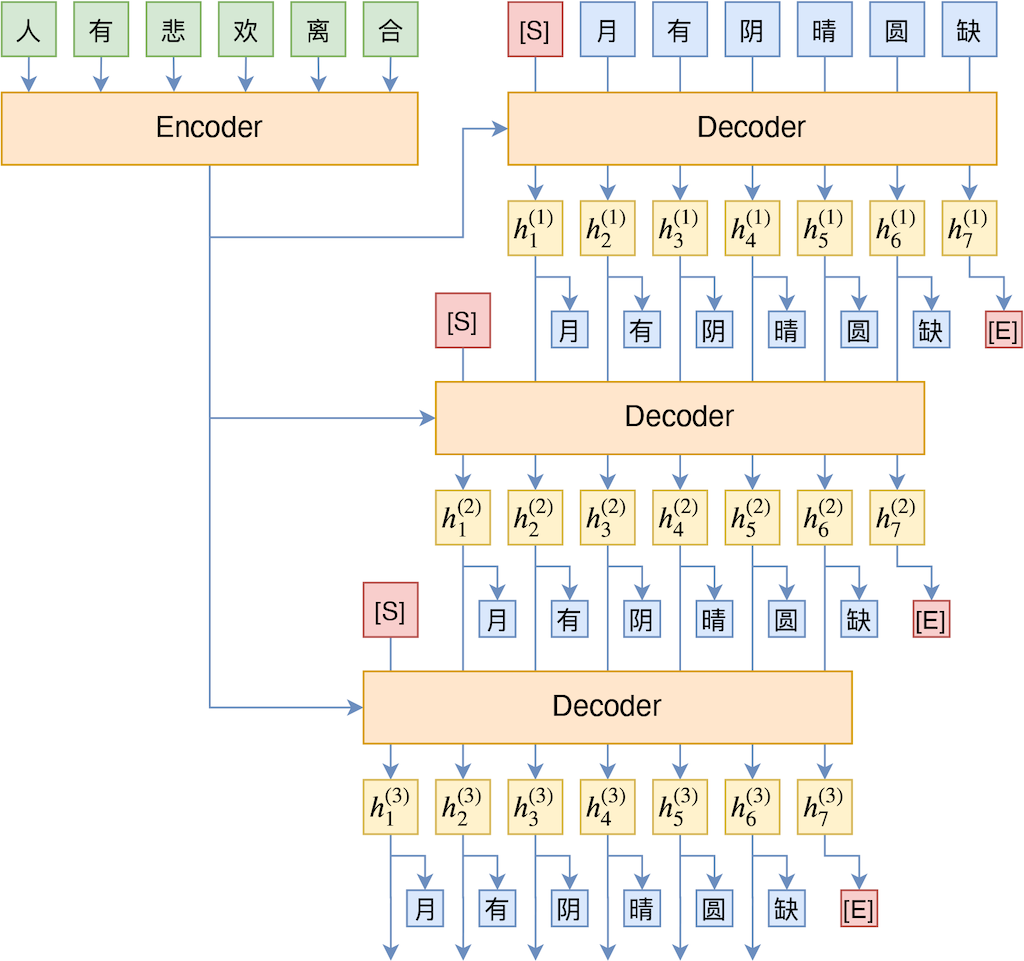
有没有介乎Teacher Forcing与Student Forcing之间的方法呢？有，本文所介绍的TeaForN就算是其中一种，它的思想是常规的Teacher Forcing相当于在训练的时候只往前看1步，而Student Forcing相当于在训练的时候往前看了$L$步（$L$是目标句子长度），如果我们只是往前多看几步（相当于看到了N-gram），那么理论上就能提高“远见”，并且不至于严重牺牲模型的并行性。其示意图如下：

直观来看，就是把输出结果再往前迭代多遍，这样一来前$t-1$个token要预测的就不仅仅是第$t$个token了，还有第$t+1,t+2,\cdots$个。比如在上图中，最后我们用$h_6^{(3)}$来预测了“缺”字，而我们可以看到$h_6^{(3)}$只依赖于“月”、“有”、“阴”三个字，所以我们也可以理解为$h_4^{(1)}$这个向量同时要预测“晴”、“圆”、“缺”三个字，因此也就提高了“远见”。

用数学的话来说 #

用数学语言来描述，我们可以将Decoder分为Embedding层$E$和剩余部分$M$两个部分，Embedding层负责将输入句子$s=[w_0, w_1, w_2, \cdots, w_{L-1}]$映射为向量序列$[e_0, e_1, e_2, \cdots, e_{L-1}]$（其中$w_0$是固定的解码起始标记，也就是上图的[S]，有些文章记为<bos>），然后交给模型$M$处理，得到向量序列$[h_1, h_2, h_3, \cdots, h_L]$，即
\begin{equation}[h_1, h_2, h_3, \cdots, h_L] = M(E([w_0, w_1, w_2, \cdots, w_{L-1}]))\end{equation}
接着通过$p_t = softmax(Wh_t + b)$得到第$t$步的token概率分布，最后用$-\log p_t[w_t]$作为损失函数训练，这便是常规的Teacher Forcing。

可以想象，负责映射到token分布的输出向量序列$[h_1, h_2, h_3, \cdots, h_{L-1}]$某种程度上跟Embedding序列$[e_1, e_2, e_3, \cdots, e_{L-1}]$是相似的，如果我们补充一个$e_0$进去，然后将$[e_0, h_1, h_2, \cdots, h_{L-1}]$也送入到模型$M$中再处理一次，是否可以呢？也就是
\begin{equation}\begin{aligned}[]
\left[e_0,e_1,e_2,\cdots,e_{L-1}\right]& = E\left(\left[w_0, w_1,w_2,\cdots,w_{L-1}\right]\right)\\
\left[h_1^{(1)},h_2^{(1)},h_3^{(1)},\cdots,h_L^{(1)}\right]& = M\left(\left[e_0,e_1,e_2,\cdots,e_{L-1}\right]\right)\\
\left[h_1^{(2)},h_2^{(2)},h_3^{(2)},\cdots,h_L^{(2)}\right]& = M\left(\left[e_0, h_1^{(1)},h_2^{(1)},\cdots,h_{L-1}^{(1)}\right]\right)\\
\left[h_1^{(3)},h_2^{(3)},h_3^{(3)},\cdots,h_L^{(3)}\right]& = M\left(\left[e_0, h_1^{(2)},h_2^{(2)},\cdots,h_{L-1}^{(2)}\right]\right)\\
&\,\,\vdots
\end{aligned}\end{equation}
然后每一个$h$我们都算概率分布$p_t^{(i)} = softmax(Wh_t^{(i)} + b)$，最后算交叉熵并加权叠加
\begin{equation}\text{loss} = -\sum_{t=1}^L \sum_{i=1}^N \lambda_i \log p_t^{(i)}[w_t]\end{equation}
训练完成后，我们只用$E$和$M$做常规的解码操作（比如Beam Search），也就是只用$h_t^{(1)}$而不需要$h_t^{(2)},h_t^{(3)},\cdots$了。这个流程就是本文的主角TeaForN了。

效果、思考与讨论 #

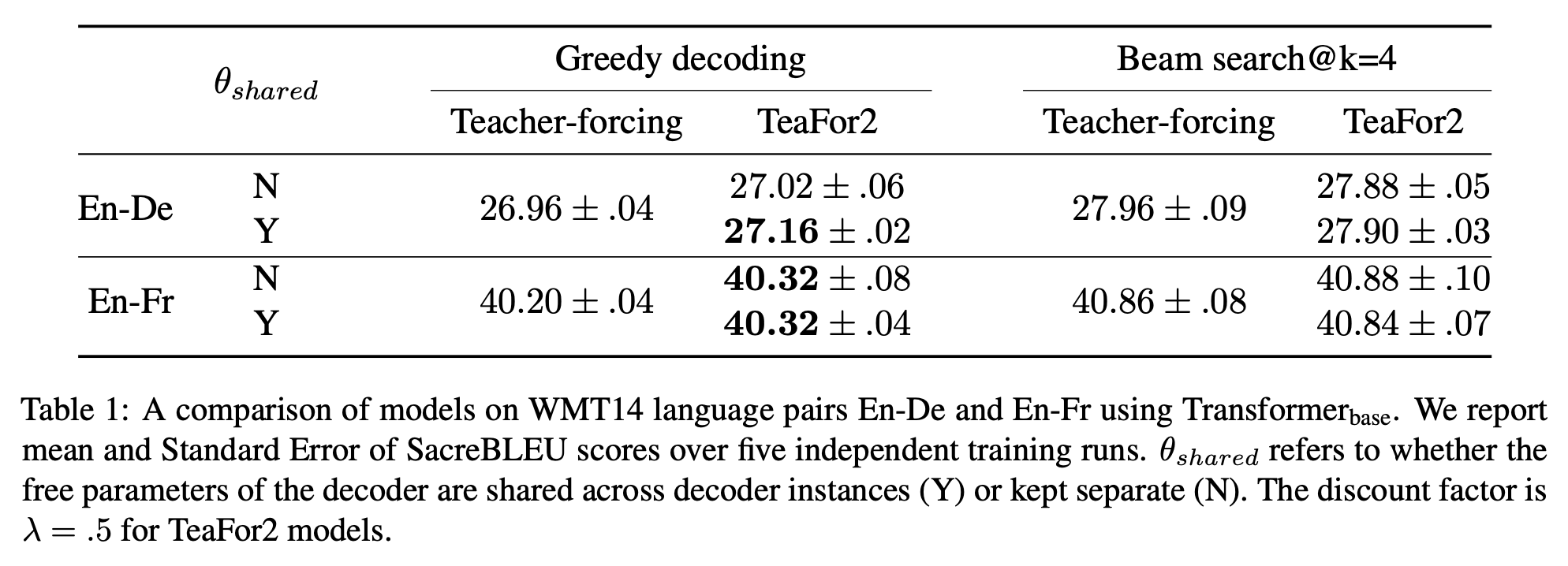
至于实验效果，自然是有提升的，从原论文的实验表格来看，在beam_size比较大时提升比较明显。其实也不难理解，按道理来说，这样处理后再不济应该也不会下降，因此算是一种“稳赚不赔”的策略了。

原论文讨论了几个值得商榷的点，我们这里也来看下。

首先，模型每一步迭代所用的$M$该不该共享权重？直觉来想共享是更好的，如果不共享权重，那么往前看$N$步，那么参数量就差不多是原来的$N$倍了，感觉是不大好。当然最好还是靠实验实验，原论文确实做了这个比较，证实了我们的直觉。

其次，可能最主要的疑问是：在迭代过程中将$[h_1, h_2, h_3, \cdots, h_{L-1}]$当作$[e_1, e_2, e_3, \cdots, e_{L-1}]$用是否真的靠谱？当然，实验结果已经表明了是可行的，这就是最有说服力的论据了。但由于$h_t$到$p_t$是通过内积来构建的，所以$h_t$跟$e_t$未必相似，如果能让它们更接近些，效果会不会更好？原论文考虑了如下的方式：
\begin{equation}\frac{\sum\limits_{w\in \text{Top}_k(p_t)}p_t[w] e_w}{\sum\limits_{w\in \text{Top}_k(p_t)}p_t[w]}\end{equation}
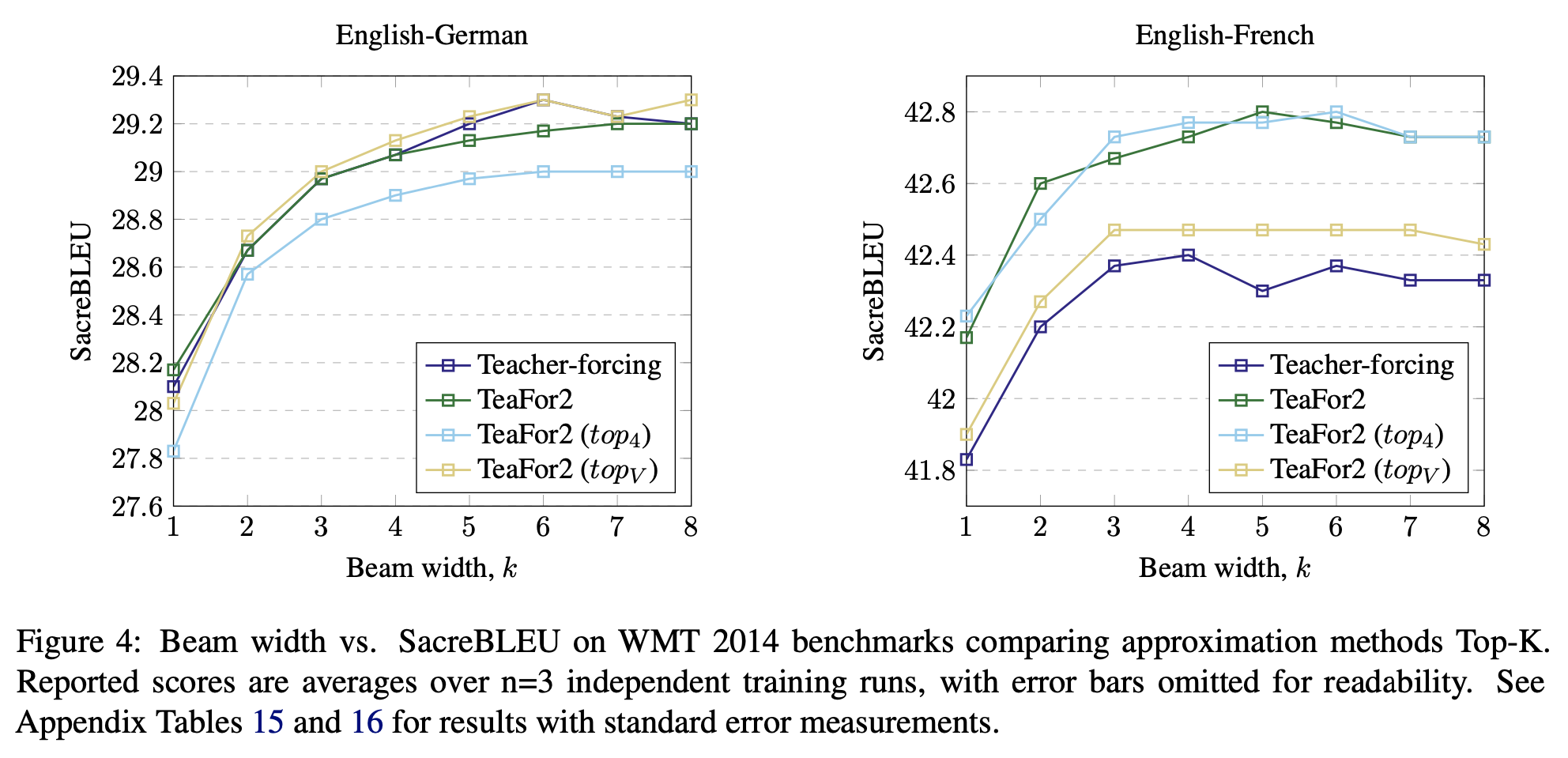
也就是说，每一步算出$p_t$后，取概率最大的$k$个token，将它们的Embedding向量加权平均来作为下一步迭代的输入。原论文实验了$k=4$和$k=|V|$（词表大小），结果如下图。总的来说Topk的效果不大稳定，好的情况也跟直接用$h_t$差不多，因此就没必要尝试别的了。

当然，我觉得要是论文再比较一下通过Gumbel Softmax来模拟采样效果就更加完美了。

来自文末的总结 #

本文分享了Google新提出来一种称为TeaForN的训练方式，它介乎Teacher Forcing和Student Forcing之间，能缓解模型的Exposure Bias问题，并且不用严重牺牲模型训练的并行性，是一种值得尝试的策略。除此之外，它实际上还提供了一种解决此类问题的新思想（通过迭代保持并行和前瞻），其中颇有值得回味的地方。

转载到请包括本文地址：https://kexue.fm/archives/7818

更详细的转载事宜请参考：《科学空间FAQ》