我们真的需要把训练集的损失降低到零吗？

在训练模型的时候，我们需要损失函数一直训练到0吗？显然不用。一般来说，我们是用训练集来训练模型，但希望的是验证集的损失越小越好，而正常来说训练集的损失降低到一定值后，验证集的损失就会开始上升，因此没必要把训练集的损失降低到0。

既然如此，在已经达到了某个阈值之后，我们可不可以做点别的事情来提升模型性能呢？ICML 2020的论文《Do We Need Zero Training Loss After Achieving Zero Training Error?》回答了这个问题。不过论文的回答也仅局限在“是什么”这个层面上，并没很好地描述“为什么”，另外看了知乎上kid丶大佬的解读，也没找到自己想要的答案。因此自己分析了一下，记录在此。

思路描述 #

论文提供的解决方案非常简单，假设原来的损失函数是$\mathcal{L}(\theta)$，现在改为$\tilde{\mathcal{L}}(\theta)$：
\begin{equation}\tilde{\mathcal{L}}(\theta)=|\mathcal{L}(\theta) - b|+b\end{equation}
其中$b$是预先设定的阈值。当$\mathcal{L}(\theta) > b$时$\tilde{\mathcal{L}}(\theta)=\mathcal{L}(\theta)$，这时候就是执行普通的梯度下降；而$\mathcal{L}(\theta) < b$时$\tilde{\mathcal{L}}(\theta)=2b-\mathcal{L}(\theta)$，注意到损失函数变号了，所以这时候是梯度上升。因此，总的来说就是以$b$为阈值，低于阈值时反而希望损失函数变大。论文把这个改动称为“Flooding”。

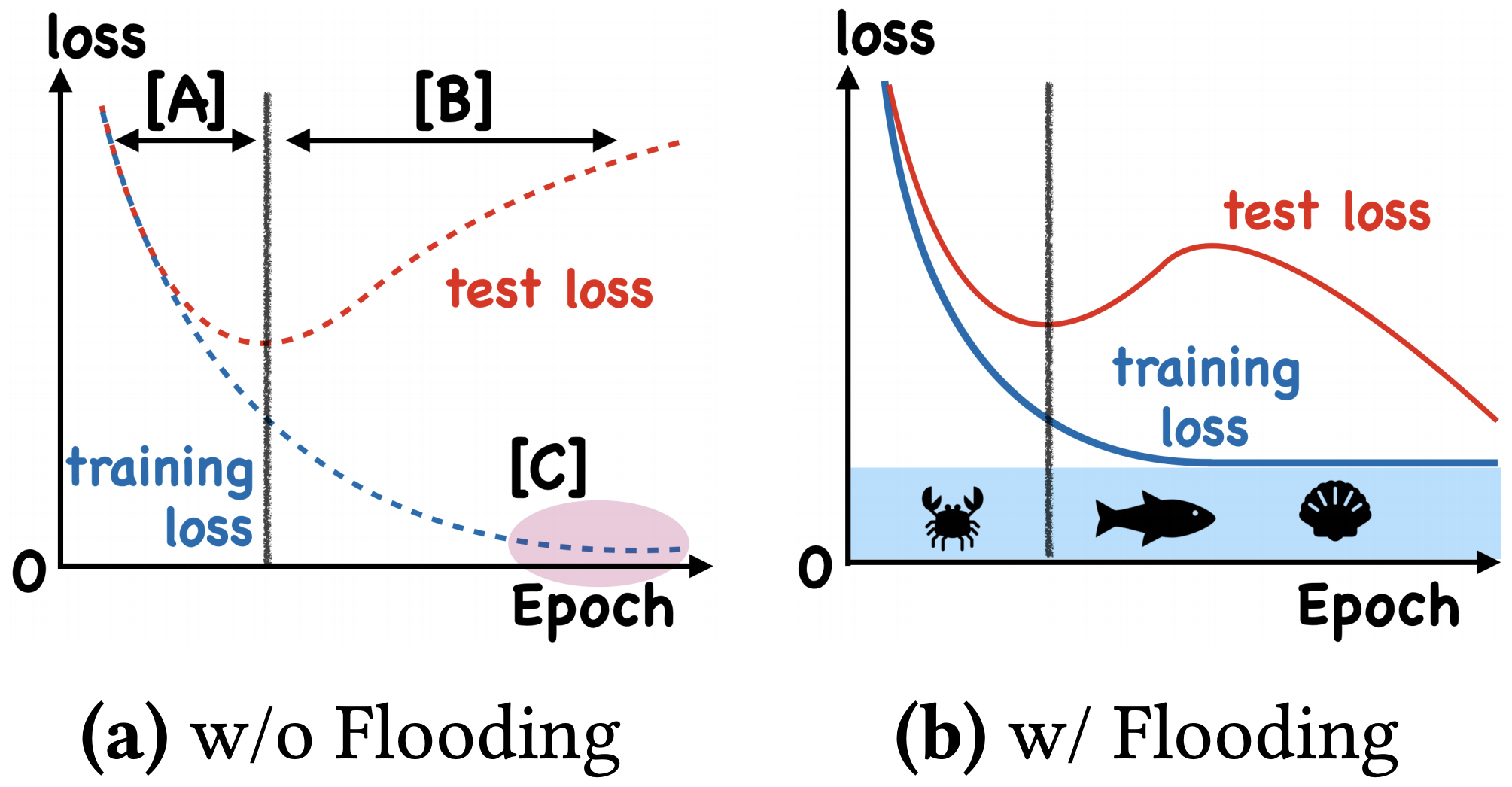
这样做有什么效果呢？论文显示，在某些任务中，训练集的损失函数经过这样处理后，验证集的损失能出现“二次下降（Double Descent）”，如下图：

简单来说，就是最终的验证集效果可能更好些，原论文的实验结果如下：

个人分析 #

如何解释这个方法呢？可以想象，当损失函数达到$b$之后，训练流程大概就是在交替执行梯度下降和梯度上升。直观想的话，感觉一步上升一步下降，似乎刚好抵消了。事实真的如此吗？我们来算一下看看。假设先下降一步后上升一步，学习率为$\varepsilon$，那么：
\begin{equation}\begin{aligned}&\theta_n = \theta_{n-1} - \varepsilon g(\theta_{n-1})\\
&\theta_{n+1} = \theta_n + \varepsilon g(\theta_n)
\end{aligned}\end{equation}
其中$g(\theta)=\nabla_{\theta}\mathcal{L}(\theta)$，现在我们有
\begin{equation}\begin{aligned}\theta_{n+1} =&\, \theta_{n-1} - \varepsilon g(\theta_{n-1}) + \varepsilon g\big(\theta_{n-1} - \varepsilon g(\theta_{n-1})\big)\\
\approx&\,\theta_{n-1} - \varepsilon g(\theta_{n-1}) + \varepsilon \big(g(\theta_{n-1}) - \varepsilon \nabla_{\theta} g(\theta_{n-1}) g(\theta_{n-1})\big)\\
=&\,\theta_{n-1} - \frac{\varepsilon^2}{2}\nabla_{\theta}\Vert g(\theta_{n-1})\Vert^2
\end{aligned}\end{equation}
近似那一步是使用了泰勒展式对损失函数进行近似展开，最终的结果就是相当于损失函数为梯度惩罚$\Vert g(\theta)\Vert^2=\Vert\nabla_{\theta}\mathcal{L}(\theta)\Vert^2$、学习率为$\frac{\varepsilon^2}{2}$的梯度下降。更妙的是，改为“先上升再下降”，其表达式依然是一样的（这不禁让我想起“先升价10%再降价10%”和“先降价10%再升价10%”的故事）。因此，平均而言，Flooding对损失函数的改动，相当于在保证了损失函数足够小之后去最小化$\Vert\nabla_{\theta}\mathcal{L}(\theta)\Vert^2$，也就是推动参数往更平稳的区域走，这通常能提供提高泛化性能（更好地抵抗扰动），因此一定程度上就能解释Flooding其作用的原因了。

本质上来讲，这跟往参数里边加入随机扰动、对抗训练等也没什么差别，只不过这里是保证了损失足够小后再加扰动。读者可以参考《泛化性乱弹：从随机噪声、梯度惩罚到虚拟对抗训练》了解相关内容，也可以参考“圣经”《深度学习》第二部分第七章的“正则化”一节。

继续脑洞 #

有心使用这个方法的读者可能会纠结于$b$的选择，不过笔者倒是有另外一个脑洞：$b$无非就是决定什么时候开始交替训练罢了，如果从一开始就用不同的学习率进行交替训练呢？也就是自始至终都执行
\begin{equation}\begin{aligned}&\theta_n = \theta_{n-1} - \varepsilon_1 g(\theta_{n-1})\\
&\theta_{n+1} = \theta_n + \varepsilon_2 g(\theta_n)
\end{aligned}\end{equation}
其中$\varepsilon_1 > \varepsilon_2$，这样我们就把$b$去掉了（当然引入了$\varepsilon_1/\varepsilon_2$的选择，天下没免费午餐）。重复上述近似展开，我们就得到
\begin{equation}\begin{aligned}
\theta_{n+1} \approx&\, \theta_{n-1} - (\varepsilon_1 - \varepsilon_2) g(\theta_{n-1}) - \frac{\varepsilon_1\varepsilon_2}{2}\nabla_{\theta}\Vert g(\theta_{n-1})\Vert^2\\
=&\,\theta_{n-1} - (\varepsilon_1 - \varepsilon_2)\nabla_{\theta}\left[\mathcal{L}(\theta_{n-1}) + \frac{\varepsilon_1\varepsilon_2}{2(\varepsilon_1 - \varepsilon_2)}\Vert \nabla_{\theta}\mathcal{L}(\theta_{n-1})\Vert^2\right]
\end{aligned}\end{equation}
这就相当于自始至终都在用学习率$\varepsilon_1 - \varepsilon_2$来优化损失函数$\mathcal{L}(\theta) + \frac{\varepsilon_1\varepsilon_2}{2(\varepsilon_1 - \varepsilon_2)}\Vert\nabla_{\theta}\mathcal{L}(\theta)\Vert^2$了，也就是说一开始就把梯度惩罚给加了进去。这样能提升模型的泛化性能吗？笔者简单试了一下，有些情况下会有轻微的提升，基本上都不会有负面影响，总的来说不如自己直接加梯度惩罚好，所以不建议这样做。

注：读者@xx205提供了参考文献《Backstitch: Counteracting Finite-sample Bias via Negative Steps》，里边指出这种做法在语音识别上是有效的，所以笔者的上述说法可能也不尽完善，请读者自行测试甄别。再次感谢读者读者@xx205提供的资料。

文章小结 #

本文简单介绍了ICML 2020一篇论文提出的“到一定程度后就梯度上升”的训练策略，并给出了自己的推导和理解，结果显示它相当于对参数的梯度惩罚，而梯度惩罚也是常见的正则化手段之一。

转载到请包括本文地址：https://kexue.fm/archives/7643

更详细的转载事宜请参考：《科学空间FAQ》