低秩近似之路(四):ID
By 苏剑林 | 2024-10-30 | 19333位读者 | 引用这篇文章的主角是ID(Interpolative Decomposition),中文可以称之为“插值分解”,它同样可以理解为是一种具有特定结构的低秩分解,其中的一侧是该矩阵的若干列(当然如果你偏好于行,那么选择行也没什么问题),换句话说,ID试图从一个矩阵中找出若干关键列作为“骨架”(通常也称作“草图”)来逼近原始矩阵。
可能很多读者都未曾听说过ID,即便维基百科也只有几句语焉不详的介绍(链接),但事实上,ID跟SVD一样早已内置在SciPy之中(参考scipy.linalg.interpolative),这侧面印证了ID的实用价值。
基本定义
前三篇文章我们分别介绍了伪逆、SVD、CR近似,它们都可以视为寻找特定结构的低秩近似:
\begin{equation}\mathop{\text{argmin}}_{\text{rank}(\tilde{\boldsymbol{M}})\leq r}\Vert \tilde{\boldsymbol{M}} - \boldsymbol{M}\Vert_F^2\end{equation}
让MathJax的数学公式随窗口大小自动缩放
By 苏剑林 | 2024-10-15 | 16476位读者 | 引用随着MathJax的出现和流行,在网页上显示数学公式便逐渐有了标准答案。然而,MathJax(包括其竞品KaTeX)只是负责将网页LaTeX代码转化为数学公式,对于自适应分辨率方面依然没有太好的办法。像本站一些数学文章,因为是在PC端排版好的,所以在PC端浏览效果尚可,但转到手机上看就可能有点难以入目了。
经过测试,笔者得到了一个方案,让MathJax的数学公式也能像图片一样,随着窗口大小而自适应缩放,从而尽量保证移动端的显示效果,在此跟大家分享一波。
背景思路
这个问题的起源是,即便在PC端进行排版,有时候也会遇到一些单行公式的长度超出了网页宽度,但又不大好换行的情况,这时候一个解决方案是用HTML代码手动调整一下公式的字体大小,比如
<span style="font-size:90%">
\begin{equation}一个超长的数学公式\end{equation}
</span>VQ的旋转技巧:梯度直通估计的一般推广
By 苏剑林 | 2024-10-24 | 24276位读者 | 引用随着多模态LLM的方兴未艾,VQ(Vector Quantization)的地位也“水涨船高”,它可以作为视觉乃至任意模态的Tokenizer,将多模态数据统一到自回归生成框架中。遗憾的是,自VQ-VAE首次提出VQ以来,其理论并没有显著进步,像编码表的坍缩或利用率低等问题至今仍亟待解决,取而代之的是FSQ等替代方案被提出,成为了VQ有力的“竞争对手”。
然而,FSQ并不能在任何场景下都替代VQ,所以VQ本身的改进依然是有价值的。近日笔者读到了《Restructuring Vector Quantization with the Rotation Trick》,它提出了一种旋转技巧,声称能改善VQ的一系列问题,本文就让我们一起来品鉴一下。
回顾
早在五年前的博文《VQ-VAE的简明介绍:量子化自编码器》中我们就介绍过了VQ-VAE,后来在《简单得令人尴尬的FSQ:“四舍五入”超越了VQ-VAE》介绍FSQ的时候,也再次仔细地温习了VQ-VAE,还不了解的读者可以先阅读这两篇文章。
从Hessian近似看自适应学习率优化器
By 苏剑林 | 2024-11-29 | 13689位读者 | 引用这几天在重温去年的Meta的一篇论文《A Theory on Adam Instability in Large-Scale Machine Learning》,里边给出了看待Adam等自适应学习率优化器的新视角:它指出梯度平方的滑动平均某种程度上近似于在估计Hessian矩阵的平方,从而Adam、RMSprop等优化器实际上近似于二阶的Newton法。
这个角度颇为新颖,而且表面上跟以往的一些Hessian近似有明显的差异,因此值得我们去学习和思考一番。
牛顿下降
设损失函数为$\mathcal{L}(\boldsymbol{\theta})$,其中待优化参数为$\boldsymbol{\theta}$,我们的优化目标是
\begin{equation}\boldsymbol{\theta}^* = \mathop{\text{argmin}}_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})\label{eq:loss}\end{equation}
假设$\boldsymbol{\theta}$的当前值是$\boldsymbol{\theta}_t$,Newton法通过将损失函数展开到二阶来寻求$\boldsymbol{\theta}_{t+1}$:
\begin{equation}\mathcal{L}(\boldsymbol{\theta})\approx \mathcal{L}(\boldsymbol{\theta}_t) + \boldsymbol{g}_t^{\top}(\boldsymbol{\theta} - \boldsymbol{\theta}_t) + \frac{1}{2}(\boldsymbol{\theta} - \boldsymbol{\theta}_t)^{\top}\boldsymbol{\mathcal{H}}_t(\boldsymbol{\theta} - \boldsymbol{\theta}_t)\end{equation}
Adam的epsilon如何影响学习率的Scaling Law?
By 苏剑林 | 2024-11-18 | 17312位读者 | 引用上一篇文章《当Batch Size增大时,学习率该如何随之变化?》我们从多个角度讨论了学习率与Batch Size之间的缩放规律,其中对于Adam优化器我们采用了SignSGD近似,这是分析Adam优化器常用的手段。那么一个很自然的问题就是:用SignSGD来近似Adam究竟有多科学呢?
我们知道,Adam优化器的更新量分母会带有一个$\epsilon$,初衷是预防除零错误,所以其值通常很接近于零,以至于我们做理论分析的时候通常选择忽略掉它。然而,当前LLM的训练尤其是低精度训练,我们往往会选择偏大的$\epsilon$,这导致在训练的中、后期$\epsilon$往往已经超过梯度平方大小,所以$\epsilon$的存在事实上已经不可忽略。
因此,这篇文章我们试图探索$\epsilon$如何影响Adam的学习率与Batch Size的Scaling Law,为相关问题提供一个参考的计算方案。
生成扩散模型漫谈(二十六):基于恒等式的蒸馏(下)
By 苏剑林 | 2024-11-22 | 18423位读者 | 引用继续回到我们的扩散系列。在《生成扩散模型漫谈(二十五):基于恒等式的蒸馏(上)》中,我们介绍了SiD(Score identity Distillation),这是一种不需要真实数据、也不需要从教师模型采样的扩散模型蒸馏方案,其形式类似GAN,但有着比GAN更好的训练稳定性。
SiD的核心是通过恒等变换来为学生模型构建更好的损失函数,这一点是开创性的,同时也遗留了一些问题。比如,SiD对损失函数的恒等变换是不完全的,如果完全变换会如何?如何从理论上解释SiD引入的$\lambda$的必要性?上个月放出的《Flow Generator Matching》(简称FGM)成功从更本质的梯度角度解释了$\lambda=0.5$的选择,而受到FGM启发,笔者则进一步发现了$\lambda = 1$的一种解释。
接下来我们将详细介绍SiD的上述理论进展。
Muon优化器赏析:从向量到矩阵的本质跨越
By 苏剑林 | 2024-12-10 | 13665位读者 | 引用随着LLM时代的到来,学术界对于优化器的研究热情似乎有所减退。这主要是因为目前主流的AdamW已经能够满足大多数需求,而如果对优化器“大动干戈”,那么需要巨大的验证成本。因此,当前优化器的变化,多数都只是工业界根据自己的训练经验来对AdamW打的一些小补丁。
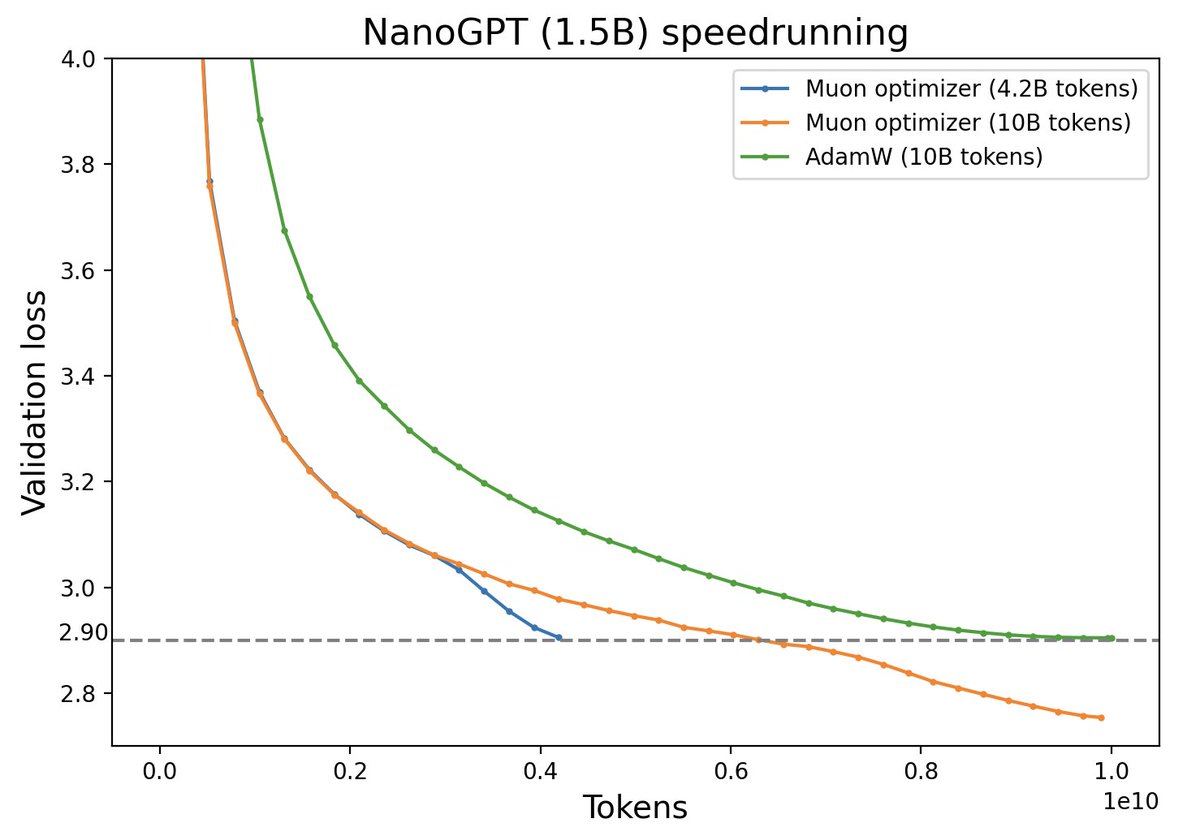
不过,最近推特上一个名为“Muon”的优化器颇为热闹,它声称比AdamW更为高效,且并不只是在Adam基础上的“小打小闹”,而是体现了关于向量与矩阵差异的一些值得深思的原理。本文让我们一起赏析一番。
生成扩散模型漫谈(二十七):将步长作为条件输入
By 苏剑林 | 2024-12-15 | 10317位读者 | 引用这篇文章我们再次聚焦于扩散模型的采样加速。众所周知,扩散模型的采样加速主要有两种思路,一是开发更高效的求解器,二是事后蒸馏。然而,据笔者观察,除了上两篇文章介绍过的SiD外,这两种方案都鲜有能将生成步数降低到一步的结果。虽然SiD能做到单步生成,但它需要额外的蒸馏成本,并且蒸馏过程中用到了类似GAN的交替训练过程,总让人感觉差点意思。
本文要介绍的是《One Step Diffusion via Shortcut Models》,其突破性思想是将生成步长也作为扩散模型的条件输入,然后往训练目标中加入了一个直观的正则项,这样就能直接稳定训练出可以单步生成模型,可谓简单有效的经典之作。
ODE扩散
原论文的结论是基于ODE式扩散模型的,而对于ODE式扩散的理论基础,我们在本系列的(六)、(十二)、(十四)、(十五)、(十七)等博客中已经多次介绍,其中最简单的一种理解方式大概是(十七)中的ReFlow视角,下面我们简单重复一下。








最近评论