再谈类别不平衡问题:调节权重与魔改Loss的对比联系
By 苏剑林 | 2020-08-31 | 84692位读者 | 引用类别不平衡问题,也称为长尾分布问题,在本博客里已经有好几次相关讨论了,比如《从loss的硬截断、软化到focal loss》、《将“Softmax+交叉熵”推广到多标签分类问题》、《通过互信息思想来缓解类别不平衡问题》。对于缓解类别不平衡,比较基本的方法就是调节样本权重,看起来“高端”一点的方法则是各种魔改loss了(比如Focal Loss、Dice Loss、Logits Adjustment等),本文希望比较系统地理解一下它们之间的联系。
从光滑准确率到交叉熵
这里的分析主要以sigmoid的2分类为主,但多数结论可以平行推广到softmax的多分类。设$x$为输入,$y\in\{0,1\}$为目标,$p_{\theta}(x) \in [0, 1]$为模型。理想情况下,当然是要评测什么指标,我们就去优化那个指标。对于分类问题来说,最朴素的指标当然就是准确率,但准确率并没有办法提供有效的梯度,所以不能直接来训练。
搜狐文本匹配:基于条件LayerNorm的多任务baseline
By 苏剑林 | 2021-04-16 | 96009位读者 | 引用前段时间看到了“2021搜狐校园文本匹配算法大赛”,觉得赛题颇有意思,便尝试了一下,不过由于比赛本身只是面向在校学生,所以笔者是不能作为正式参赛人员参赛的,因此把自己的做法开源出来,作为比赛baseline供大家参考。
赛题介绍
顾名思义,比赛的任务是文本匹配,即判断两个文本是否相似,本来是比较常规的任务,但有意思的是它分了多个子任务。具体来说,它分A、B两大类,A类匹配标准宽松一些,B类匹配标准严格一些,然后每个大类下又分为“短短匹配”、“短长匹配”、“长长匹配”3个小类,因此,虽然任务类型相同,但严格来看它是六个不同的子任务。
必须要GPT3吗?不,BERT的MLM模型也能小样本学习
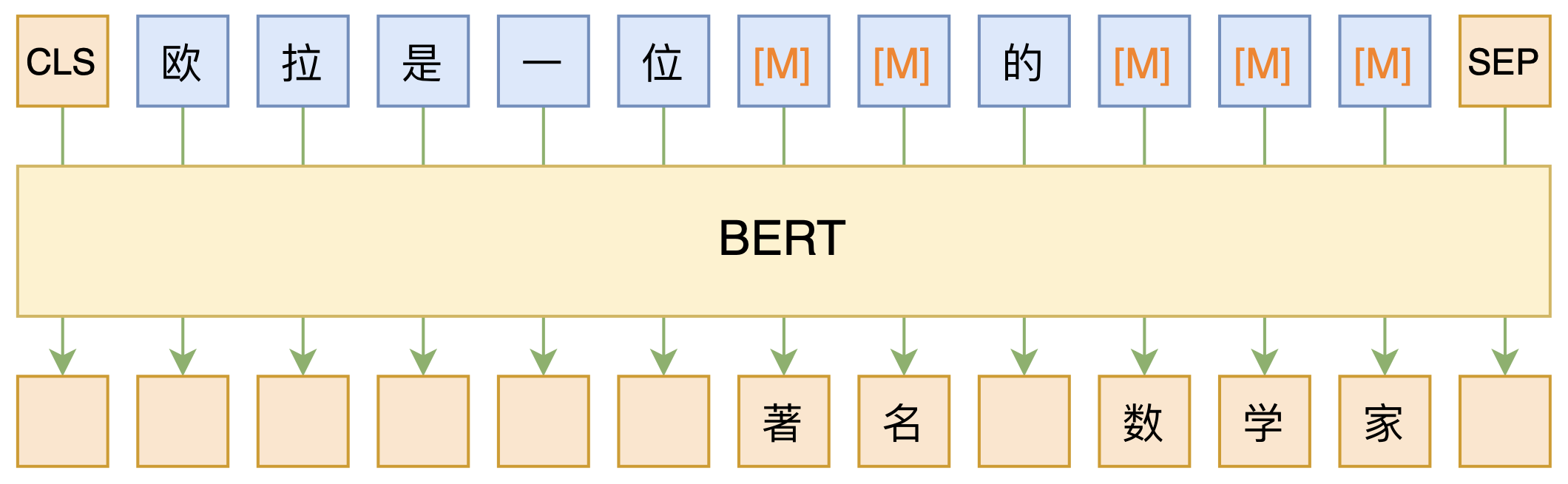
By 苏剑林 | 2020-09-27 | 162219位读者 | 引用大家都知道现在GPT3风头正盛,然而,到处都是GPT3、GPT3地推,读者是否记得GPT3论文的名字呢?事实上,GPT3的论文叫做《Language Models are Few-Shot Learners》,标题里边已经没有G、P、T几个单词了,只不过它跟开始的GPT是一脉相承的,因此还是以GPT称呼它。顾名思义,GPT3主打的是Few-Shot Learning,也就是小样本学习。此外,GPT3的另一个特点就是大,最大的版本多达1750亿参数,是BERT Base的一千多倍。
正因如此,前些天Arxiv上的一篇论文《It's Not Just Size That Matters: Small Language Models Are Also Few-Shot Learners》便引起了笔者的注意,意译过来就是“谁说一定要大的?小模型也可以做小样本学习”。显然,这标题对标的就是GPT3,于是笔者饶有兴趣地点进去看看是谁这么有勇气挑战GPT3,又是怎样的小模型能挑战GPT3?经过阅读,原来作者提出通过适当的构造,用BERT的MLM模型也可以做小样本学习,看完之后颇有一种“原来还可以这样做”的恍然大悟感~在此与大家分享一下。
从动力学角度看优化算法(五):为什么学习率不宜过小?
By 苏剑林 | 2020-10-10 | 58811位读者 | 引用本文的主题是“为什么我们需要有限的学习率”,所谓“有限”,指的是不大也不小,适中即可,太大容易导致算法发散,这不难理解,但为什么太小也不好呢?一个容易理解的答案是,学习率过小需要迭代的步数过多,这是一种没有必要的浪费,因此从“节能”和“加速”的角度来看,我们不用过小的学习率。但如果不考虑算力和时间,那么过小的学习率是否可取呢?Google最近发布在Arxiv上的论文《Implicit Gradient Regularization》试图回答了这个问题,它指出有限的学习率隐式地给优化过程带来了梯度惩罚项,而这个梯度惩罚项对于提高泛化性能是有帮助的,因此哪怕不考虑算力和时间等因素,也不应该用过小的学习率。
对于梯度惩罚,本博客已有过多次讨论,在文章《对抗训练浅谈:意义、方法和思考(附Keras实现)》和《泛化性乱弹:从随机噪声、梯度惩罚到虚拟对抗训练》中,我们就分析了对抗训练一定程度上等价于对输入的梯度惩罚,而文章《我们真的需要把训练集的损失降低到零吗?》介绍的Flooding技巧则相当于对参数的梯度惩罚。总的来说,不管是对输入还是对参数的梯度惩罚,都对提高泛化能力有一定帮助。
BERT可以上几年级了?Seq2Seq“硬刚”小学数学应用题
By 苏剑林 | 2020-10-19 | 73341位读者 | 引用“盈亏问题”、“年龄问题”、“植树问题”、“牛吃草问题”、“利润问题”...,小学阶段你是否曾被各种花样的数学应用题折磨过呢?没关系,现在机器学习模型也可以帮助我们去解答应用题了,来看看它可以上几年级了?
本文将给出一个求解小学数学应用题(Math Word Problem)的baseline,基于ape210k数据集训练,直接用Seq2Seq模型生成可执行的数学表达式,最终Large版本的模型能达到75%的准确率,明显高于ape210k论文所报告的结果。所谓“硬刚”,指的是没有对表达式做特别的转换,也没有通过模板处理,就直接生成跟人类做法相近的可读表达式。
TeaForN:让Teacher Forcing更有“远见”一些
By 苏剑林 | 2020-10-27 | 43443位读者 | 引用Teacher Forcing是Seq2Seq模型的经典训练方式,而Exposure Bias则是Teacher Forcing的经典缺陷,这对于搞文本生成的同学来说应该是耳熟能详的事实了。笔者之前也曾写过博文《Seq2Seq中Exposure Bias现象的浅析与对策》,初步地分析过Exposure Bias问题。
本文则介绍Google新提出的一种名为“TeaForN”的缓解Exposure Bias现象的方案,来自论文《TeaForN: Teacher-Forcing with N-grams》,它通过嵌套迭代的方式,让模型能提前预估到后$N$个token(而不仅仅是当前要预测的token),其处理思路上颇有可圈可点之处,值得我们学习。
(注:为了尽量跟本博客旧文章保持一致,本文的记号与原论文的记号有所不同,请大家以理解符号含义为主,不要强记符号形式。)
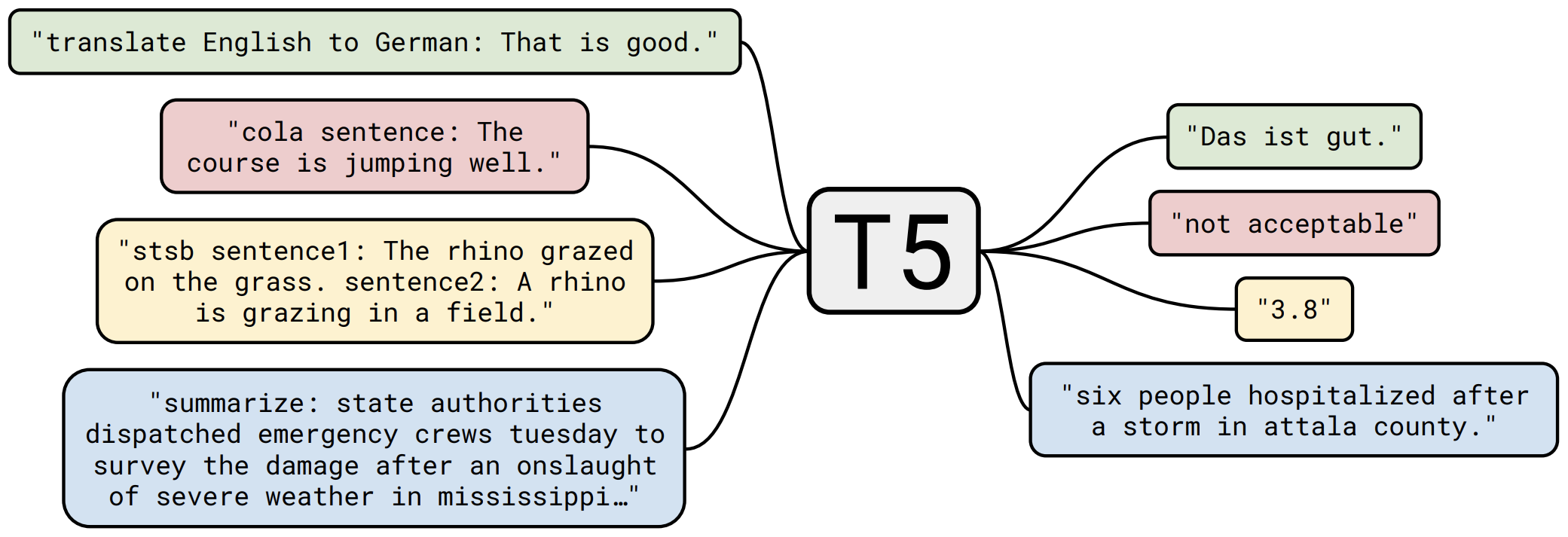
那个屠榜的T5模型,现在可以在中文上玩玩了
By 苏剑林 | 2020-11-06 | 139399位读者 | 引用不知道大家对Google去年的屠榜之作T5还有没有印象?就是那个打着“万事皆可Seq2Seq”的旗号、最大搞了110亿参数、一举刷新了GLUE、SuperGLUE等多个NLP榜单的模型,而且过去一年了,T5仍然是SuperGLUE榜单上的第一,目前还稳妥地拉开着第二名2%的差距。然而,对于中文界的朋友来说,T5可能没有什么存在感,原因很简单:没有中文版T5可用。不过这个现状要改变了,因为Google最近放出了多国语言版的T5(mT5),里边当然是包含了中文语言。虽然不是纯正的中文版,但也能凑合着用一下。
本文将会对T5模型做一个简单的回顾与介绍,然后再介绍一下如何在bert4keras中调用mT5模型来做中文任务。作为一个原生的Seq2Seq预训练模型,mT5在文本生成任务上的表现还是相当不错的,非常值得一试。
当GPT遇上中国象棋:写过文章解过题,要不再来下盘棋?
By 苏剑林 | 2020-11-11 | 58880位读者 | 引用不知道读者有没有看过量子位年初的文章《最强写作AI竟然学会象棋和作曲,语言模型跨界操作引热议,在线求战》,里边提到有网友用GPT2模型训练了一个下国际象棋的模型。笔者一直在想,这么有趣的事情怎么可以没有中文版呢?对于国际象棋来说,其中文版自然就是中国象棋了,于是我一直有想着把它的结果在中国象棋上面复现一下。拖了大半年,在最近几天终于把这个事情完成了,在此跟大家分享一下。
象棋谱式
将军不离九宫内,士止相随不出官。
象飞四方营四角,马行一步一尖冲。
炮须隔子打一子,车行直路任西东。
唯卒只能行一步,过河横进退无踪。











最近评论