Mitchell近似:乘法变为加法,误差不超过1/9
By 苏剑林 | 2020-12-14 | 57463位读者 | Kimi 引用今天给大家介绍一篇1962年的论文《Computer Multiplication and Division Using Binary Logarithms》,作者是John N. Mitchell,他在里边提出了一个相当有意思的算法:在二进制下,可以完全通过加法来近似完成两个数的相乘,最大误差不超过1/9。整个算法相当巧妙,更有意思的是它还有着非常简洁的编程实现,让人拍案叫绝。然而,笔者发现网上居然找不到介绍这个算法的网页,所以在此介绍一番。
你以为这只是过时的玩意?那你就错了,前不久才有人利用它发了一篇NeurIPS 2020呢!所以,确定不来了解一下吗?
从动力学角度看优化算法(六):为什么SimSiam不退化?
By 苏剑林 | 2020-12-11 | 126476位读者 | Kimi 引用自SimCLR以来,CV中关于无监督特征学习的工作层出不穷,让人眼花缭乱。这些工作大多数都是基于对比学习的,即通过适当的方式构造正负样本进行分类学习的。然而,在众多类似的工作中总有一些特立独行的研究,比如Google的BYOL和最近的SimSiam,它们提出了单靠正样本就可以完成特征学习的方案,让人觉得耳目一新。但是没有负样本的支撑,模型怎么不会退化(坍缩)为一个没有意义的常数模型呢?这便是这两篇论文最值得让人思考和回味的问题了。
其中SimSiam给出了让很多人都点赞的答案,但笔者觉得SimSiam也只是把问题换了种说法,并没有真的解决这个问题。笔者认为,像SimSiam、GAN等模型的成功,很重要的原因是使用了基于梯度的优化器(而非其他更强或者更弱的优化器),所以不结合优化动力学的答案都是不完整的。在这里,笔者尝试结合动力学来分析SimSiam不会退化的原因。
SimSiam
在看SimSiam之前,我们可以先看看BYOL,来自论文《Bootstrap your own latent: A new approach to self-supervised Learning》,其学习过程很简单,就是维护两个编码器Student和Teacher,其中Teacher是Student的滑动平均,Student则又反过来向Teacher学习,有种“左脚踩右脚”就可以飞起来的感觉。示意图如下:
【龟鱼记】全陶粒的同程底滤生态缸
By 苏剑林 | 2020-12-07 | 84315位读者 | Kimi 引用层次分解位置编码,让BERT可以处理超长文本
By 苏剑林 | 2020-12-04 | 181549位读者 | Kimi 引用大家都知道,目前的主流的BERT模型最多能处理512个token的文本。导致这一瓶颈的根本原因是BERT使用了从随机初始化训练出来的绝对位置编码,一般的最大位置设为了512,因此顶多只能处理512个token,多出来的部分就没有位置编码可用了。当然,还有一个重要的原因是Attention的$\mathcal{O}(n^2)$复杂度,导致长序列时显存用量大大增加,一般显卡也finetune不了。
本文主要面向前一个原因,即假设有足够多的显存前提下,如何简单修改当前最大长度为512的BERT模型,使得它可以直接处理更长的文本,主要思路是层次分解已经训练好的绝对位置编码,使得它可以延拓到更长的位置。
Performer:用随机投影将Attention的复杂度线性化
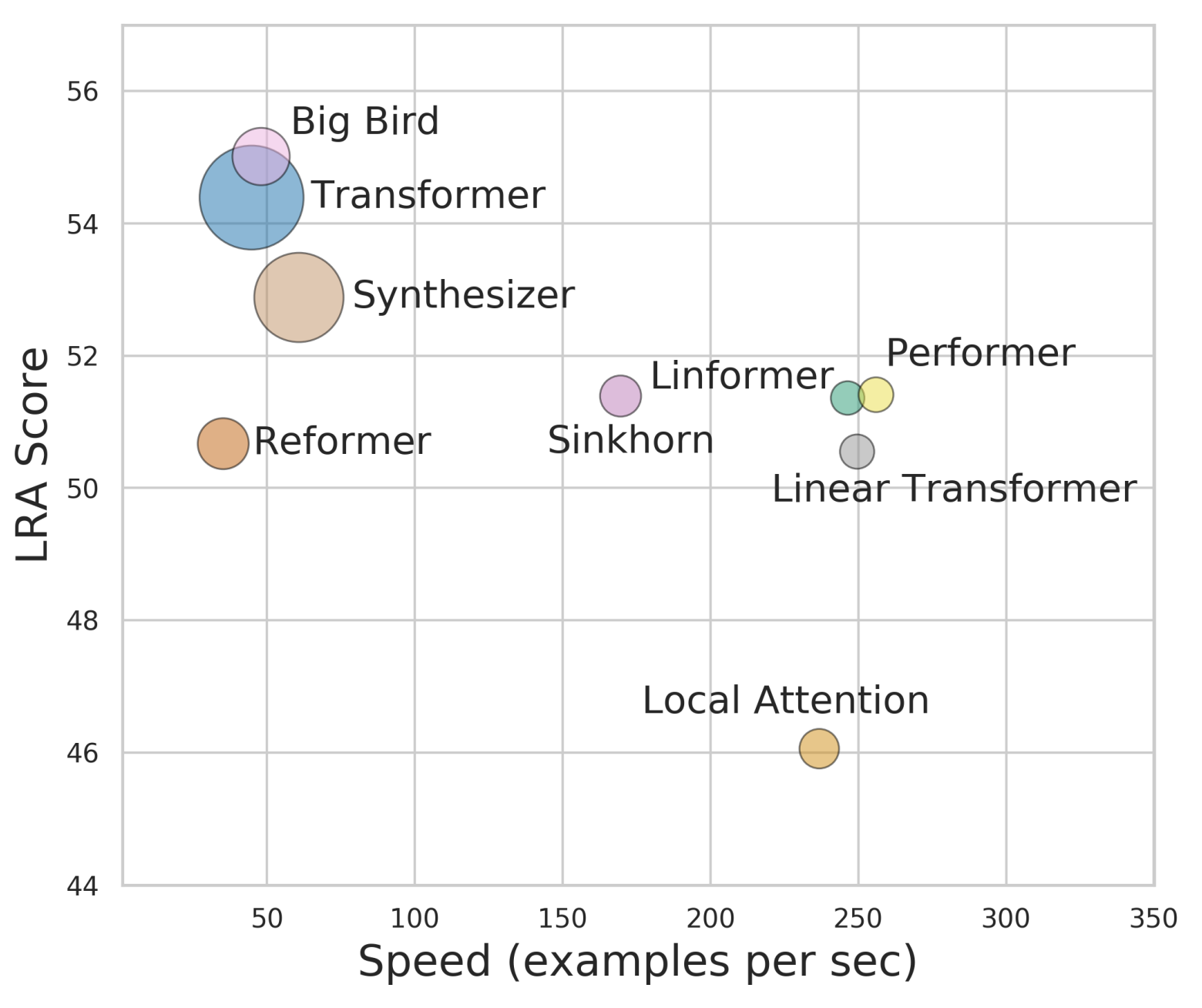
By 苏剑林 | 2020-12-01 | 116151位读者 | Kimi 引用Attention机制的$\mathcal{O}(n^2)$复杂度是一个老大难问题了,改变这一复杂度的思路主要有两种:一是走稀疏化的思路,比如我们以往介绍过的Sparse Attention以及Google前几个月搞出来的Big Bird,等等;二是走线性化的思路,这部分工作我们之前总结在《线性Attention的探索:Attention必须有个Softmax吗?》中,读者可以翻看一下。本文则介绍一项新的改进工作Performer,出自Google的文章《Rethinking Attention with Performers》,它的目标相当霸气:通过随机投影,在不损失精度的情况下,将Attention的复杂度线性化。
说直接点,就是理想情况下我们可以不用重新训练模型,输出结果也不会有明显变化,但是复杂度降到了$\mathcal{O}(n)$!看起来真的是“天上掉馅饼”般的改进了,真的有这么美好吗?
exp(x)在x=0处的偶次泰勒展开式总是正的
By 苏剑林 | 2020-11-24 | 47201位读者 | Kimi 引用刚看到一个有意思的结论:
对于任意实数$x$及偶数$n$,总有$\sum\limits_{k=0}^n \frac{x^k}{k!} > 0$,即$e^x$在$x=0$处的偶次泰勒展开式总是正的。
下面我们来看一下这个结论的证明,以及它在寻找softmax替代品中的应用。
证明过程
看上去这是一个很强的结果,证明会不会很复杂?其实证明非常简单,记
\begin{equation}f_n(x) = \sum\limits_{k=0}^n \frac{x^k}{k!}\end{equation}
当$n$是偶数时,我们有$\lim\limits_{x\to\pm\infty} f_n(x)=+\infty$,即整体是开口向上的,所以我们只需要证明它的最小值大于0就行了,又因为它是一个光滑连续的多项式函数,所以最小值点必然是某个极小值点。那么换个角度想,我们只需要证明它所有的极值点(不管是极大还是极小)所对应的函数值都大于0。
跟风玩玩目前最大的中文GPT2模型(bert4keras)
By 苏剑林 | 2020-11-20 | 94253位读者 | Kimi 引用相信不少读者这几天都看到了清华大学与智源人工智能研究院一起搞的“清源计划”(相关链接《中文版GPT-3来了?智源研究院发布清源 CPM —— 以中文为核心的大规模预训练模型》),里边开源了目前最大的中文GPT2模型CPM-LM(26亿参数),据说未来还会开源200亿甚至1000亿参数的模型,要打造“中文界的GPT3”。
我们知道,GPT3不需要finetune就可以实现Few Shot,而目前CPM-LM的演示例子中,Few Shot的效果也是相当不错的,让人跃跃欲试,笔者也不例外。既然要尝试,肯定要将它适配到自己的bert4keras中才顺手,于是适配工作便开始了。本以为这是一件很轻松的事情,谁知道踩坑踩了快3天才把它搞好,在此把踩坑与测试的过程稍微记录一下。
也来谈谈RNN的梯度消失/爆炸问题
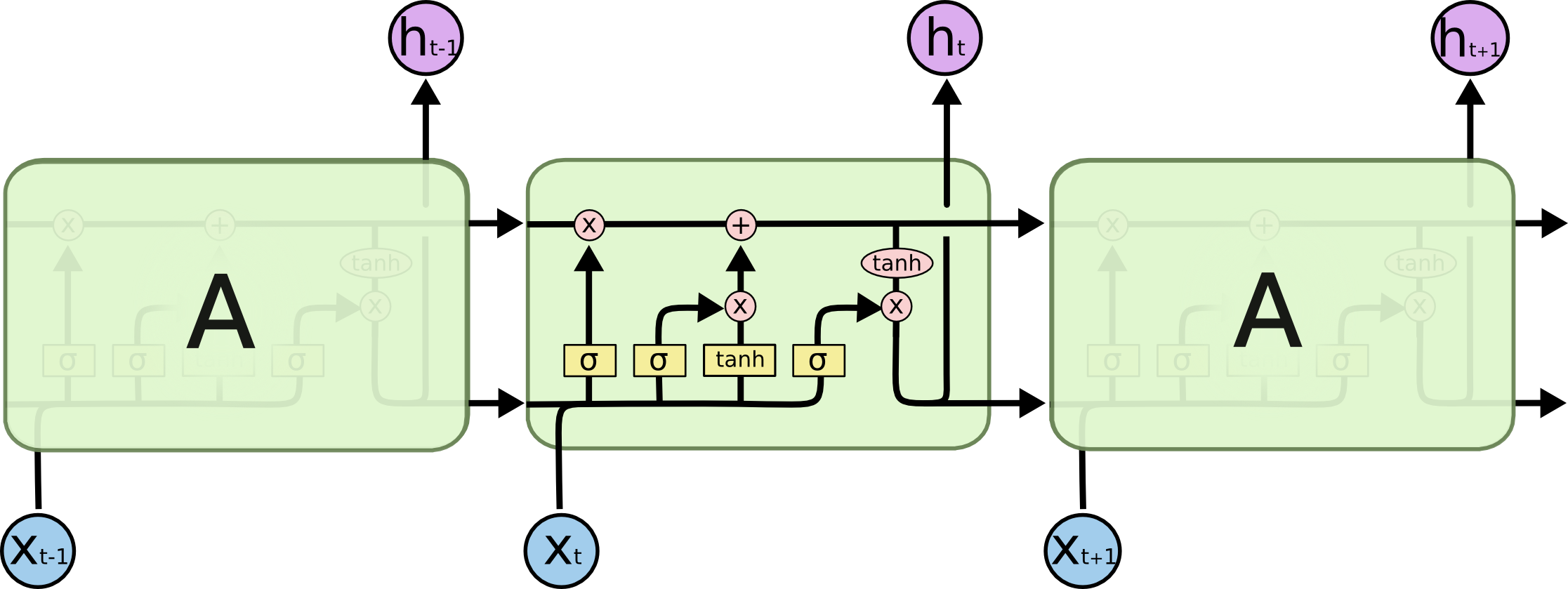
By 苏剑林 | 2020-11-13 | 124728位读者 | Kimi 引用尽管Transformer类的模型已经攻占了NLP的多数领域,但诸如LSTM、GRU之类的RNN模型依然在某些场景下有它的独特价值,所以RNN依然是值得我们好好学习的模型。而对于RNN梯度的相关分析,则是一个从优化角度思考分析模型的优秀例子,值得大家仔细琢磨理解。君不见,诸如“LSTM为什么能解决梯度消失/爆炸”等问题依然是目前流行的面试题之一...
关于此类问题,已有不少网友做出过回答,然而笔者查找了一些文章(包括知乎上的部分回答、专栏以及经典的英文博客),发现没有找到比较好的答案:有些推导记号本身就混乱不堪,有些论述过程没有突出重点,整体而言感觉不够清晰自洽。为此,笔者也尝试给出自己的理解,供大家参考。







 感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持!
感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持! 科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。
科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。 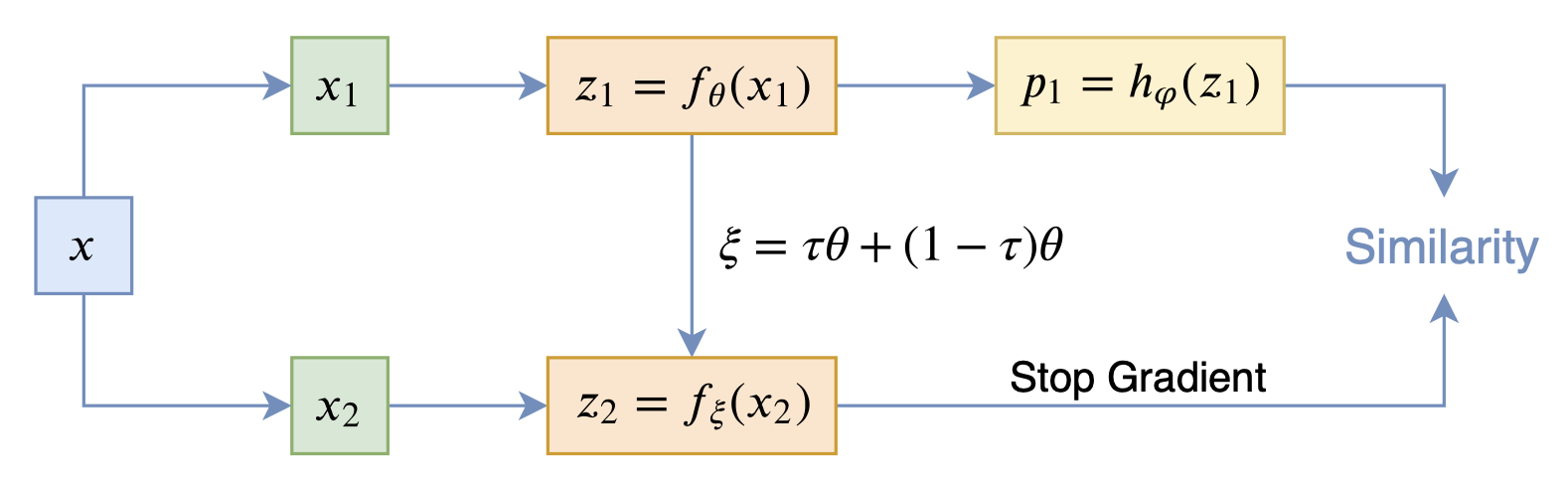



最近评论