关于行星留的周期的计算，我们之前已经讨论过这个问题，利用的是微积分的方法。也许不少还没有高数基础的朋友会感到很头晕，因此在这里给出一个从几何方面讨论的推导。

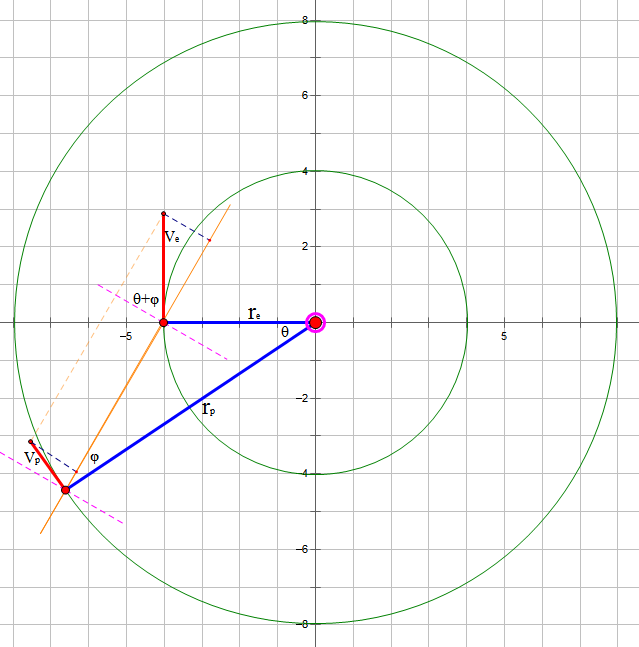
关于留，很多人认为就是行星相对于地球的速度为0的时刻，其实这个说法稍欠准确，严格来讲应该要将速度改为“角速度”或“切向速度”（天文的切向就是指与视线方向垂直的方向）。实际的运动中，没有哪一瞬间行星相对于地球的运动速度是为0的。根据这句话，我们可以作出下面的图（依旧只考虑正圆运动）：

行星留-运动分析

行星留-运动分析

并且列出：
$$V_p \cos\varphi=V_e \cos(\theta+\varphi)=V_e \cos\theta \cos \varphi-V_e \sin\theta \sin\varphi$$
即
$$V_p=V_e \cos \theta-V_e \tan \varphi \sin\theta$$
同时，根据图上可以列出
$tan\varphi=\frac{r_e sin\theta}{r_p-r_e cos\theta}$，代入上式得到
$$\begin{aligned}V_p(r_p-r_e \cos\theta)=V_e r_p \cos\theta-V_e r_e \\ V_p r_p+V_e r_e=(V_p r_e+V_e r_p)\cos\theta\end{aligned}$$
反三角函数得到
$$\theta=arccos(\frac{V_p r_p+V_e r_e}{V_p r_e+V_e r_p})$$
冲日前后不大于$\theta$角的一段时间里，行星都处于逆行状态，因此逆行总时间为
$T=\frac{2\theta}{\omega_e-\omega_p}$

转载到请包括本文地址：https://kexue.fm/archives/958

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Oct. 02, 2010). 《关于行星留周期的几何讨论 》[Blog post]. Retrieved from https://kexue.fm/archives/958

@online{kexuefm-958,
        title={关于行星留周期的几何讨论},
        author={苏剑林},
        year={2010},
        month={Oct},
        url={\url{https://kexue.fm/archives/958}},
}