如何训练你的准确率？

最近Arxiv上的一篇论文《EXACT: How to Train Your Accuracy》引起了笔者的兴趣，顾名思义这是介绍如何直接以准确率为训练目标来训练模型的。正好笔者之前也对此有过一些分析，如《函数光滑化杂谈：不可导函数的可导逼近》、《再谈类别不平衡问题：调节权重与魔改Loss的对比联系》等， 所以带着之前的研究经验很快完成了论文的阅读，写下了这篇总结，并附上了最近关于这个主题的一些新思考。

失实的例子 #

论文开头指出，我们平时用的分类损失函数是交叉熵或者像SVM中的Hinge Loss，这两个损失均不能很好地拟合最终的评价指标准确率。为了说明这一点，论文举了一个很简单的例子：假设数据只有$\{(-0.25,-1),(0,-1),(0.25,,1)\}$三个点，$-1$和$1$分别代表负类和正类，待拟合模型是$f(x)=x-b$，$b$是参数，我们希望通过$\text{sign}(f(x))$来预测类别。如果用“sigmoid + 交叉熵”，那么损失函数就是$-\log \frac{1}{1+e^{-l \cdot f(x)}}$，$(x,l)$代表一对标签数据；如果用Hinge Loss，则是$\max(0, 1 - l\cdot f(x))$。

由于只是一个一维模型，我们可以直接网格搜索出它的最优解，可以发现如果用“sigmoid + 交叉熵”的话，损失函数的最小值在$b=0.7$取到，而如果是Hinge Loss，那么$b\in[0.75,1]$。然而，如果要通过$\text{sign}(f(x))$完全分类正确，那么$b\in(0, 0.25)$才行，因此这说明了交叉熵或Hinge Loss与最后评测指标准确率的不一致性。

看上去是一个很简明漂亮的例子，但笔者认为它是不符合事实的。其中，最大的问题是模型设置温度参数，即一般出现的模型是$f(x)=k(x-b)$而不是$f(x)=x-b$，刻意去掉温度参数来构造不符合事实的反例是没有说服力的，事实上补上可调的温度参数后，这两个损失都可以学到正确的答案。更不公平的是，后面作者在提出自己的方案EXACT时，是自带温度参数的，并且温度参数是关键一环，换句话说，在这个例子中，EXACT比其他两个损失好，纯粹是因为EXACT有温度参数。

新瓶装旧酒 #

然后我们来看论文所提出的方案——EXACT（EXpected ACcuracy opTimization）。从事后来看，EXACT很是莫名其妙，因为作者是直接不加任何解释地从重参数的角度重新定义了一个条件概率分布$p(y|x)$：
\begin{equation}p(y|x) = P\left(y = \mathop{\arg\max}_i \frac{\mu(x)}{\sigma(x)}+\varepsilon\right)\end{equation}
其中$\mu(x)$是一个向量网络，$\sigma(x)$是一个标量网络，$\varepsilon$跟$\mu(x)$维度相同，每个分量是独立同分布地从$\sim \mathcal{N}(0,1)$采样得到。关于用重参数来定义概率分布的做法，我们在上一篇文章《从重参数的角度看离散概率分布的构建》已经讨论过，这里不重复。

紧接着，有了这个新的$p(y|x)$，作者直接以
\begin{equation}-\mathbb{E}_{(x,y)\sim\mathcal{D}}[p(y|x)]\label{eq:soft-acc}\end{equation}
作为损失函数，全文的理论框架基本上到此结束。

由此，我们可以总结EXACT的莫名其妙之处了。在《从重参数的角度看离散概率分布的构建》我们知道，从重参数角度来看，Softmax对应的噪声分布是Gumbel分布，而EXACT换成了正态分布，那么好在哪？为什么会好？这些全无解释。

此外，式$\eqref{eq:soft-acc}$的相反数是准确率的光滑近似，这本已“广为人知”，但同时也有一个广为人知的结论是在Softmax情况下直接优化式$\eqref{eq:soft-acc}$的效果通常都是不如优化交叉熵的，现在只是换了一个“新瓶”（新概率分布的构建方法）装“旧酒”（同样的准确率光滑近似），真的就能有提升吗？

实验难复现 #

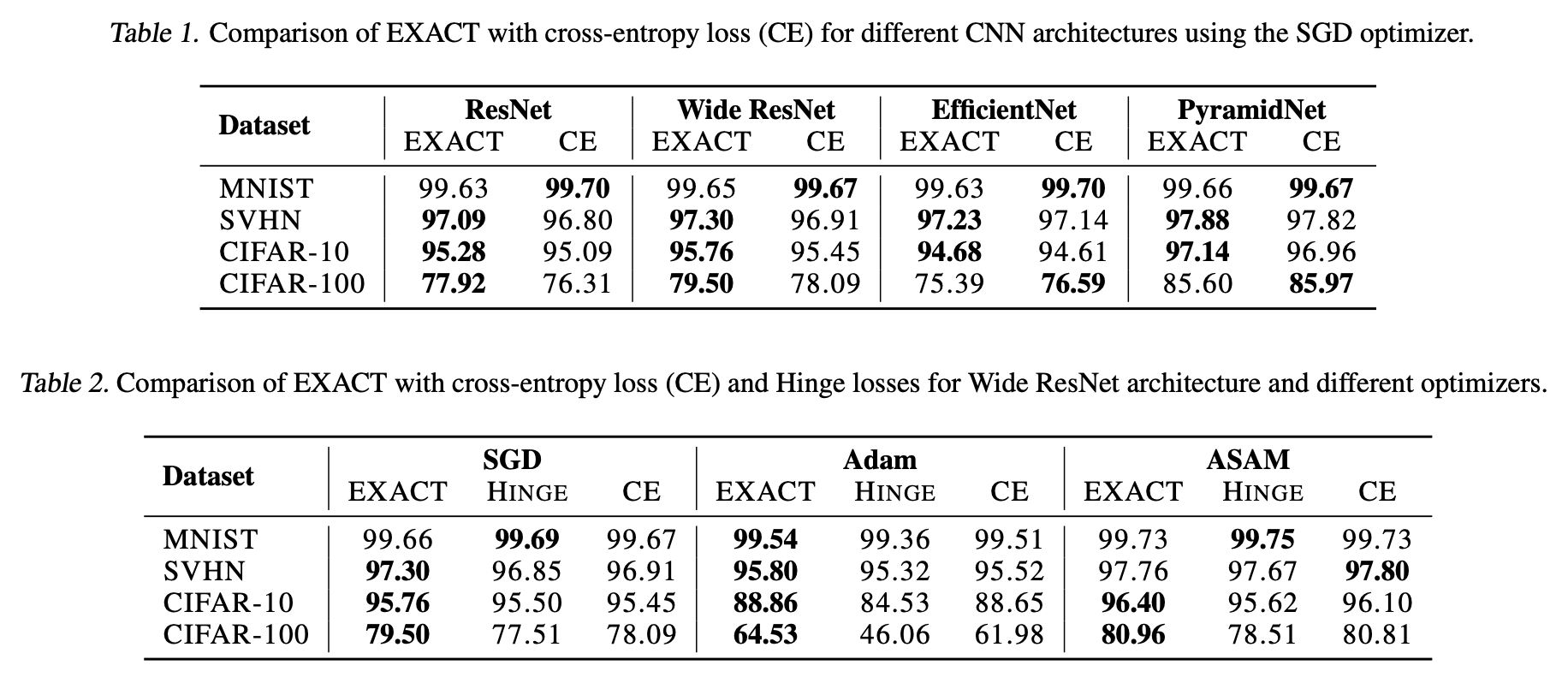
原论文给出了非常惊人的实验结果，显示EXACT几乎总是SOTA：

然而，笔者根据自己的理解尝试实现了EXACT，并在NLP任务上测试，结果显示EXACT完全不能达到“Softmax+交叉熵”的水平。此外，原论文还提到优化$-\log\mathbb{E}_{(x,y)\sim\mathcal{D}}[p(y|x)]$会比$\eqref{eq:soft-acc}$更好，但笔者的结果是该变体连$\eqref{eq:soft-acc}$都比不上。总的来说，笔者的测试结论与原论文是大相径庭的。

由于原论文还没有开源代码，因此笔者还不能对论文实验的可靠性做进一步的判断。但从笔者的理论理解和初步的实验结果来看，直接优化式$\eqref{eq:soft-acc}$是很不可能达到优化交叉熵的效果的，仅仅修改构建概率分布的方式，应该很难形成实质的提升。如果读者有新的实验结果，欢迎进一步交流分享。

一个新视角 #

从数值上来比较，式$\eqref{eq:soft-acc}$确实比交叉熵$\mathbb{E}_{(x,y)\sim\mathcal{D}}[-\log p(y|x)]$更贴合准确率。但为什么优化交叉熵往往能获得更好的的准确率？笔者原来也百思不得其解，在《再谈类别不平衡问题：调节权重与魔改Loss的对比联系》中，笔者设置将它视为“公理”来使用，实属无奈。

直到有一天，笔者突然意识到了一个关系：随着训练，多数$p(y|x)$会慢慢接近于1，于是可以用近似$\log x \approx x - 1$得到
\begin{equation}\mathbb{E}_{(x,y)\sim\mathcal{D}}[-\log p(y|x)]\approx \mathbb{E}_{(x,y)\sim\mathcal{D}}[1 - p(y|x)] = 1 - \mathbb{E}_{(x,y)\sim\mathcal{D}}[p(y|x)]\end{equation}
于是我们就能解释为什么优化交叉熵也能获得很好的准确率了，因为从上式我们可以发现，交叉熵优化到中后期跟式$\eqref{eq:soft-acc}$基本是等价的，也就是同样在优化准确率的光滑近似！

那交叉熵相比式$\eqref{eq:soft-acc}$的好处在哪呢？差别就在于当$p(y|x) \ll 1$时，$-\log p(y|x)$与$1 - p(y|x)$的差距。当$p(y|x) \ll 1$时，即目标类的概率很小，意味着分类可能很不准确，这时候$-\log p(y|x)$给出的是一个会趋于无穷大的结果，但$1 - p(y|x)$最多就只能给出$1$。这样一比较，我们就发现交叉熵的$-\log p(y|x)$对错误分类的样本的惩罚更大，因此它会更倾向于修正分类错误的样本，同时最终分类结果又跟直接优化准确率的光滑近似相近。

由此，我们可以得到一个优秀的损失函数的新视角：

首先寻找评测指标的一个光滑近似，最好能表达成每个样本的期望形式，然后将错误方向的误差逐渐拉到无穷大（保证模型能更关注错误样本），但同时在正确方向保证与原始形式是一阶近似。

最后的小结 #

本文主要讨论了如何优化准确率的问题，其中先简单介绍和评述了一下最近的论文《EXACT: How to Train Your Accuracy》，然后就“为什么优化交叉熵能获得更好的准确率结果”给出了自己的分析。

转载到请包括本文地址：https://kexue.fm/archives/9098

更详细的转载事宜请参考：《科学空间FAQ》