MoE环游记：5、均匀分布的反思

如果说Meta的LLAMA系列为Dense模型确立了标准架构，那么DeepSeek或许就是MoE标准架构的奠基者。当然，这并非指DeepSeek首创了MoE，也不是说它的MoE不可超越，而是指DeepSeek对MoE所提的一些改进，很可能都是效果增益比较显著的方向，从而逐渐成为MoE的标配。这其中，包括我们在《MoE环游记：3、换个思路来分配》介绍的Loss-Free负载均衡方案，还有本文将要介绍的Shared Expert、Fine-Grained Expert策略。

说到负载均衡，它无疑是MoE一个极为重要的目标，本系列的第2～4篇，可以说都在围绕着它展开。然而，已有读者逐渐意识到，这里边有个尚未回答的本质问题：抛开效率上的需求不谈，均匀分布就一定是效果最好的方向吗？本文就带着这个疑问，去理解Shared Expert、Fine-Grained Expert。

共享专家 #

让我们再次回顾MoE的基本形式
\begin{equation}\boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho}} \rho_i \boldsymbol{e}_i\end{equation}
除此之外，《MoE环游记：3、换个思路来分配》中的Loss-Free将$\mathop{\text{argtop}}_k \boldsymbol{\rho}$替换换成$\mathop{\text{argtop}}_k \boldsymbol{\rho}+\boldsymbol{b}$，还有在《MoE环游记：4、难处应当多投入》我们将它推广成$\mathop{\text{argwhere}} \boldsymbol{\rho}+\boldsymbol{b} > 0$，但这些变体跟Shared Expert技巧都是正交的，因此接下来只以最基本的形式为例。

Shared Expert将上式改为
\begin{equation}\boldsymbol{y} = \sum_{i=1}^s \boldsymbol{e}_i + \sum_{i\in \mathop{\text{argtop}}_{k-s} \boldsymbol{\rho}_{[s:]}} \rho_{i+s} \boldsymbol{e}_{i+s}\label{eq:share-1}\end{equation}
也就是说，将原本的$n$选$k$，改为$n-s$选$k-s$，另外$s$个Expert则必然会被选中，这部分就被称为“Shared Expert”，刚出来那会我们还戏称为“常任理事国”，剩下的$n-s$个Expert则被称为“Routed Expert”。其中，Shared Expert的数目$s$不会太大，通常是1或2，太大反而会让模型“冷落”了剩下的Routed Expert。

需要指出的是，开启Shared Expert前后，总Expert数都是$n$，激活的Expert都是$k$，所以Shared Expert原则上不增加模型参数量和推理成本。但即便如此，DeepSeekMoE和我们自己的一些实验显示，Shared Expert依然能一定程度上提升模型效果。

多种理解 #

我们可以从多个视角理解Shared Expert。比如残差视角，它指出Shared Expert技巧实际上是将原本学习每一个Expert，改为学习它跟Shared Expert的残差，这样能降低学习难度，还会有更好的梯度。用DeepSeek的话则是说：通过将共同知识压缩到这些Shared Expert中，减轻Routed Expert之间的冗余，提高参数效率并确保每个Routed Expert专注于独特方面。

如果将Routed Expert类比成中学各个学科的老师，那么Shared Expert就是类似“班主任”的存在。如果一个班只有科任老师，那么每个科任老师将不可避免地分摊一些管理工作，而设置班主任的角色，则将这些共同的管理工作集中在一个老师身上，让科任老师专注于学科教学，提高教学效率。

当然也可以从几何角度理解。Expert之间的不可避免的共性，几何意义是它们的向量夹角小于90度，这跟我们在《MoE环游记：1、从几何意义出发》提出MoE几何意义时所用的Expert向量“两两正交”假设矛盾。虽然说这个假设不成立时也能理解为近似解，但自然是越成立越好，而我们可以将Shared Expert理解成这些Routed Expert的均值，通过学习减去均值后的残差，使得正交假设更容易成立。

比例因子 #

我们将式$\eqref{eq:share-1}$一般地写成
\begin{equation}\boldsymbol{y} = \sum_{i=1}^s \boldsymbol{e}_i + \lambda\sum_{i\in \mathop{\text{argtop}}_{k-s} \boldsymbol{\rho}_{[s:]}} \rho_{i+s} \boldsymbol{e}_{i+s}\end{equation}

由于Routed Expert带有权重$\rho_{i+s}$而Shared Expert没有，以及Routed Expert的数目通常远大于Shared Expert数目（即$n - s \gg s$）等原因，它们的比例可能会失衡，因此为了让两者不至于被相互埋没，设置合理的$\lambda$尤为重要。对此，我们在《Muon is Scalable for LLM Training》提出，适当的$\lambda$应使得两者在初始化阶段模长接近一致。

具体来说，我们假设每个Expert在初始化阶段具有相同的模长（不失一般性，可以直接设为1），并且满足两两正交，然后假设Router的logits服从标准正态分布（即零均值、单位方差，当然如果觉得有必要，也可以考虑其他方差）。这样一来，$s$个Shared Expert的总模长就是$\sqrt{s}$，而Routed Expert的总模长是
\begin{equation}\lambda\sqrt{\sum_{i\in \mathop{\text{argtop}}_{k-s} \boldsymbol{\rho}_{[s:]}} \rho_{i+s}^2}\end{equation}
通过让它等于$\sqrt{s}$，就可以估计出$\lambda$。由于激活函数、是否重归一化等选择，不同MoE的Router差别可能比较大，所以我们也不设法求解析解，而是直接数值模拟：

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def softmax(x):
    return (p := np.exp(x)) / p.sum()

def scaling_factor(n, k, s, act='softmax', renorm=False):
    factors = []
    for _ in range(10000):
        logits = np.random.randn(n - s)
        p = np.sort(eval(act)(logits))[::-1][:k - s]
        if renorm:
            p /= p.sum()
        factors.append(s**0.5 / (p**2).sum()**0.5)
    return np.mean(factors)

scaling_factor(162, 8, 2, 'softmax', False)
scaling_factor(257, 9, 1, 'sigmoid', True)

非常巧的是，这个脚本的模拟结果跟DeepSeek-V2、DeepSeek-V3的设置都很吻合。其中，DeepSeek-V2有$n=162,k=8,s=2$，Softmax激活并且没有重归一化，上述脚本的模拟结果约等于16，而DeepSeek-V2的$\lambda$正好是16^[来源]；DeepSeek-V3则有$n=257,k=9,s=1$，Sigmoid激活且重归一化，脚本的结果大约是2.83，而DeepSeek-V3的$\lambda$则是2.5^[来源]。

非均匀性 #

回到文章开头的问题：均衡一定是效果最好的方向吗？看起来Shared Expert给了一个参考答案：未必。因为Shared Expert也可以理解为某些Expert一定会被激活，于是整体来看，这将导致一个非均匀的Expert分布：
\begin{equation}\boldsymbol{F} = \frac{1}{s+1}\bigg[\underbrace{1,\cdots,1\\}_{s个},\underbrace{\frac{1}{n-s},\cdots,\frac{1}{n-s}\\}_{n-s 个}\bigg]\end{equation}

实际上，非均匀分布在现实世界随处可见，所以均匀分布并非最优方向其实应该很容易接受。还是以前面的中学老师类比为例，同一个学校各个学科的老师数量其实是不均匀的，通常是语文、数学、英语最多，物理、化学、生物次之，体育、美术更少（还经常生病）。更多非均匀分布的例子，大家可以搜索一下Zipf定律。

总而言之，现实世界的非均匀性，必然会导致自然语言的非均匀性，从而导致均匀分布的非最优性。当然，从训练模型的角度看，均匀分布还是更容易并行和扩展，所以单独分离出一部分Shared Expert，剩下的Routed Expert仍然希望它均匀，是实现非均匀性的一种对双方都友好的折中选择，而不是直接让Routed Expert对齐一个非均匀分布。

刚才说的是训练，那推理呢？推理阶段可以事先预估Routed Expert的实际分布，并且不需要考虑反向传播，所以只要细致地进行优化，理论上可以做到效率不降的。但由于现在MoE的推理基建都是针对均匀分布设计的，并且单卡显存有限等实际限制，所以我们仍旧希望Routed Expert能均匀来实现更好的推理效率。

细颗粒度 #

除了Shared Expert外，DeepSeekMoE所提的另一个改进点是Fine-Grained Expert，它指出在总参数量和激活参数量都不变的情况下，Expert的颗粒度越细，效果往往越好。

比如，原本是$n$选$k$的Routed Expert，现在我们将每个Expert缩小一半，然后改成$2n$选$2k$，那么总参数量和激活的参数量都还是一样的，但后者表现往往更好。原论文的说法是这样丰富了Expert组合的多样性，即
\begin{equation}\binom{n}{k} \ll \binom{2n}{2k} \ll \binom{4n}{4k} \ll \cdots\end{equation}

当然，我们也可以有其他理解，比如说将Expert进一步分割成更小的单元，那么每个Expert可以专注于更狭窄的知识领域，从而实现更精细的知识分解，等等。但要注意，Fine-Grained Expert并非是无成本的，$n$越大，Expert之间的负载往往越不均衡，并且Expert之间的通信和协调成本也会增加，所以$n$也不能无限增加，有一个效果和效率都友好的舒适区间。

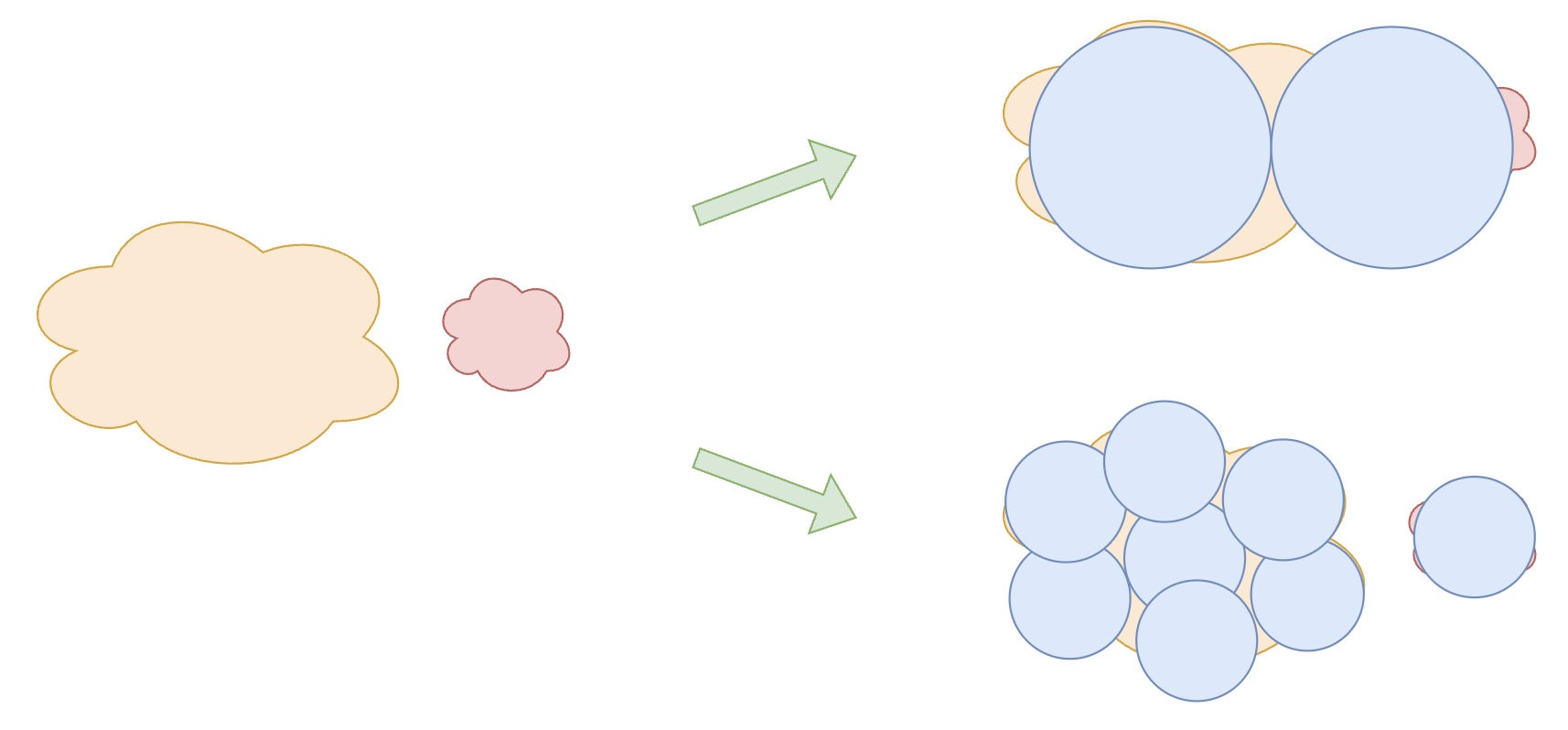
关于Fine-Grained Expert的有效性，笔者这里提出另外一种不大容易察觉的解释，它跟本文的主题有关：更多数量、更细颗粒度的Expert，可以更好地模拟现实世界的非均匀性。以下图为例，假设知识可以分为一大一小两类，每个Expert则是一个圆，如果我们用2个大圆去覆盖，那么存在一定的遗漏和浪费，而如果改用8个总面积相同的小圆，那么就可以覆盖得更为细致，因此效果更优。

文章小结 #

本文介绍了MoE的Shared Expert和Fine-Grained Expert策略，并指出它们某种程度上都体现了负载均衡的非最优性。

转载到请包括本文地址：https://kexue.fm/archives/10945

更详细的转载事宜请参考：《科学空间FAQ》