你跳绳的时候,想过绳子的形状曲线是怎样的吗?
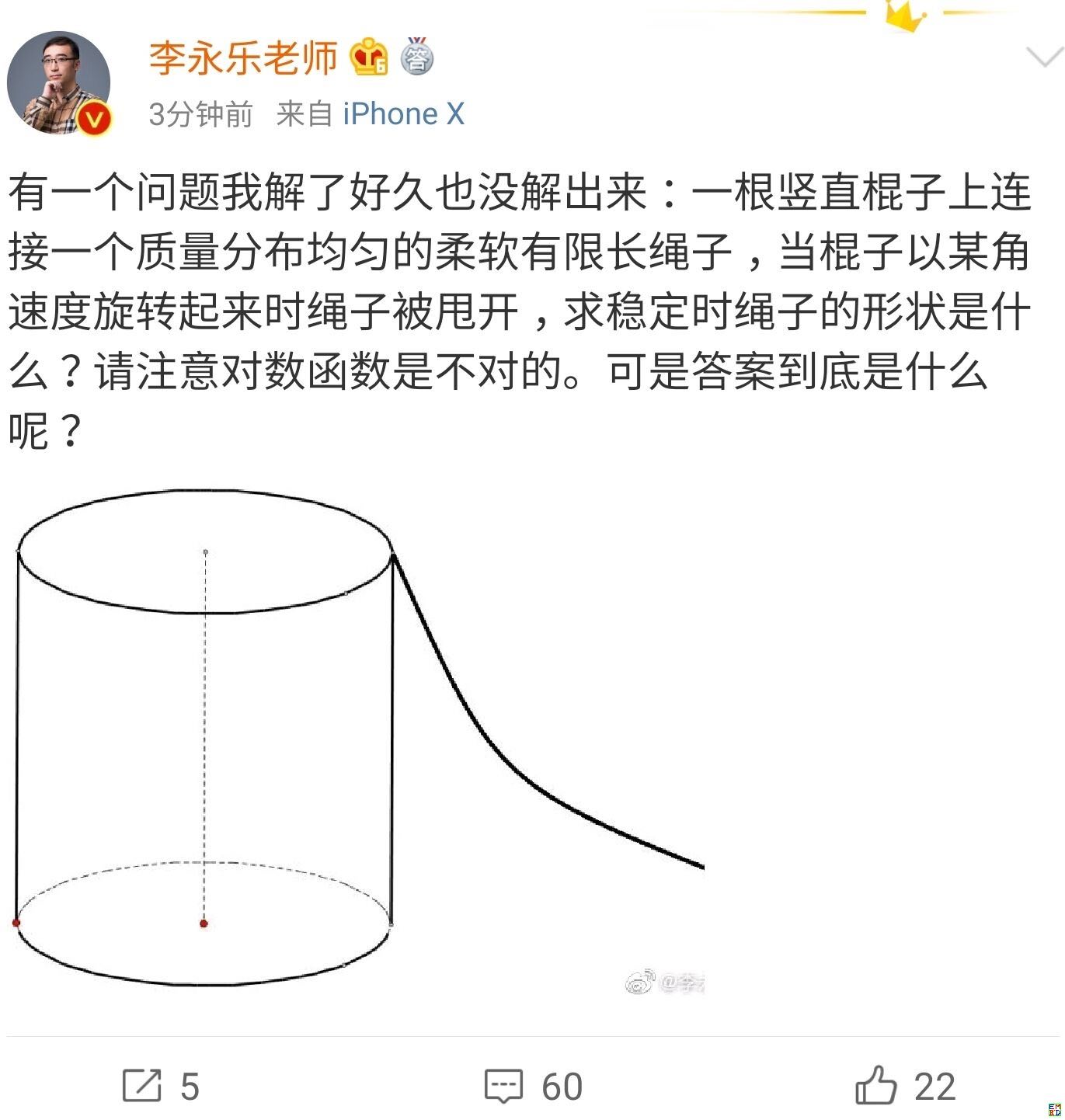
By 苏剑林 | 2019-07-06 | 65992位读者 |前几天,好几个数学/物理群都在转发李永乐老师发在他微博里的一道题:
想起好久没有做数学物理题了,所以我也思考了一下,也搜了一些资料,在此与大家分享一下。
相关内容 #
事实上,李永乐老师这样的提法,让人感觉这只是一个纯粹的物理练习题,但事实上这道题跟不少生活例子的曲线形状有关,比如,快速跳绳(绳子已经绷紧)的时候,绳子的形状是怎样的?
事实上,跳绳形状问题,跟李永乐老师提出的原始问题,本质上都是等价的,基本特点是:
1、有一条质地均匀的细绳子;
2、绳子在高速自旋,旋转的角速度$\omega$可以视为常数;
3、绳子还受到重力的作用;
4、求绳子达到(相对)静态平衡时的曲线形状。
当然,在生活中其实还会受到空气的阻力,使得平衡状态还不一定是平面曲线,最典型的例子无外乎市场上的驱蚊电风扇:
方程推导 #
在本文中,我们还是只关心在平面上形成平衡的情况,而在这一节里边,我们来推导相应的微分方程。笔者只是业余物理学爱好者,所以我不懂专业的受力分析,我只会基于变分法的最小作用量原理(参考本博客的《〈自然极值〉系列——8.极值分析》、《重提“旋转弹簧伸长”问题(变分解法)》、《关于“平衡态公理”的更正与思考》、《变分与理论力学略览》等,早期有不少关于物理和数学的文章。)。
最小作用量原理实则上要我们去变分动能减去势能的差,对于李永乐老师的原始问题,旋转运动是水平方向的,而重力是竖直方向的,假设线密度为1,那么动能和势能分别是:
\begin{equation}T = \int \frac{1}{2}\omega^2 x^2 \sqrt{dx^2+dy^2},\quad U = \int gy \sqrt{dx^2+dy^2}\end{equation}
所以实际上就是变分
\begin{equation}S = \int \left(\frac{1}{2}\omega^2 x^2 - gy\right)\sqrt{dx^2+dy^2} = \int \left(\frac{1}{2}\omega^2 x^2 - gy\right) ds\label{eq:t}\end{equation}
如果是跳绳问题,旋转和重力都是竖直方向的(只考虑绳子跳到最低处时的形状),所以变分的目标是
\begin{equation}S = \int \left(\frac{1}{2}\omega^2 y^2 - gy\right)ds\end{equation}
看上去跟$\eqref{eq:t}$差不多,但实际上它跟$\eqref{eq:t}$的难度有本质差别,因为只需要做一个变换$z = y - g/\omega^2$,那么它就等价于式$\eqref{eq:t}$在$g=0$的情形,而后面我们会看到这种特殊情况是可以求出解析解来的,而原始式$\eqref{eq:t}$则不行。
变分法用于绳子有两个边界点是确定的情况,但是对于李永乐老师的问题,似乎只有一个边界点是确定的,还可以用变分法吗?事实上也可以,我们可以设想另外一个边界点也确定了(但我们不知道是多少),这不改变它原有的形状和运动轨迹。
事不宜迟,我们正式进行变分。记
\begin{equation}\varphi(x, y) = \frac{1}{2}\omega^2 x^2 - gy\end{equation}
得到
\begin{equation}\begin{aligned}&\delta \int \varphi(x, y) ds \\
=& \int \left(\omega^2 x \delta x - g \delta y\right) ds + \varphi(x, y) \delta ds\\
=& \int \left(\omega^2 x \delta x - g \delta y\right) ds + \varphi(x, y) \frac{dx \delta dx + dy \delta dy}{ds}\\
=& \int \left(\omega^2 x \delta x - g \delta y\right) ds + \varphi(x, y) \left(\frac{dx}{ds}d\delta x + \frac{dy}{ds}d\delta y\right)\\
=& \int \left(\omega^2 x \delta x - g \delta y\right) ds - d\left(\varphi(x, y) \frac{dx}{ds}\right)\delta x - d\left(\varphi(x, y) \frac{dy}{ds}\right)\delta y\end{aligned}\end{equation}
其中最后一个等号用到了分部积分法,并且利用了边界条件为0的约定,这都是变分法的常规操作。接着我们整理得到:
\begin{equation}\begin{aligned}&\delta \int \varphi(x, y) ds \\
=& \int \left[\left(\omega^2 x - \frac{d}{ds}\left(\varphi(x, y) \frac{dx}{ds}\right)\right)\delta x + \left(-g - \frac{d}{ds}\left(\varphi(x, y) \frac{dy}{ds}\right)\right)\delta y\right]ds\end{aligned}\end{equation}
让$\delta x, \delta y$两项恒为0,得到微分方程组
\begin{equation}\left\{\begin{aligned}&\frac{d}{ds}\left(\varphi(x, y) \frac{dx}{ds}\right)=\omega^2 x\\
&\frac{d}{ds}\left(\varphi(x, y) \frac{dy}{ds}\right) = -g
\end{aligned}\right.\end{equation}
同时还有条件
\begin{equation}\left(\frac{dx}{ds}\right)^2 + \left(\frac{dy}{ds}\right)^2 = 1\label{eq:ode1}\end{equation}
由第二个微分方程直接得到
\begin{equation}\varphi(x, y) \frac{dy}{ds} = -gs + C_1\label{eq:ode2}\end{equation}
就用$\eqref{eq:ode1}$和$\eqref{eq:ode2}$,再加上边界条件,理论上就可以将曲线的形状解出来。
两个特例 #
目前看来,解析地求解$\eqref{eq:ode1}$和$\eqref{eq:ode2}$是不可能的,所以我们可以分析一些特例,最简单的两个特例无外乎$\omega=0$或者$g=0$。
ω = 0 #
对于$\omega=0$,如果是李永乐老师的问题,那答案是平凡的:就是一条竖直向下的直线而已。但事实上我们可以在它的基础上增加额外的边界条件,使得结果非平凡——实际上就是一条“悬链线”。悬链线我们以前也求解过,参考《〈自然极值〉系列——7.悬链线问题》,这里沿着$\eqref{eq:ode1}$和$\eqref{eq:ode2}$重新推导一次。当$\omega=0$时,$\eqref{eq:ode2}$变为
\begin{equation}-gy\frac{dy}{ds} = -gs + C_1\end{equation}
或者等价地
\begin{equation}\frac{1}{2}\frac{d\left(y^2\right)}{ds} = s + C_1\end{equation}
(记原来的$-C_1/g$为新的$C_1$),那么解得:
\begin{equation}y^2 = s^2 + 2C_1 s + C_2\end{equation}
不失一般性我们设$C_1=0$,那么(选择适当的坐标系可以使得$C_2$非负,所以可以记为$C_2=a^2$)
\begin{equation}s = \sqrt{y^2 - a^2}\quad \Rightarrow\quad ds = \frac{y dy}{\sqrt{y^2 - a^2}}\end{equation}
所以
\begin{equation}\frac{\sqrt{dx^2 + dy^2}}{dy} = \frac{y}{\sqrt{y^2 - a^2}}\quad \Rightarrow\quad
\frac{dx}{dy}=\frac{1}{\sqrt{y^2 - a^2}}\end{equation}
最后解得
\begin{equation}x = \text{arccosh}\left(\frac{y}{a}\right) + b\quad \Rightarrow\quad y = a\cosh \,(x - b)\end{equation}
这就是悬链线方程。
g = 0 #
前面已经讨论过,当$g=0$时,事实上就对应着跳绳的时候绳子的形状,它也叫做Rope skipping curve或者Troposkien curve,,此时$\eqref{eq:ode2}$变为
\begin{equation}\frac{1}{2}\omega^2 x^2 \frac{dy}{ds} = C_1\quad \Rightarrow\quad \frac{\sqrt{dx^2 + dy^2}}{dy} = \beta x^2\end{equation}
也就是
\begin{equation}y=\int \frac{1}{\sqrt{\beta^2 x^4 - 1}}dx\end{equation}
这就是椭圆积分的事情了。
一般情形 #
当$\omega,g$都不等于0的时候,英文的搜索的关键字大概是Shape of rotating rope / spinning lasso,在stackexchange上也有人讨论过,如果能访问Google的朋友,还可以看看这里。
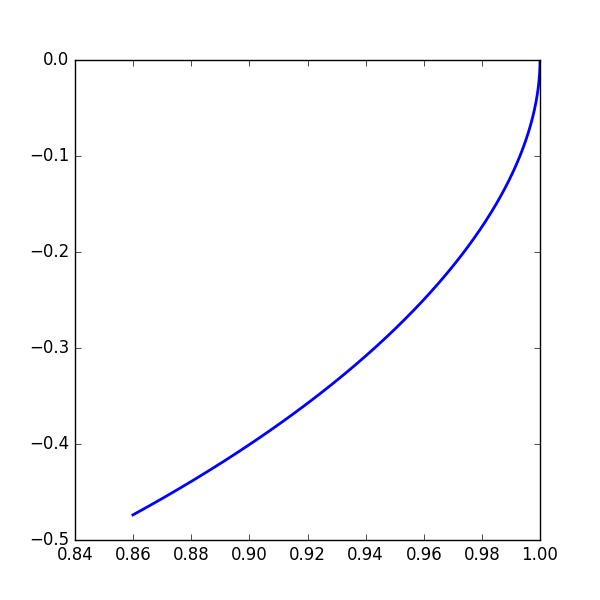
解析求解不行,不妨碍数值求解,比如:
参考代码(Python)为
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
omega = 2
g = 3
T = 0.5
h = 0.0001
C1 = 0
def F(t, x):
x, y = x
G = (C1 - g * t) / (1 / 2. * omega**2 * x**2 - g * y)
return [G, - np.sqrt(1 - G**2)]
x0, y0 = 1, 0.
ts = np.arange(0, T, h)
xs = solve_ivp(F, (0, T), [x0, y0], method='RK23', t_eval=ts)
x, y = xs.y
ts = xs.t
plt.clf()
plt.figure(figsize=(6, 6))
plt.plot(x, y, linewidth=2)
# plt.xlim(0.9, 1.15)
# plt.ylim(-0.25, 0)
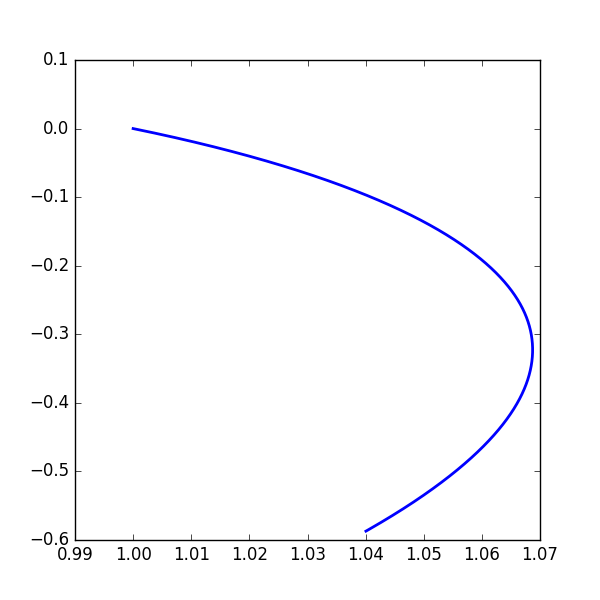
plt.savefig('test.png')前面也说过,该问题最一般的提法应该是两个端点都固定的,所以调整不同的C1,我们可能得到这样的曲线(对应C1=1,即所谓的“非平凡解”):
更多相关讨论可以参考知乎:https://www.zhihu.com/question/332446554/answer/746737923
文末感想 #
蹭一蹭李永乐老师这道题目的热度,顺便把以前的物理知识复习一下,就做了做这道题,当然最终也没能彻底解决,一般情况还是回归到了数值求解。不过在这个过程中搜索资料的收获,还是蛮丰富的。
曾经我有一个梦想,是当一个数学家/物理学家/天文学家,结果到了机器学习领域去打杂~~
转载到请包括本文地址:https://kexue.fm/archives/6784
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 06, 2019). 《你跳绳的时候,想过绳子的形状曲线是怎样的吗? 》[Blog post]. Retrieved from https://kexue.fm/archives/6784
@online{kexuefm-6784,
title={你跳绳的时候,想过绳子的形状曲线是怎样的吗?},
author={苏剑林},
year={2019},
month={Jul},
url={\url{https://kexue.fm/archives/6784}},
}












July 13th, 2019
博主,其实三次函数在一些情况下是个比较好的近似解
July 19th, 2022
(1)和(2)的dx dy漏了平方?
对对,已经修正。
June 2nd, 2023
公式1左式子少了x^2
谢谢,已修正