强大的NVAE:以后再也不能说VAE生成的图像模糊了
By 苏剑林 | 2020-07-10 | 164005位读者 |昨天早上,笔者在日常刷arixv的时候,然后被一篇新出来的论文震惊了!论文名字叫做《NVAE: A Deep Hierarchical Variational Autoencoder》,顾名思义是做VAE的改进工作的,提出了一个叫NVAE的新模型。说实话,笔者点进去的时候是不抱什么希望的,因为笔者也算是对VAE有一定的了解,觉得VAE在生成模型方面的能力终究是有限的。结果,论文打开了,呈现出来的画风是这样的:
然后笔者的第一感觉是这样的:
W!T!F! 这真的是VAE生成的效果?这还是我认识的VAE么?看来我对VAE的认识还是太肤浅了啊,以后再也不能说VAE生成的图像模糊了...
不过再看了看作者机构,原来是NVIDIA,这也大概能接受了。最近几年可能大家都留意到NVIDIA通常都在年底发布个生成模型的突破,2017年底是PGGAN,2018年底是StyleGAN,2019年底是StyleGAN2,今年貌似早了些,而且动作也多了些,因为上个月才发了个叫ADA的方法,将Cifar-10的生成效果提到了一个新高度,现在又来了个NVAE。
那这个NVAE究竟有什么特别的地方,可以实现VAE生成效果的突飞猛进呢?
VAE回顾 #
可能读者认真观察后会说:
好像还是有点假呀,那脸部也太光滑了,好像磨过皮一样,还比不上StyleGAN呀~
是的,这样评价并没有错,生成痕迹还是挺明显的。但如果你没感觉到震惊,那估计是因为你没看过之前的VAE生成效果,一般的VAE生成画风是这样的:
所以,你还觉得这不是一个突破吗?
那么,是什么限制了(以前的)VAE的表达能力呢?这一次的突破又是因为改进了哪里呢?让我们继续看下去。
基本介绍 #
VAE,即变分自编码器(Variational Auto-Encoder),本空间已经有不少文章介绍过了,在右侧搜索栏搜索“变分自编码器”就能搜到很多相关博文。这里做个简单的回顾和分析。
在笔者对VAE的推导里边,我们是先有一批样本,这批样本代表着一个真实的(但不知道形式的)分布$\tilde{p}(x)$,然后我们构建一个带参数的后验分布$p(z|x)$,两者就组成一个联合分布$p(x,z)=\tilde{p}(x)p(z|x)$。接着,我们再定义一个先验分布$q(z)$,已经定义一个生成分布$q(x|z)$,这样构成另一个联合分布$q(x,z)=q(z)q(x|z)$。最后,我们的目的就是让$p(x,z),q(x,z)$相互接近起来,所以我们去优化两者之间的KL散度:
\begin{equation}\begin{aligned}
KL\big(p(x,z)\big\Vert q(x,z)\big)=&\iint p(x,z)\log \frac{p(x,z)}{q(x,z)} dzdx\\
=&\mathbb{E}_{x\sim \tilde{p}(x)} \Big[\mathbb{E}_{z\sim p(z|x)}\big[-\log q(x|z)\big]+KL\big(p(z|x)\big\Vert q(z)\big)\Big] + \text{常数}
\end{aligned}\end{equation}
这就是VAE的优化目标。
困难分析 #
对$p(z|x),q(z),q(x|z)$的要求是:1、能写出解析表达式;2、方便采样。然而连续型分布的世界里这样的分布并不多,最常用的也就是高斯分布了,而这其中又以“各分量独立的高斯分布”最为简单,所以在一般的VAE里边,$p(z|x),q(z),q(x|z)$都被设为各分量独立的高斯分布:$p(z|x)=\mathcal{N}(z;\mu_1(x),\sigma_1^2(x))$、$q(z)=\mathcal{N}(z;0,1)$以及$q(x|z)=\mathcal{N}(x;\mu_2(z),\sigma_2^2(z))$。
问题是,“各分量独立的高斯分布”不能拟合任意复杂的分布,当我们选定$p(z|x)$的形式后,有可能不管我们怎么调它的参数,$\int \tilde{p}(x)p(z|x)dx$和$\frac{\tilde{p}(x)p(z|x)}{\int \tilde{p}(x)p(z|x)dx}$都不能成为高斯分布,这就意味着$KL\big(p(x,z)\big\Vert q(x,z)\big)$从理论上来说就不可能为0,所以让$p(x,z),q(x,z)$相互逼近的话,只能得到一个大致、平均的结果,这也就是常规VAE生成的图像偏模糊的原因。
相关改进 #
改进VAE的一个经典方向是将VAE与GAN结合起来,比如CVAE-GAN、AGE等,目前这个方向最先进结果大概是IntroVAE。从理论上来讲,这类工作相当于隐式地放弃了$q(x|z)$是高斯分布的假设,换成了更一般的分布,所以能提升生成效果。不过笔者觉得,将GAN引入到VAE中有点像“与虎谋皮”,借助GAN提升了性能,但也引入了GAN的缺点(训练不稳定等),而且提升了性能的VAE生成效果依然不如纯GAN的。另外一个方向是将VAE跟flow模型结合起来,比如IAF-VAE以及笔者之前做的f-VAE,这类工作则是通过flow模型来增强$p(z|x)$或$q(x|z)$的表达能力。
还有一个方向是引入离散的隐变量,典型代表就是VQ-VAE,其介绍可以看笔者的《VQ-VAE的简明介绍:量子化自编码器》。VQ-VAE通过特定的编码技巧将图片编码为一个离散型序列,然后PixelCNN来建模对应的先验分布$q(z)$。前面说到,当$z$为连续变量时,可选的$p(z|x),q(z)$都不多,从而逼近精度有限;但如果$z$是离散序列的话,$p(z|x),q(z)$对应离散型分布,而利用自回归模型(NLP中称为语言模型,CV中称为PixelRNN/PixelCNN等)我们可以逼近任意的离散型分布,因此整体可以逼近得更精确,从而改善生成效果。其后的升级版VQ-VAE-2进一步肯定了这条路的有效性,但整体而言,VQ-VAE的流程已经与常规VAE有很大出入了,有时候不大好将它视为VAE的变体。
NVAE梳理 #
铺垫了这么久,总算能谈到NVAE了。NVAE全称是Nouveau VAE(难道不是Nvidia VAE?),它包含了很多当前CV领域的新成果,其中包括多尺度架构、可分离卷积、swish激活函数、flow模型等,可谓融百家之所长,遂成当前最强VAE~
(提醒,本文的记号与原论文、常见的VAE介绍均有所不同,但与本博客其他相关文章是一致的,望读者不要死记符号,而是根据符号的实际含义来理解文章。)
自回归分布 #
前面我们已经分析了,VAE的困难源于$p(z|x),q(z),q(x|z)$不够强,所以改进的思路都是要增强它们。首先,NVAE不改变$q(x|z)$,这主要是为了保持生成的并行性,然后是通过自回归模型增强了先验分布$q(z)$和后验分布$p(z|x)$。具体来说,它将隐变量分组为$z=\{z_1,z_2,\dots,z_L\}$,其中各个$z_l$还是一个向量(而非一个数),然后让
\begin{equation}q(z)=\prod_{l=1}^L q(z_l|z_{< l}),\quad p(z|x)=\prod_{l=1}^L p(z_l|z_{< l},x)\label{eq:arpq}\end{equation}
而各个组的$q(z_l|z_{< l}),p(z_l|z_{< l},x)$依旧建立为高斯分布,所以总的来说$q(z),p(z|x)$就被建立为自回归高斯模型。这时候的后验分布的KL散度项变为
\begin{equation}KL\big(p(z|x)\big\Vert q(z)\big)=KL\big(p(z_1|x)\big\Vert q(z_1)\big)+\sum_{l=2}^L \mathbb{E}_{p(z_{< l}|x)}\Big[KL\big(p(z_l|z_{< l}, x)\big\Vert q(z_l|z_{< l})\big)\Big]\end{equation}
当然,这个做法只是很朴素的推广,并非NVAE的首创,它可以追溯到2015年的DRAW、HVM等模型。NVAE的贡献是给式$\eqref{eq:arpq}$提出了一种“相对式”的设计:
\begin{equation}\begin{aligned}&q(z_l|z_{< l})=\mathcal{N}\left(z_l;\mu(z_{< l}),\sigma^2(z_{< l})\right)\\
&p(z_l|z_{< l},x)=\mathcal{N}\left(z_l;\mu(z_{< l})+\Delta\mu(z_{< l},x),\sigma^2(z_{< l})\otimes \Delta\sigma^2(z_{< l}, x)\right)
\end{aligned}\end{equation}
也就是说,没有直接去后验分布$p(z_l|z_{< l},x)$的均值方差,而是去建模的是它与先验分布的均值方差的相对值,这时候我们有(简单起见省去了自变量记号,但不难对应理解)
\begin{equation}KL\big(p(z_l|z_{< l}, x)\big\Vert q(z_l|z_{< l})\big)=\frac{1}{2} \sum_{i=1}^{|z_l|} \left(\frac{\Delta\mu_{(i)}^2}{\sigma_{(i)}^2} + \Delta\sigma_{(i)}^2 - \log \Delta\sigma_{(i)}^2 - 1\right)\end{equation}
原论文指出这样做能使得训练更加稳定。
多尺度设计 #
现在隐变量分成了$L$组$z=\{z_1,z_2,\dots,z_L\}$,那么问题就来了:1、编码器如何一一生成$z_1,z_2,\dots,z_L$?2、解码器如何一一利用$z_1,z_2,\dots,z_L$?也就是说,编码器和解码器如何设计?
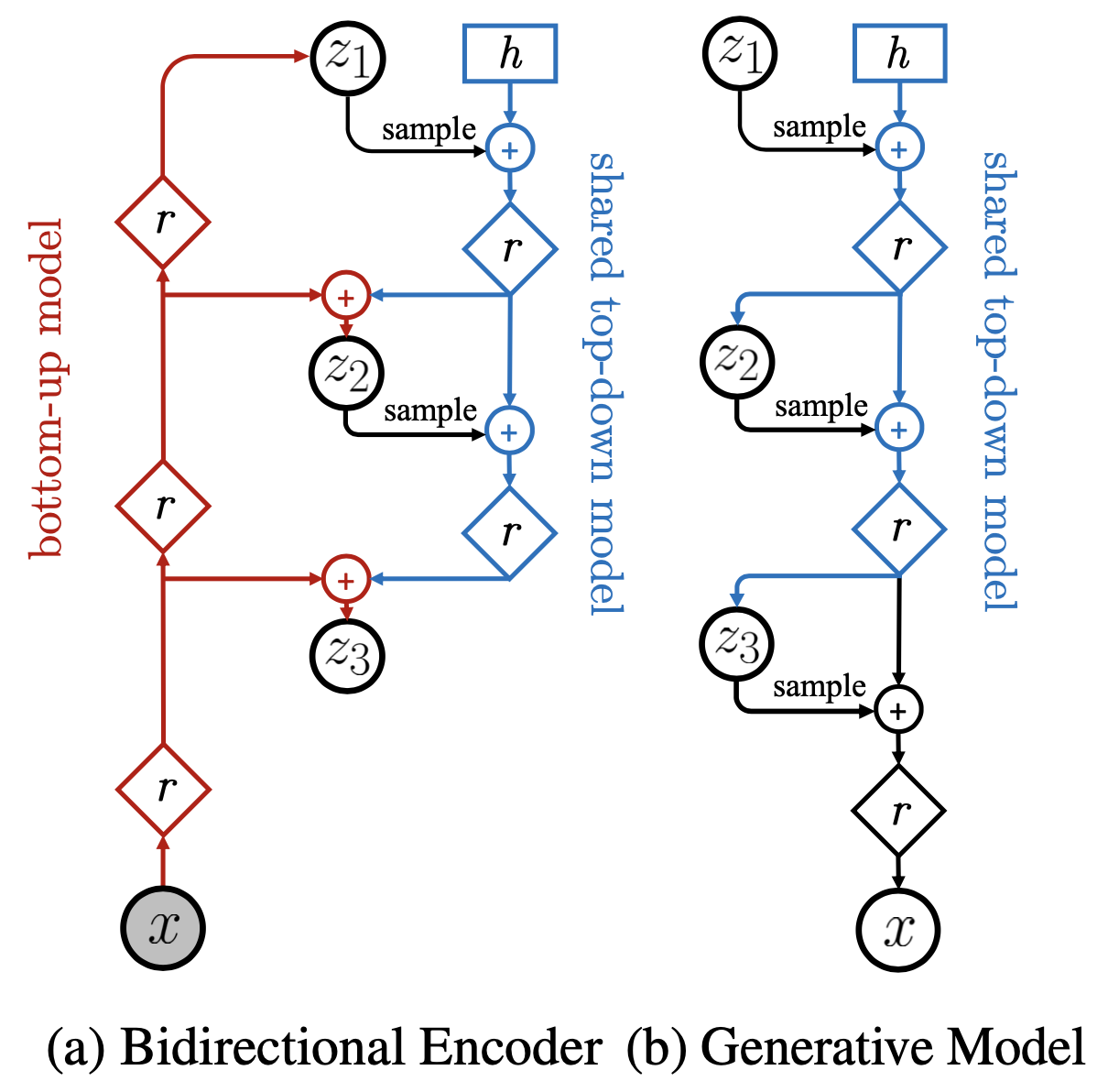
NVAE巧妙地设计了多尺度的编码器和解码器,如上图所示。首先,编码器经过层层编码,得到最顶层的编码向量$z_1$,然后再慢慢地从顶层往下走,逐步得到底层的特征$z_2,\dots,z_L$;至于解码器,自然也是一个自上往下地利用$z_1,z_2,\dots,z_L$的过程,而这部分刚好也是与编码器生成$z_1,z_2,\dots,z_L$的过程有共同之处,所有NVAE直接让对应的部分参数共享,这样既省了参数量,也能通过两者间的相互约束提高泛化性能。
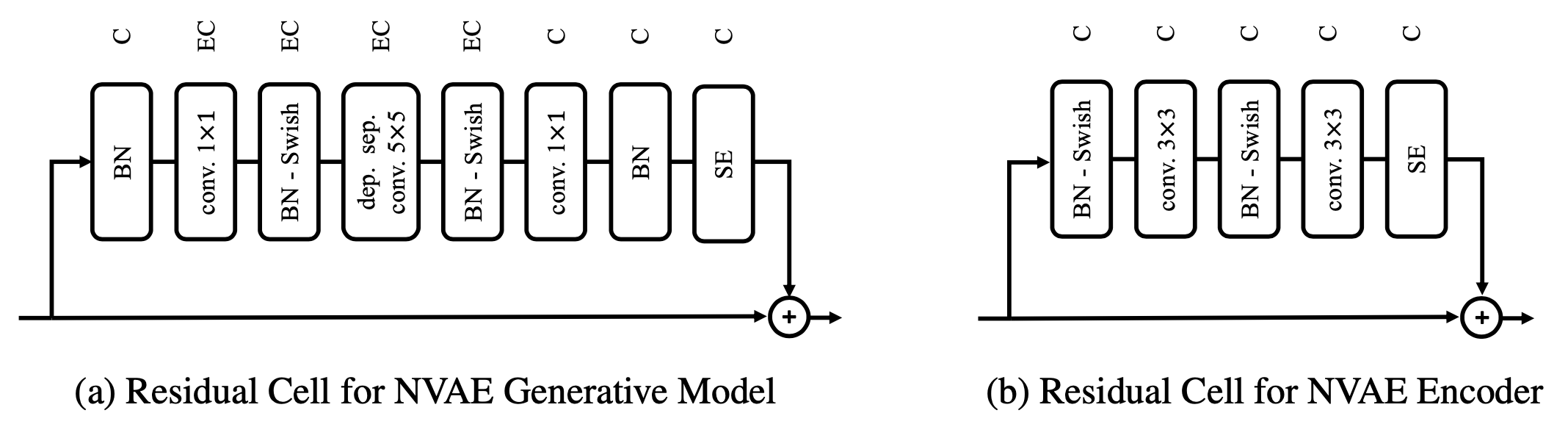
这种多尺度设计在当前最先进的生成模型都有体现,比如StyleGAN、BigGAN、VQ-VAE-2等,这说明多尺度设计的有效性已经得到比较充分的验证。此外,为了保证性能,NVAE还对残差模块的设计做了仔细的筛选,最后才确定了如下的残差模块,这炼丹不可谓不充分极致了:
其他提升技巧 #
除了以上两点比较明显的特征外,其实NVAE还包含了很多对性能有一定提升的技巧,这里简单列举一些。
BN层的改进。当前很多生成模型已经弃用BN(Batch Normalization)了,多数会改用IN(Instance Normalization)或WN(Weight Normalization),因为发现用BN会损失性能。NVAE通过实验发现,其实BN对训练还是有帮助的,但对预测有害,原因是预测阶段所使用的滑动平均得来的均值方差不够好,所以NVAE在模型训练完后,通过多次采样同样batch_size的样本来重新估算均值方差,从而保证了BN的预测性能。此外,为了保证训练的稳定性,NVAE还给BN的$\gamma$的模长加了个正则项。
谱正则化的应用。我们知道,任意两个分布的KL散度是无上界的,所以VAE里边的KL散度项也是无上界的,而优化这种无上界的目标是很“危险”的,说不准啥时候就发散了。所以同样是为了稳定训练,NVAE给每一个卷积层都加了谱正则化,其概念可以参考笔者之前的《深度学习中的Lipschitz约束:泛化与生成模型》。加谱归一化可以使得模型的Lipschitz常数变小,从而使得整个模型的Landscape更为光滑,更利于模型稳定训练。
flow模型增强分布。通过自回归模型,NVAE增强了模型对分布的拟合能力。不过这个自回归只是对组间进行的,对于组内的单个分布$p(z_l|z_{< l}, x)$和$q(z_l|z_{< l})$,依然假设为各分量独立的高斯分布,这说明拟合能力依然有提升空间。更彻底的方案是,对于组内的每个分量也假设为自回归分布,但是这样一来在采样的时候就巨慢无比了(所有的分量串联递归采样)。NVAE提供了一个备选的方案,通过将组内分布建立为flow模型来增强模型的表达能力,同时保持组内采样的并行性。实验结果显示这是有提升的,但笔者认为引入flow模型会大大增加模型的复杂度,而且提升也不是特别明显,感觉能不用就不用为好。
节省显存的技巧。尽管NVIDIA应该不缺显卡,但NVAE在实现上还是为省显存下了点功夫。一方面,它采用了混合精度训练,还顺带在论文推了一波自家的APEX库。另一方面,它在BN那里启用了gradient check-point(也就是重计算)技术,据说能在几乎不影响速度的情况下节省18%的显存。总之,比你多卡的团队也比你更会省显存~
更多效果图 #
到这里,NVAE的技术要点基本上已经介绍完毕了。如果大家还觉得意犹未尽的话,那就多放几张效果图吧,让大家更深刻地体会NVAE的惊艳之处。
个人收获 #
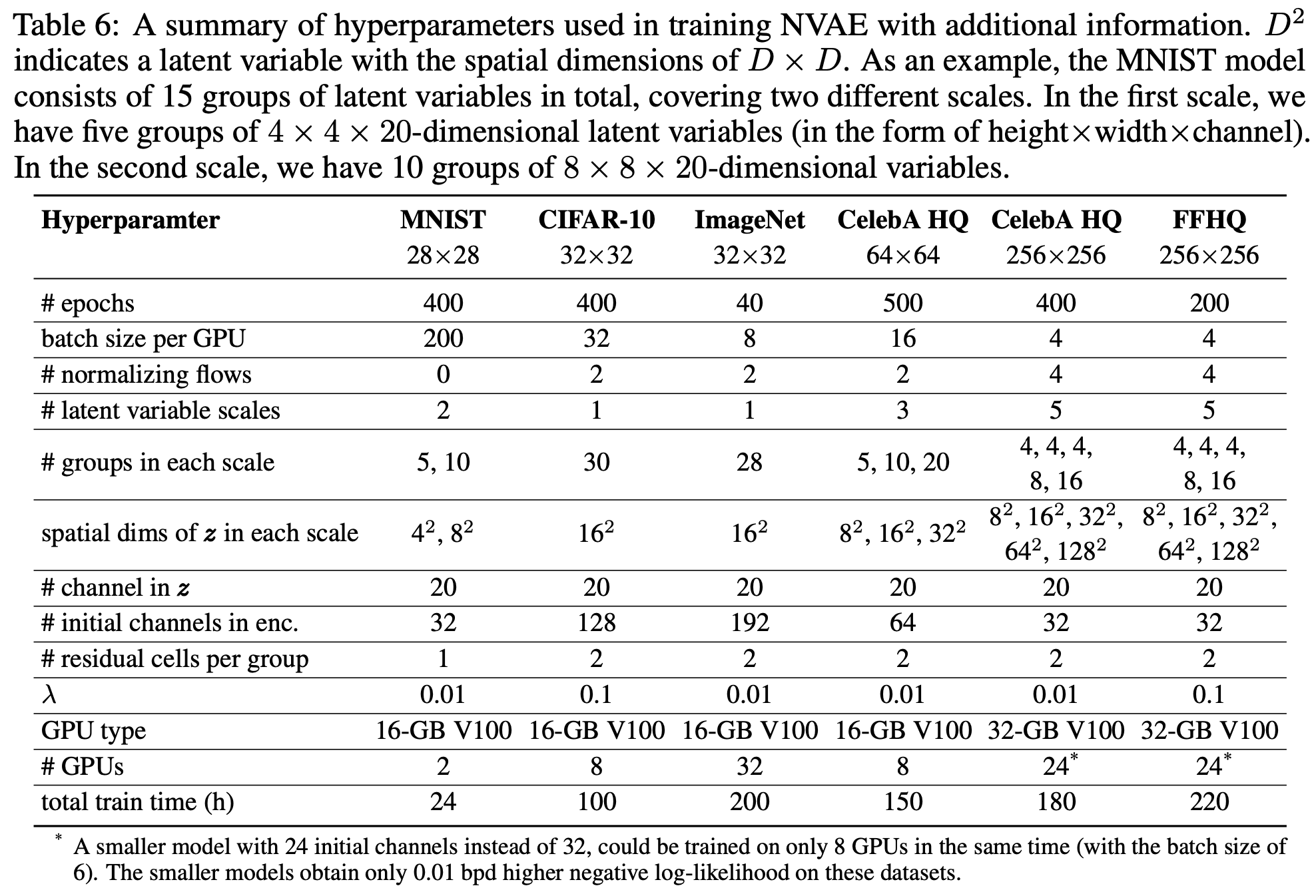
从下述训练表格来看,我们可以看到训练成本还是蛮大的,比同样分辨率的StyleGAN都要大,并且纵观整篇论文,可以发现有很多大大小小的训练trick(估计还有不少是没写在论文里边的,当然,其实在StyleGAN和BigGAN里边也包含了很多类似的trick,所以这不算是NVAE的缺点),因此对于个人来说,估计是不容易复现NVAE的。那么,对于仅仅是有点爱好生成模型的平民百姓(比如笔者)来说,从NVAE中可以收获到什么呢?
对于笔者来说,NVAE带来的思想冲击主要有两个。
第一,就是自回归的高斯模型可以很有力地拟合复杂的连续型分布。以前笔者以为只有离散分布才能用自回归模型来拟合,所以笔者觉得在编码时,也需要保持编码空间的离散型,也就是VQ-VAE那一条路。而NVAE证明了,哪怕隐变量是连续型的,自回归高斯分布也能很好地拟合,所以不一定要走VQ-VAE的离散化道路了,毕竟连续的隐变量比离散的隐变量更容易训练。
第二,VAE的隐变量可以不止一个,可以有多个的、分层次的。我们再次留意上表,比如FFHQ那一列,关于隐变量$z$的几个数据,他一共有$4+4+4+8+16=36$组,每组隐变量大小还不一样,分别是$\left\{8^2,16^2,32^2,64^2,128^2\right\}\times 20$,如此算来,要生成一个$256\times 256$的FFHQ图像,需要一个总大小有
\begin{equation}\left(4\times 8^2 + 4\times 16^2 + 4\times 32^2 + 8\times 64^2 + 16\times 128^2 \right)\times 20=6005760\end{equation}
维的随机向量,也就是说,采样一个600万维的向量,生成一个$256\times 256\times 3 = 196608$(不到20万)维的向量。这跟传统的VAE很不一样,传统的VAE一般只是将图片编码为单个(几百维)的向量,而这里的编码向量则多得多,有点全卷积自编码器的味道了,所以清晰度提升也是情理之中。
Nouveau是啥? #
最后,笔者饶有性质地搜索了一下Nouveau的含义,以下是来自维基百科的解释:
nouveau (/nuːˈvoʊ/) 是一个自由及开放源代码显卡驱动程序,是为Nvidia的显卡所编写,也可用于属于系统芯片的NVIDIA Tegra系列,此驱动程序是由一群独立的软件工程师所编写,Nvidia的员工也提供了少许帮助。 该项目的目标为利用逆向工程Nvidia的专有Linux驱动程序来创造一个开放源代码的驱动程序。由让freedesktop.org托管的X.Org基金会所管理,并以Mesa 3D的一部分进行散布,该项目最初是基于只有2D绘图能力的“nv”自由与开放源代码驱动程序所开发的,但红帽公司的开发者Matthew Garrett及其他人表示原先的代码被混淆处理过了。nouveau以MIT许可证许可。 项目的名称是从法文的“nouveau”而来,意思是“新的”。这个名字是由原作者的的IRC客户端的自动取代功能所建议的,当他键入“nv”时就被建议改为“nouveau”。
这是不是说,其实 Nouveau VAE 跟 Nvidia VAE 算是同义词了呢?原来咱们开始的理解也并没有错呀~
文章小结 #
本文介绍了NVIDIA新发表的一个称之为NVAE的升级版VAE,它将VAE的生成效果推向了一个新的高度。从文章可以看出,NVAE通过自回归形式的隐变量分布提升了理论上限,设计了巧妙的编码-解码结构,并且几乎融合了当前所有生成模型的最先进技术,打造成了当前最强的VAE~
转载到请包括本文地址:https://kexue.fm/archives/7574
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 10, 2020). 《强大的NVAE:以后再也不能说VAE生成的图像模糊了 》[Blog post]. Retrieved from https://kexue.fm/archives/7574
@online{kexuefm-7574,
title={强大的NVAE:以后再也不能说VAE生成的图像模糊了},
author={苏剑林},
year={2020},
month={Jul},
url={\url{https://kexue.fm/archives/7574}},
}















March 9th, 2022
苏神,多尺度框架具体是什么意思
在生成模型中,大致是指隐变量$z$同时加入到生成器的不同层中,而不单单像传统的生成器一样只加入到输入层中。
好的,谢谢
March 11th, 2022
分组里面隐变量的数量对先验分布、后验分布的表达能力有影响吗?每个分组中依然是独立高斯分布,如果减少每个分组中隐变量的数量,甚至每个分组只包含一个隐变量,是不是意味着表达能力会变强
每个分组只包含一个隐变量,理论上效果肯定是最强的,但采样速度也是最慢的。
April 14th, 2022
苏老师,请问一下(4)式中比如取$l=3$,那么$\Delta \mu(z_{ < 3},x)$依赖于$z_{1}$和$z_{2}$,但是下面图中的编码器里面$z_{3}$的红线输入部分似乎只依赖于$x$,不能看出其直接依赖于$z_{1}$和$z_{2}$,因为我理解的是编码器红线部分是产生$\Delta \mu(z_{ < l},x)$,而蓝线部分产生的是$\mu(z_{ < l})$,不知道是不是理解的问题,还请苏老师帮忙解答一下,谢谢。
$z_3$明明可以看到是红线和蓝线相加,为什么不能看出依赖于$z_1,z_2$?
May 14th, 2023
苏老师您好,请问公式1根据KL散度是怎么推算出后面的表达式呢?能力不足,一直没推出来您这个结果。
May 14th, 2023
公式1只推出了这么一个结果:
\begin{align} \text{KL}(p(x, z)||q(x, z)) \\
&= \iint p(x, z) \log \frac{p(x, z)}{q(x, z)} dz dx \\
&= \iint p(x, z) \log \frac{p(x)p(z|x)}{q(x)q(z|x)} dz dx \\
&= \iint p(x, z) \log \frac{p(x)}{q(x)} dz dx + \iint p(x, z) \log \frac{p(z|x)}{q(z|x)} dz dx \\
&= \int p(x) \log \frac{p(x)}{q(x)} dx + \int p(x) \left[ \int p(z|x) \log \frac{p(z|x)}{q(z|x)} dz \right] dx \ \end{align}
抱歉,我漏了个常数,现在补上了。在你这个推导基础上,将$q(x,z)$分解为$q(x|z)q(z)$就可以得出。
August 2nd, 2023
感谢苏神,这篇博客解决了我两个一直疑惑的问题:
1 VAE的生成为什么会模糊?现在看来就是由于正则化项的影响,该项不够精细,但是如果我们将该项的影响分散到多层、多个隐变量中,就能够解决模糊问题。
2 生成模型基本都可以用隐变量来解释,用隐变量直接描述生成分布正确与否,就是GAN;用变分推断推导隐变量,间接约束生成分布正确,就是VAE;直接反解正确的隐变量,就是flow;
但是又产生了一些疑惑:
1 目前看来LVAE也好还是这里的NVAE,或者生成扩散模型,都是多层隐变量,那么单层多个隐变量能不能解决模糊问题?(Very Deep VAE说明了多层为什么有用,多个是不是有用呢?)
2 多层隐变量的求解由于需要原始消息x,由p(z1|z2)到p(z1|z2,x),就变成了自回归模型,这里的自回归模型与变分不变分有无关系?自回归模型一定是AE才能叫自回归吗?还是VAE也可以?
3 我理解一定是AE才能做回归,更进一步这里的NVAE虽然也有KL散度项,但本质上是不是还是个AE?
我想了想觉得第2,3个问题不对,VAE是AE的一种。这里用了KL散度,其实就可以叫VAE了。
单层VAE想要做得清晰,基本上都要加GAN来作为loss,所以本质上还是GAN。
March 21st, 2025
谁帮忙把公式(3)推导一下?
因为q(z)与p(z|x)的隐变量分组概率乘积的关系,是不是得对所有的z分组求积分?
你代入KL散度的积分表达式,然后$\log$将连乘变加,应该基本上都能看出来了啊。