修改Transformer结构,设计一个更快更好的MLM模型
By 苏剑林 | 2020-08-07 | 79980位读者 |大家都知道,MLM(Masked Language Model)是BERT、RoBERTa的预训练方式,顾名思义,就是mask掉原始序列的一些token,然后让模型去预测这些被mask掉的token。随着研究的深入,大家发现MLM不单单可以作为预训练方式,还能有很丰富的应用价值,比如笔者之前就发现直接加载BERT的MLM权重就可以当作UniLM来做Seq2Seq任务(参考这里),又比如发表在ACL 2020的《Spelling Error Correction with Soft-Masked BERT》将MLM模型用于文本纠错。
然而,仔细读过BERT的论文或者亲自尝试过的读者应该都知道,原始的MLM的训练效率是比较低的,因为每次只能mask掉一小部分的token来训练。ACL 2020的论文《Fast and Accurate Deep Bidirectional Language Representations for Unsupervised Learning》也思考了这个问题,并且提出了一种新的MLM模型设计,能够有更高的训练效率和更好的效果。
MLM模型 #
假设原始序列为$\boldsymbol{x}=[x_1,x_2,\dots,x_T]$,$\boldsymbol{x}\backslash \{x_i\}$表示将第i个token替换为$\text{[MASK]}$后的序列,那么MLM模型就是建模
\begin{equation}p\big(x_i, x_j, x_k, \cdots\big|\,\boldsymbol{x}\backslash \{x_i,x_j,x_k,\cdots\}\big)\end{equation}
我们说它效率低,是因为每次只能选择一小部分token来mask,比如15%,那么也就是说每个样本只有15%的token被训练到了,所以同一个样本需要反复训练多次。在BERT里边,每个样本都被mask了多遍然后存为tfrecord,训练效率低的同时还增加了硬盘空间占用。
如果训练的时候每个样本的所有token都可以作为预测目标,那么训练效率自然就能提升了。像GPT这样的单向语言模型是可以做到的,但是MLM是双向的模型,并不能直接做到这一点。为了达到这个目标,我们需要简化一下上式,假设每次只mask掉一个token,也就是要构建的分布为
\begin{equation}p\big(x_i\big|\,\boldsymbol{x}\backslash \{x_i\}\big),\,i=1,2,\dots,T\end{equation}
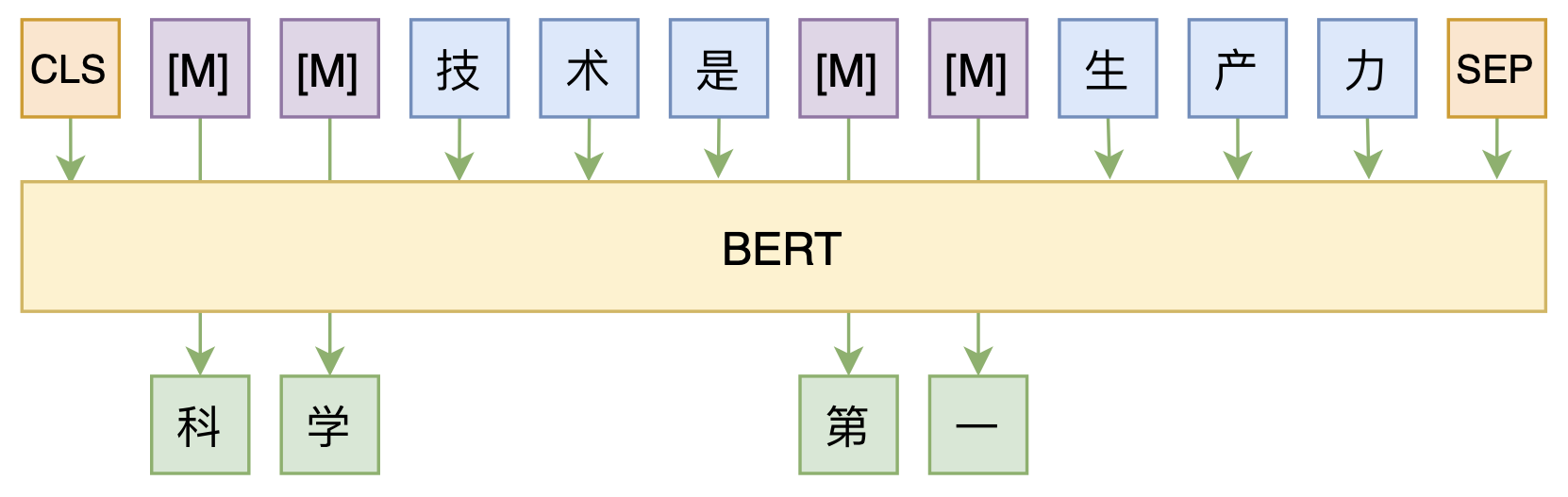
然后我们希望通过单个模型一次预测就同时得到$p(x_1|\,\boldsymbol{x}\backslash \{x_1\}),p(x_2|\,\boldsymbol{x}\backslash \{x_2\}),\dots,p(x_T|\,\boldsymbol{x}\backslash \{x_T\})$。怎么做到这一点呢?这就来到本文要介绍的论文结果了,它提出了一种称之为T-TA(Transformer-based Text Autoencoder)的设计,能让我们一并预测所有token的分布。
T-TA介绍 #
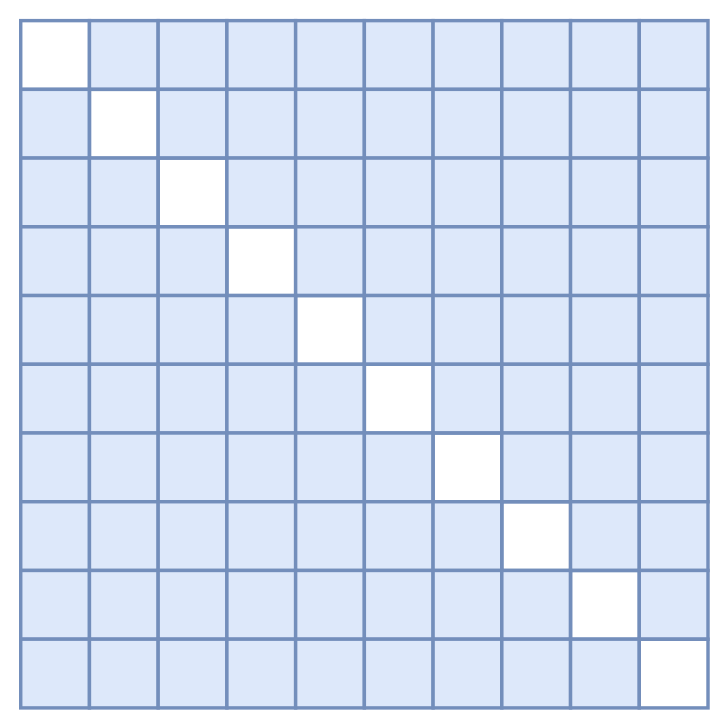
首先,我们知道Transformer的核心运算是$Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})$,在BERT里边$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$都是同一个,也就是Self Attention。而在MLM中,我们既然要建模$p(x_i|\,\boldsymbol{x}\backslash \{x_i\})$,那么第$i$个输出肯定是不能包含第$i$个token的信息的,为此,第一步要做出的改动是:去掉$\boldsymbol{Q}$里边的token输入,也就是说第一层的Attention的$\boldsymbol{Q}$不能包含token信息,只能包含位置向量。这是因为我们是通过$\boldsymbol{Q}$把$\boldsymbol{K},\boldsymbol{V}$的信息聚合起来的,如果$\boldsymbol{Q}$本身就有token信息,那么就会造成信息泄漏了。然后,我们要防止$\boldsymbol{K},\boldsymbol{V}$的信息泄漏,这需要修改Attention Mask,把对角线部分的Attention(也就是自身的)给Mask掉,如图所示。
如果还不理解这一点,我们可以从Attention的一般形式来理解:Attention的一般定义为
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i = \frac{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)\boldsymbol{v}_j}{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)}\label{eq:gen-att}\end{equation}
所以很明显,$Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i$一定跟$\boldsymbol{q}_i$有联系,所以$\boldsymbol{q}_i$绝对不能包含第$i$个token的信息;但它不一定跟$\boldsymbol{k}_i,\boldsymbol{v}_i$有联系,因为只需要当$\text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_i)=0$时$\boldsymbol{k}_i,\boldsymbol{v}_i$就相当于不存在了,因此需要Mask掉对角线部分的Attention。
但是,这种防泄漏的Attention Mask只能维持一层!也就是说即便这样做之后,$Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_j$已经融入了第$i$个token的信息了,所以从第二层开始,如果你还是以第一层的输出为$\boldsymbol{K},\boldsymbol{V}$,即便配合了上述Attention Mask,也会出现信息泄漏了。
原论文的解决很粗暴,但貌似也只能这样解决了:每一层Attention都共用原始输入为$\boldsymbol{K},\boldsymbol{V}$!所以,设$\boldsymbol{E}$为token的embedding序列,$\boldsymbol{P}$为对应的位置向量,那么T-TA与BERT的计算过程可以简写为:
\begin{equation}
\begin{array}{c}\bbox[border: 1px dashed red; padding: 5px]{\begin{aligned}&\boldsymbol{Q}_0 = \boldsymbol{E}+\boldsymbol{P}\\
&\boldsymbol{Q}_1 = Attention(\boldsymbol{Q}_0,\boldsymbol{Q}_0,\boldsymbol{Q}_0)
\\
&\boldsymbol{Q}_2 = Attention(\boldsymbol{Q}_1,\boldsymbol{Q}_1,\boldsymbol{Q}_1)
\\
&\qquad\vdots\\
&\boldsymbol{Q}_n = Attention(\boldsymbol{Q}_{n-1},\boldsymbol{Q}_{n-1},\boldsymbol{Q}_{n-1})
\end{aligned}} \\ \text{BERT运算示意图}\quad\end{array}\qquad
\begin{array}{c}\bbox[border: 1px dashed red; padding: 5px]{\begin{aligned}&\boldsymbol{Q}_0 = \boldsymbol{P}\\
&\boldsymbol{Q}_1 = Attention(\boldsymbol{Q}_0,\boldsymbol{E}+\boldsymbol{P},\boldsymbol{E}+\boldsymbol{P})
\\
&\boldsymbol{Q}_2 = Attention(\boldsymbol{Q}_1,\boldsymbol{E}+\boldsymbol{P},\boldsymbol{E}+\boldsymbol{P})
\\
&\qquad\vdots\\
&\boldsymbol{Q}_n = Attention(\boldsymbol{Q}_{n-1},\boldsymbol{E}+\boldsymbol{P},\boldsymbol{E}+\boldsymbol{P})
\end{aligned}} \\ \text{T-TA运算示意图}\quad\end{array}\end{equation}
当然残差、FFN等细节已经省略掉了,只保留了核心运算部分,预训练阶段T-TA的Attention是进行了对角线形式的Attention Mask的,如果是下游任务的微调,则可以把它去掉。
实验结果 #
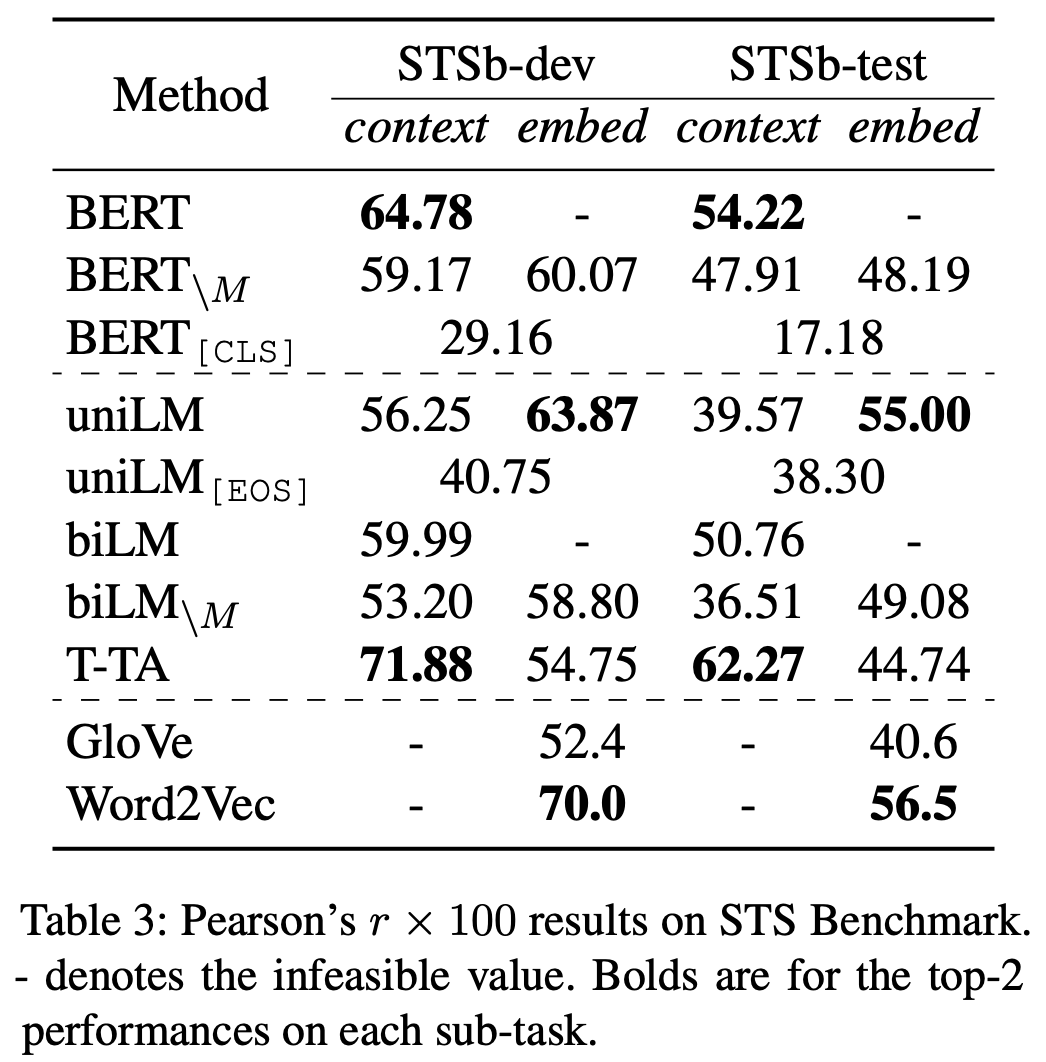
基于上述设计,T-TA它能一次性预测所有的token,所以训练效率高,并且不需要额外的$\text{[MASK]}$符号,所以实现了预训练和微调之间的一致性。但是不难理解,T-TA实则是对标准Transformer的一种简化,所以理论上它的拟合能力是变弱了。这样一收一放之下,具体表现还有没有提升呢?当然,论文的实验结果是有的。原论文做了多个实验,结果显示T-TA这种设计在同样的参数情况下基本都能媲美甚至超过标准的MLM训练出来的模型。作者还很慷慨地开源了代码,以便大家复现结果(链接)。
说到修改Transformer结构,大家可能联想到大量的GPU、TPU在并行运算。但事实上,虽然作者没有具体列出自己的实验设备,但从论文可以看到设备阵容应该不算“豪华”。为此,作者只训练了3层的T-TA,并且按照同样的模式复现了3层的MLM和GPT(也就是单向语言模型),然后对比了效果。没错,论文中所有T-TA的结果都只是3层的模型,而其中有些都超过了Base版本的BERT。所以作者生动地给我们上了一课:没有土豪的设备,也可以做修改Transformer的工作,也可以发ACL,关键是你有真正有效的idea。
个人分析 #
最后,再来简单谈谈T-TA为什么有效。读者可能会质疑,既然作者只做了3层的实验,那么如何保证在更多层的时候也能有效呢?那好,我们来从另外一个角度看这个模型。
从设计上看,对于T-TA来说,当输入给定后,$\boldsymbol{K},\boldsymbol{V}$在所有Attention层中的保持不变,变化的只有$\boldsymbol{Q}$,所以读者质疑它效果也不意外。但是别忘了,前段时候Google才提出了个Synthesizer(参考《Google新作Synthesizer:我们还不够了解自注意力》),里边探索了几种Attention变种,其中一种简称为“R”的,相当于$\boldsymbol{Q},\boldsymbol{K}$固定为常数,结果居然也能work得不错!要注意,“R”里边的$\boldsymbol{Q},\boldsymbol{K}$是彻彻底底的常数,跟输入都没关系。
所以,既然$\boldsymbol{Q},\boldsymbol{K}$为常数效果都还可以,那么$\boldsymbol{K},\boldsymbol{V}$为什么不能为常数呢?更何况T-TA的$\boldsymbol{K},\boldsymbol{V}$动态依赖于输入的,只是输入确定后它才算是常数,因此理论上来讲T-TA的拟合能力比Synthesizer的“R”模型要强,既然“R”都能好了,T-TA能好应该也是不奇怪。
当然,还是期望后续会有更深的实验结果出现。
转载到请包括本文地址:https://kexue.fm/archives/7661
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Aug. 07, 2020). 《修改Transformer结构,设计一个更快更好的MLM模型 》[Blog post]. Retrieved from https://kexue.fm/archives/7661
@online{kexuefm-7661,
title={修改Transformer结构,设计一个更快更好的MLM模型},
author={苏剑林},
year={2020},
month={Aug},
url={\url{https://kexue.fm/archives/7661}},
}










August 13th, 2020
使用XLNet那种two stream attention的形式,一个attention只有位置信息,另一个包含了上下文,使用只包含位置信息的attention来预测各个位置的token。这样行得通吗?(由于位置attention和上下文的attention因为存在交互,在多层网络的情况下同样会造成KV信息泄漏的问题?)
xlnet是不会泄露的,它每个位置能看多少信息是提前算好的,所以不会看到不应该看的
作为语言模型来说没问题,但作为mlm来说还是不够的,还是会泄漏,原因文本已经说了。
August 13th, 2020
xlnet的做法不就是正确解决了mask导致训练效率低的问题么。。。xlnet是有mask的,双流就是一个带自己,一个不带自己信。那这篇论文的意义在哪呢?
xlnet只是一个单向语言模型,虽然它的顺序可以随机,但选定顺序后它就是单向的。而这篇文章要的就是mlm。其次,transformer-xl太丑,所以xlnet也没什么意思,不妨碍新的研究。
“那这篇论文的意义在哪呢?”,我很疑惑怎么会提出这么奇怪的问题,哪怕T-TA的效果跟xlnet一样,甚至退一步说就算T-TA效果还不如xlnet,那么它就没有存在意义了么?新的思想本就应该好好学习,何况这两者又不是互为替代品,没有取代之说。
September 10th, 2020
可以"R"里边的Q,K虽然是常数 , 但是却是可以训练的 , 跟这里的只变化Q , 而K,V一直不变 , 还是有区别的吧
K,V是输入的Embedding序列,Embedding层是可训练的。
此外,“R”里边的Q,K虽然是可训练的,但是训练完成之后,所有的输入公用一个Q,K;T-TA里边的K,V则是动态依赖于输入(只是交互程度没那么深)。从这个角度来看,其实T-TA的拟合能力应当要比R强。
September 25th, 2020
可以看看icml的这篇paper,同样的想法,用来做autoregressive的翻译都不掉点的https://arxiv.org/abs/2001.05136
谢谢推荐。当时略微看过这篇文章,也看过香侬科技的解读,不过最终还是没提起兴趣来。
October 30th, 2022
[...]然而,随着研究的深入,研究人员发现不止 BERT 的 Encoder 很有用,预训练用的 MLM 本身也很有用。比如论文《BERT has a Mouth, and It Must Speak: BERT as a Markov Random Field Language Model》指出 MLM 可以作为一般的生成模型用,论文《Spelling Error Correction with Sof[...]
January 21st, 2024
想請教一下,你在復現實驗的時候,是同一個樣本,每次隨機 Mask ,反覆訓練嗎?還是一個樣本從一開始 MASK 給定之後就不再動了?
我最近嘗試復現,發現這個問題:如果每次都隨機MASK同一句話,反覆訓練多次,那幾個epoch後,模型是不是就相當於看過那整句話,比方說只要看到某個符號出現在某個位置上,就能推測MASK的字是甚麼,而無須真的理解字義?這樣就變成像是overfitting了。
似乎比較正確的做法是,在 preprocessing 的時候隨機 MASK ,後面就不再改變了。這樣一來,不論反覆訓練幾次,都不會因此拼湊出整個句子,不會在其他epoch裡面看到同一個句子MASK其他字。還是其實沒有差?
我目前的評估方法是拿沒有被 Mask 的 token 來當作 testing set,而有 Mask 的token 就是training set,看testing accuracy 有沒有成長。但如果同一句話套用不同MASK重複使用多次的話,就相當於我的 testing set 混入了training set的資料。如此一來,沒有被mask的token 預測準確率就失去意義了。在inference的時候,我們是拿一句沒看過的句子輸入,希望沒有MASK的地方應該也要能夠正確還原,才能代表該句子。所以訓練時,用沒有 mask 的部分當作 testing 應該是符合 inference 的情況的。
或者應該是這樣:一開始選出的15% 就是training set,剩下的85%是testing set。然後在training set中,80% 被mask、10%隨機、10%不變,但是在這training set裡面,mask、隨機、不變的token 是可以每次都不同的,這樣一來,剩下的85% testing set 就不會混入training set的答案,而可以當作評估的標準。
不曉得你們實際上是不是這樣操作?
另外,我發現80% mask是有道理的。主要是因為Transformer 中 multihead attention 輸出有加上 input token embedding 的殘差連結。當 MASK 比例太小時,模型可以讓 attention 輸出同一個值,直接使用input token embedding 來做預測,等於沒有利用到上下文 attention 的資訊。所以只能夠透過加大MASK比例,來強迫模型透過 attention head 學習上下文資訊。
但是我在小資料上,MASK太大就幾乎沒東西可學了。若拿掉 input token embedding 的殘差連結,就能讓模型完全透過attention 學習,但是拿掉殘差連結後,又沒辦法訓練深層。此時,我發現RealFormer https://kexue.fm/archives/8027 這篇提供了另一條路徑,將殘差加在attention score上。
但是就像我在留言中 https://kexue.fm/archives/8027/comment-page-2#comment-23539 說的,這種殘差有可能會退化成只使用第一層。除非在score中加上一些random noise,才可讓每一層學到不太一樣的score。
然而,實驗結果顯示,就算加了 random noise 或 dropout,將殘差加在attention score上的這種方法,每一層的attention 還是會趨同,這就違背了我想看每一層不同attention 變化的初衷。
最近想到,也許可以藉由變動 MASK ratio (0.4~0.8) 來達到避免模型直接使用 input token embedding 的殘差連結。當MASK ratio=0.4的時候,模型幾乎可以使用殘差連結直接預測,而不透過attention;但當MASK ratio=0.8時,模型沒辦法只透過殘差連結來預測答案,此時就需要來自 attention 的資訊。隨機的變動MASK ratio,也許可以讓模型學會更多使用attention 的資訊。
目前在測試這種方法能否學出比較有意義的attention。
實驗結果,變動 MASK ratio 還是不能避免 attention 對每個字輸出一樣的值。
後來我又想到,既然我希望對每個字不同,那就是要增加 attention weights 的diversity! 定義 diversity 為 attention weights 的 std,計算 [query1,query2,query3,...] 對 value1 的std,即 std([attn11,attn21,attn31,...])=div1, 對 value2 的std,即std([attn12,attn22,attn32,...])=div2,...以此類推。然後在loss中加入平均div即可。這是在softmax的情況。
但是我是用sigmoid,每個attention weight 是獨立的0~1分布,沒有沿著序列方向的歸一化。因此,有可能出現 [1111100000] 這種std值很高,但對每個 value 都是 [1111100000] 這種分布。因此,我希望增加 value 這個方向的std 的 diversity,也就是std的std。第一個std是沿query方向,算出來後再延value方向算一次std,然後取平均,加到loss裡。
實驗結果顯示,確實能夠避免每個字都輸出相同的attention weights。這個方法應該也可以用來鼓勵 RealFormer 中的每次層輸出不同的 attention weights,只是手動調整loss 的比例確實有些麻煩...。
我發現在loss中加入attention weights分別沿著兩個方向的 std of stds 非常關鍵!他可以鼓勵 model 產生每個 token 不同的 attention weight,從而讓model必須利用到 attention 而非只用到殘差連線的資訊。這給小資料預訓練減少使用MASK開啟了一條路!
不同於你在 https://kexue.fm/archives/9889 這篇說的稀疏性。稀疏性只能告訴我們關注到少數幾個token的能力,但並沒有告訴我們每個token 需要關注的資訊不同。所以有可能很稀疏,但每個token 關注的部分幾乎都相同,例如都集中在[cls], 逗號、句號等。
而 token 間的 diversity 則可以告訴我們 token 表示方法的多樣性。若說self-attention 是透過 attention weight 來對整個 sequence 加權得到 token 表示,那麼token對token 的attention weight應該要儘量多元,才能得到每個token不同的表示。
傳統的 Transformer,attention weight 是透過大量資料學出來的,其實並沒有辦法保證token表示的多樣性,只能夠過增加層數並加大MASK 比率,期待它自動學出多樣性。
但是如果在loss中顯式加入attention weights 的diversity,以 std of stds 來衡量,模型就會非常有效地為每個token產生不同的表示。這樣就避免模型跳過attention 直接使用殘差連結,從而可以減少MASK的比率。(我甚至認為也許可以不用MASK,因為 diversity 會鼓勵模型混到其他 token。)
我甚至認為 Linear Attention 或 Flash 等非歸一化的 attention,也可以透過加入這個 attention diversity loss 來提升在小資料上的訓練效果。
@Allen7575|comment-23622
我还是不大理解你说的“attention对每個字输出一样的值”具体含义是什么?还是指一对多的建模没有输出随机性的结果?或者是说realformer的attention矩阵在最后趋同?
顺便说,realformer的attention矩阵在最后只是趋同,且趋于one hot,但不一定是趋于第一层的attention,所以你说的“退化为只使用第一层”是不成立的。
我是随机mask的,可能出现你说的问题。但只要数据量够多,这个问题就可以忽略。
从压缩的角度想,我当时训练MLM的数据少则几十GB,多则上百GB,但模型权重大小也就是300来MB(1亿参数量),所以数据远远是充足的,不用担心这种过拟合问题,所以后来dropout都直接去掉了。
確實,不過我是想要用在小資料上,所以確實可能需要這層考慮