科学空间|Scientific Spaces

最近一直在考虑一些自然语言处理问题和一些非线性分析问题，无暇总结发文，在此表示抱歉。本文要说的是对于一阶非线性差分方程（当然高阶也可以类似地做）的一种摄动格式，理论上来说，本方法可以得到任意一阶非线性差分方程的显式渐近解。

非线性差分方程

对于一般的一阶非线性差分方程
$$\begin{equation}\label{chafenfangcheng}x_{n+1}-x_n = f(x_n)\end{equation}$$
通常来说，差分方程很少有解析解，因此要通过渐近分析等手段来分析非线性差分方程的性质。很多时候，我们首先会考虑将差分替换为求导，得到微分方程
$$\begin{equation}\label{weifenfangcheng}\frac{dx}{dn}=f(x)\end{equation}$$
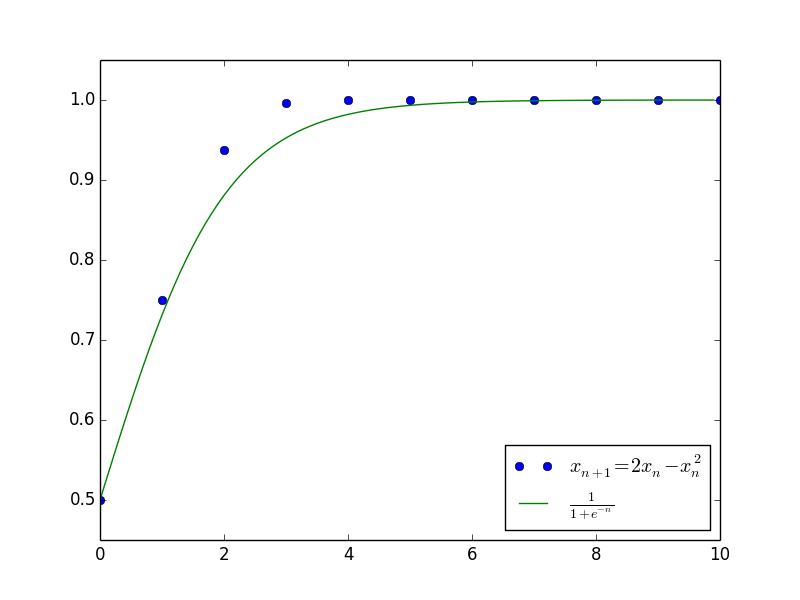
作为差分方程$\eqref{chafenfangcheng}$的近似。其中的原因，除了微分方程有比较简单的显式解之外，另一重要原因是微分方程$\eqref{weifenfangcheng}$近似保留了差分方程$\eqref{chafenfangcheng}$的一些比较重要的性质，如渐近性。例如，考虑离散的阻滞增长模型：
$$\begin{equation}\label{zuzhizengzhang}x_{n+1}=(1+\alpha)x_n -\beta x_n^2\end{equation}$$
对应的微分方程为（差分替换为求导）：
$$\begin{equation}\frac{dx}{dn}=\alpha x -\beta x^2\end{equation}$$
此方程解得
$$\begin{equation}x_n = \frac{\alpha}{\beta+c e^{-\alpha n}}\end{equation}$$
其中$c$是任意常数。上述结果已经大概给出了原差分方程$\eqref{zuzhizengzhang}$的解的变化趋势，并且成功给出了最终的渐近极限$x_n \to \frac{\alpha}{\beta}$。下图是当$\alpha=\beta=1$且$c=1$（即$x_0=\frac{1}{2}$）时，微分方程的解与差分方程的解的值比较。

差分方程的摄动法1

现在的问题是，既然微分方程的解可以作为一个形态良好的近似解了，那么是否可以在微分方程的解的基础上，进一步加入修正项提高精度？

点击阅读全文...

换一个小参数

比较《高斯型积分的微扰展开（一）》和《高斯型积分的微扰展开（二）》两篇文章，我们可以得出关于积分
$$\int_{-\infty}^{+\infty} e^{-ax^2-\varepsilon x^4} dx\tag{1}$$
的两个结论：第一，我们发现类似$(4)$式的近似结果具有良好的性质，对任意的$\varepsilon$都能得到一个相对靠谱的近似；第二，我们发现在指数中逐阶展开，得到的级数效果会比直接展开为幂级数的效果要好。那么，两者能不能结合起来呢？

我们将$(4)$式改写成
$$\int_{-\infty}^{+\infty} e^{-ax^2-\varepsilon x^4} dx\approx\sqrt{\frac{2\pi}{a+\sqrt{a^2+6 \varepsilon}}}=\sqrt{\frac{\pi}{a+\frac{1}{2}\left(\sqrt{a^2+6 \varepsilon}-a\right)}}\tag{6}$$

点击阅读全文...

为什么第二篇姗姗来迟？

其实要写这系列之前，我已经构思好了接下来几篇的内容，本来想要自信地介绍自己想到的一些积分展开的技巧；而且摄动法我本身就比较熟悉，所以正常来说不会这么迟才有第二篇。然而，在我写完第一篇，准备写第二篇的期间，我看到了知乎上的这篇回复：
http://www.zhihu.com/question/24735673

这篇文章大大地拓展了我对级数的认识。里边谈及到了积分的展开是一个渐近级数。这让我犹豫了，怀疑这系列有没有价值，因为渐近级数意味着不管怎样的展开技巧，得到的级数收敛半径都是0。

后来再想想，就算是渐近级数，也有改进的空间，有加速收敛的方法，所以我想我这几篇文章，应该还有一点点意义吧，还可以顺便介绍一下渐近级数和奇点的相关理论。嗯，就这么办吧。

点击阅读全文...

前段时间在研究费曼的路径积分理论，看到路径积分的微扰方法，也就是通过小参数展开的方式逐步逼近传播子。这样的技巧具有非常清晰的物理意义，有兴趣了解路径积分以及量子力学的读者，请去阅读费曼的《量子力学与路径积分》。然而从数学角度看来，这种逼近的技巧实际上非常粗糙，收敛范围和速度难以得到保证。事实上，数学上发展了各种各样的摄动技巧，来应对不同情况的微扰。下面我们研究积分
$$\int_{-\infty}^{+\infty} e^{-ax^2-\varepsilon x^4} dx\tag{1}$$
或者更一般地
$$\int_{-\infty}^{+\infty} e^{-ax^2-\varepsilon V(x)} dx\tag{2}$$
路径积分的级数展开比它稍微复杂一些，但是仍然是类似的形式。

点击阅读全文...

Mathieu方程

在文章《有质动力：倒立单摆的稳定性》中，我们分析了通过高频低幅振荡来使得倒立单摆稳定的可能性，并且得出了运动方程
$$l\ddot{\theta}+[h_0 \omega^2 \cos(\omega t)-g]\sin\theta=0$$

由此对单摆频率的下限提出了要求$\omega \gg \sqrt{\frac{g}{h_0}}$。然而，那个下限只不过是必要的，却不是充分的。如果要完整地分析该单摆的运动方程，最理想的方法当然是写出上述常微分方程的解析解。不过很遗憾，我们并没有办法做到这一点。我们只能够采取各种近似方法来求解。近似方法一般指数值计算方法，然后笔者偏爱的是解析方法，也就是说，即使是近似解，也希望能够求出近似的解析解。

点击阅读全文...

开始之初，我偶然在图书馆看到了一本名为《超越摄动：同伦分析方法导论》，里边介绍了一种求微分方程近似解的新方法，关键是里边的内容看起来并不是十分难懂，因此我饶有兴致地借来研究了。果然，这是一种非常有趣的方法，在某种意义上来说，还是非常简洁的方法。这解决了我一直以来想要研究的问题：用傅里叶级数来近似描述单摆运动的近似解。当然，它带给我的冲击不仅仅是这些。为了得出周期解，我又同时研究了各种摄动方法的技巧，如消除长期项的PL(Poincaré–Lindstedt)方法。这同时增加了我对各种近似解析方法的了解。从开学到现在快三周的时间，我一直都在研究这些问题。

点击阅读全文...

微分方程领域大放光彩

虽然微分方程在各个计算领域都能一展才华，不过它最辉煌的光芒无疑绽放于微分方程领域，包括常微分方程和偏微分方程。海王星——“笔尖上发现的行星”——就是摄动法的著名成果，类似的还有冥王星的发现。天体力学家用一颗假设的行星的引力摄动来解释已知行星的异常运动，并由此反推未知行星的轨道。我们已不止一次提到过，一般的三体问题是混沌的，没有精确的解析解。这就要求我们考虑一些近似的方法，这样的方法发展起来就成为了摄动理论。

跟解代数方程一样，摄动法解带有小参数或者大参数的微分方程的基本思想，就是将微分方程的解表达为小参数或大参数的幂级数。当然，这是最直接的，也相当好理解，不过所求得的级数解有可能存在一些性态不好的情况，比如有时原解应该是一个周期运动，但是级数解却出现了诸如$t \sin t$的“长期项”，这是相当不利的，因此也发展出各种技巧来消除这些项。可见，摄动理论是一门应用广泛、集众家所大成的实用理论。下面我们将通过一些实际的例子来阐述这个技巧。

点击阅读全文...

为了让大家更加熟悉摄动法的基本步骤，本文再讲一个用摄动法解代数方程的例子。这是从实际研究中出来的：
$$\begin{eqnarray*} x=\frac{k(1+k^2+k^4+l^2)}{2(1+k^2)^2} \\ k=\frac{dy}{dx}\end{eqnarray*} $$

这是一道微分方程。要求解这道方程，最好的方法当然是先从第一式解出$k=k(x)$的形式然后再积分。但是由于五次方程没有一般的显式解，所以迫使我们要考虑近似解。当然，一般来说熟悉mathematica的人都会直接数值计算了。我这里只考虑摄动法。

我们将原方程变为下面的形式：
$$x=\frac{k}{2}[1+\frac{l^2}{(1+k^2)^2}]$$

点击阅读全文...