从梯度最大化看Attention的Scale操作

我们知道，Scaled Dot-Product Attention的Scale因子是$\frac{1}{\sqrt{d}}$，其中$d$是$\boldsymbol{q},\boldsymbol{k}$的维度。这个Scale因子的一般解释是：如果不除以$\sqrt{d}$，那么初始的Attention就会很接近one hot分布，这会造成梯度消失，导致模型训练不起来。然而，可以证明的是，当Scale等于0时同样也会有梯度消失问题，这也就是说Scale太大太小都不行。

那么多大的Scale才适合呢？$\frac{1}{\sqrt{d}}$是最佳的Scale了吗？本文试图从梯度角度来回答这个问题。

已有结果 #

在《浅谈Transformer的初始化、参数化与标准化》中，我们已经推导过标准的Scale因子$\frac{1}{\sqrt{d}}$，推导的思路很简单，假设初始阶段$\boldsymbol{q},\boldsymbol{k}\in\mathbb{R}^d$都采样自“均值为0、方差为1”的分布，那么可以算得
\begin{equation}\mathbb{V}ar[\boldsymbol{q}\cdot\boldsymbol{k}] = d\end{equation}
于是我们将$\boldsymbol{q}\cdot\boldsymbol{k}$除以$\sqrt{d}$，将Attention Score的方差变为1。也就是说，之前的推导纯粹是基于“均值为0、方差为1”就会更好的信仰来得到的结果，但没有解释让Attention Score的方差为1，也没有评估$\frac{1}{\sqrt{d}}$是否真的就解决了梯度消失问题。

当然，从已有的实验来看，$\frac{1}{\sqrt{d}}$至少一定程度上是缓解了这个问题，但这毕竟是实验结果，我们还是希望能从理论上知道“一定程度”究竟是多少。

计算梯度 #

既然涉及到了梯度，那么最好的办法就是把梯度算出来，然后定一个优化目标。设$p_i = e^{\alpha s_i}/Z$，$i \in \{1,2,...,n\}$，$Z=\sum_i e^{\alpha s_i}$是归一化因子，那么可以直接算得：
\begin{equation}\frac{\partial p_i}{\partial s_j} = \left\{\begin{aligned}
\alpha(p_i - p_i^2),&\quad i=j\\
-\alpha p_i p_j,&\quad i\neq j
\end{aligned}\right.\end{equation}
或者可以简写成$\partial p_i/\partial s_j = \alpha(p_i\delta_{i,j} - p_i p_j)$。很明显，当$\alpha\to 0$时梯度为0；当$\alpha\to\infty$时，$p_i$之中只有一个1、其余都是0（假设$s_i$中只有唯一的最大值），梯度也是0。

为了更有利于优化，我们应该选取$\alpha$使得梯度尽可能最大化。为此，我们以L1范数作为梯度大小的度量：
\begin{equation}\frac{1}{2}\left\Vert\frac{\partial p}{\partial s}\right\Vert_1=\frac{1}{2}\sum_{i,j}\left|\frac{\partial p_i}{\partial s_j}\right|=\frac{1}{2}\sum_i \alpha(p_i - p_i^2) + \frac{1}{2}\sum_{i\neq j} \alpha p_i p_j = \alpha\left(1 - \sum_i p_i^2\right)\label{eq:target}\end{equation}
从最后的结果不难猜到，之所以选择L1而不是其他的根本原因是因为L1范数的计算结果足够简单。值得指出的是，这里出现了$\sum_i p_i^2$，它本质上就是我们在《如何度量数据的稀疏程度？》介绍过的“Rényi熵”，跟信息熵类似，它也是不确定性的一种度量。

有了优化目标后，我们就可以着手进行最大化了。注意$p_i$的定义里边也包含$\alpha$，所以这是一个关于$\alpha$复杂的非线性目标，看上去求解析解是不可能的，但我们可以针对一些特殊例子求近似解。

正态分布 #

首先，我们可以接着前面的结果来做，当我们通过除以$\sqrt{d}$使得Attention Score的均值为0、方差为1后，我们就可以近似假设$s_i\sim\mathcal{N}(0,1)$，然后再求$\alpha$的最优解，如果$\alpha=1$，那么就意味着原来的$\frac{1}{\sqrt{d}}$就是最优的Scale比例了，否则$\frac{\alpha}{\sqrt{d}}$才是最佳的Scale比例。

我们用期望去估计求和
\begin{equation}\sum_i p_i^2 = \frac{\sum_i e^{2\alpha s_i}}{\left(\sum_i e^{\alpha s_i}\right)^2} = \frac{\frac{1}{n}\sum_i e^{2\alpha s_i}}{n\left(\frac{1}{n}\sum_i e^{\alpha s_i}\right)^2} \approx \frac{\mathbb{E}_s[e^{2\alpha s}]}{n\left(\mathbb{E}_s[e^{\alpha s}]\right)^2}\label{eq:approx}\end{equation}
对于服从标准正态分布的$s$，我们有
\begin{equation}\mathbb{E}_s[e^{\alpha s}] = \int \frac{1}{\sqrt{2\pi}}e^{-s^2/2}e^{\alpha s} ds = e^{\alpha^2 / 2}\label{eq:normal}\end{equation}
代入上式，然后代入式$\eqref{eq:target}$，得到
\begin{equation}\alpha\left(1 - \sum_i p_i^2\right)\approx\alpha\left(1 - \frac{e^{\alpha^2}}{n}\right)\end{equation}
最后的近似，虽然已经足够简化了，但其实也不容易求出最大值来。不过无妨，我们可以遍历一些$n$，然后数值求解出取最大值时的$\alpha^*$，这样我们就大致能看到$\alpha^*$与$n$的关系了，Mathematica的参考代码如下：

(*定义函数*)
f[a_, n_] := a*(1 - Exp[a^2]/n)
(*找到函数的最大点对应的a*)
FindArg[n_] := 
 Module[{a}, a = a /. Last@NMaximize[{f[a, n], a > 0}, a][[2]]; a]
(*给定n的范围*)
nRange = 40*Range[1, 500];
(*求出每个n对应的a*)
args = FindArg /@ nRange;
(*画出a与n的函数图像*)
ListLinePlot[{args, 0.84*Log[nRange]^0.5}, 
 DataRange -> {40, 20000}, AxesLabel -> {"n", "a"}, 
 PlotLegends -> {Row[{"a", Superscript["", "*"]}], 
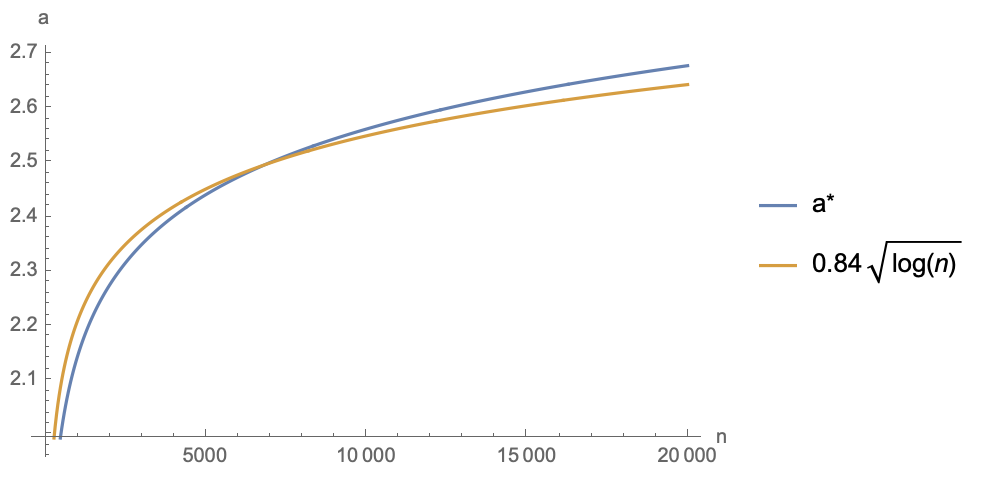
   TraditionalForm[HoldForm[0.84*Sqrt[Log[n]]]]}]

经过拟合，笔者发现一定范围内最优点$\alpha^*$与$n$大致满足$\alpha\approx 0.84\sqrt{\log n}$的关系，所以也已经将对应的近似函数一并画在一起：

标准正态分布的最优alpha与n关系

可以看到，在相当大的一个范围内，$\alpha^*$的最优值都在$2\sim 3$之间，所以折中一下的话，盲取$\frac{2.5}{\sqrt{d}}$作为Attention的Scale因子理论上更有利于优化。

余弦分布 #

现在我们考虑另一个不那么常见的例子：当我们对$\boldsymbol{q},\boldsymbol{k}$都做$l_2$归一化变成单位向量后，它们的内积就变成了夹角余弦，即$s_i$近似服从$d$维空间中的两个随机向量的夹角余弦分布。这个分布可能有些读者并不熟悉，但之前我们在《n维空间下两个随机向量的夹角分布》已经探讨过，它的概率密度具有形式
\begin{equation}p(s)\propto (1-s^2)^{(d-3)/2}\end{equation}

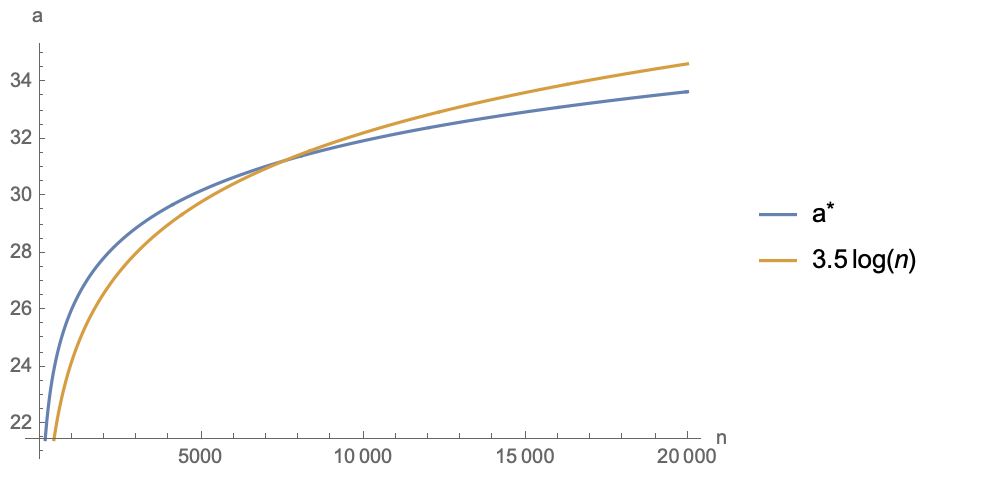
看上去并不复杂，但事实上这个形式比正态分布难处理得多，主要是$\mathbb{E}_s[e^{\alpha s}]$已经不像式$\eqref{eq:normal}$那样可以用初等函数表达出来了，不过对于Mathematica数值求解来说问题不大。跟上一节同样的思路，近似式$\eqref{eq:approx}$也同样适用，先数值求解最大值，然后再拟合，结果如下（图中$d=128$，$\alpha^*$跟$d$相关）：

余弦分布的最优alpha与n关系

可以看到，$\alpha^*$与$3.5\log n$拟合得也不错（换一个$d$的话，$3.5$这个系数会变化）。可以看到，在一个相当大的范围内，$\alpha^*$都是$25\sim 35$之间，所以如果用$\cos$值作为Attention Score的话，就需要乘以一个$25\sim 35$之间的Scale，才能使得模型比较容易训下去。这同时也解释了为什么我们在用$\cos$值构建Softmax分布（比如AM-Softmax、SimCSE等）时，需要在$\cos$之后乘上一个30左右的Scale了，因为不乘是很难训得动模型的。

对于不同的$d$和$n$，读者可以自行修改下面的代码计算最优$\alpha$：

(*定义函数*)
h[a_] := 
 Integrate[Exp[a*s]*(1 - s^2)^((d - 3)/2), {s, -1, 1}, 
  Assumptions -> {d > 10}]
g[a_] = h[a]/h[0] // FullSimplify;
f[a_, n_] := a (1 - g[2*a]/g[a]^2/n) /. {d -> 128}
(*找到函数的最大点对应的a*)
FindArg[n_] := 
 Module[{a}, a = a /. Last@NMaximize[{f[a, n], a > 0}, a][[2]]; a]
(*给定n的范围*)
nRange = 40*Range[1, 500];
(*求出每个n对应的a*)
args = FindArg /@ nRange;
(*画出a与n的函数图像*)
ListLinePlot[{args, 3.5*Log[nRange]}, 
 DataRange -> {40, 20000}, AxesLabel -> {"n", "a"}, 
 PlotLegends -> {Row[{"a", Superscript["", "*"]}], 
   TraditionalForm[HoldForm[3.5*Log[n]]]}]

相关思考 #

本文的标题和结果，尤其是余弦分布中$\alpha$近似正比于$\log n$的结果，很容易让我们联想到另一篇讨论Attention Scale的文章《从熵不变性看Attention的Scale操作》。事实上，两篇文章的联系确实存在，本文的优化目标$\eqref{eq:target}$出现了“Rényi熵”，而“熵不变性”的熵指的是香侬信息熵，两者的性质很大程度上是一致的。最大化式$\eqref{eq:target}$使得它进入了一个“缓变”的区域，这意味着“Rényi熵”关于$n$的变化是很慢的，也意味着信息熵关于$n$的变化是很慢的，这就约等于熵不变性。

此外，对于双向Attention（Encoder）来说，假设训练样本长度相同，那么$n$就是一个常数，我们可以根据$n$算得相应的最优$\alpha$，然后固定在模型中即可；但是对于单向Attention（Decoder）来说，每个token的$n$实际上都不一样（位置id加1），所以理论上无法做到对所有token都最大化式$\eqref{eq:target}$，不过由于$\alpha^*$关于$n$的变化较慢，所以取一个差不多的值就行了，比如可以取$n=L_{\max} / 2$，这样对大部分token的梯度都比较友好了。

文章小结 #

本文从梯度的角度探讨了Attention Scale因子的选择问题。众所周知，关于这个Scale因子的“标准答案”是$\frac{1}{\sqrt{d}}$，但其推导过程中并没有讨论到它的最优性问题，所以笔者定义了一个Softmax梯度的优化目标，从最大化该目标的角度探讨了Scale因子的最优值。相关结果既可以用来改进Attention的Scale因子，也可以用来解释$\cos$相似度的对比学习的温度参数。

转载到请包括本文地址：https://kexue.fm/archives/9812

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。