科学空间|Scientific Spaces

约翰与他同时代的110位学者有通信联系，进行学术讨论的信件约有2500封，其中许多已成为珍贵的科学史文献，例如同他的哥哥雅各布以及莱布尼茨、惠更斯等人关于悬链线、最速降线（即旋轮线）和等周问题的通信讨论，虽然相互争论不断，特别是约翰和雅各布互相指责过于尖刻，使兄弟之间时常造成不快，但争论无疑会促进科学的发展，最速降线问题就导致了变分法的诞生。

有意思的是,1690年约翰·伯努利的哥哥雅可比·伯努利曾提出过悬链线问题向数学界征求答案。即：

固定项链的两端，在重力场中让它自然垂下，求项链的曲线方程.

吊桥上方的悬垂钢索，挂着水珠的蜘蛛网，电杆间的电线都是悬链线。伽利略最早注意到悬链线，猜测悬链线是抛物线。1691年莱布尼兹、惠更斯以及约翰·伯努利各自得到正确答案，所用方法是诞生不久的微积分。

点击阅读全文...

自由落体公式-示意图

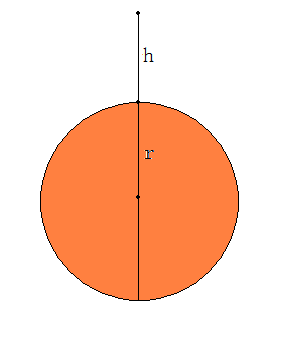
自由落体的一般定义是：只考虑吸引天体和被吸引天体的引力因素，忽略其他的运动和大气摩擦等因素，物体从静止（相对于吸引天体）开始接近吸引天体的运动。根据这个定义，假设地球为一个均匀球体，半径为r，质量为M，物体从距离地表h高度处自由落下。求落到地面的时间t，或者根据时间t求h。

令s为t时刻物体左右下落的物体与地表的距离，忽略物体的小质量，那么可以列出微分方程：
$$\frac{d^2 s}{dt^2}=-\frac{GM}{(r+s)^2}\tag{1}$$并且初始条件是$t=0,s=h,\dot{s}=v=0$

在实际应用中，我们不必求出这道微分方程的精确解，因为这个解极其麻烦，在之前曾经讨论过。我们只需要求出一个有足够精确度的近似解就行。

点击阅读全文...

一枚炮弹以速度$v_0$向上射出，只考虑重力因素，请问炮弹到达多远的距离后就会开始自由下落？

大炮的发射

对于这个问题，我们首先采取的是高中生的做法。考虑地球重力，也就是说炮弹在做加速度为-g（-9.8m/s²）的匀变速运动。根据公式$v_t^2-v_0^2=2as$，可得$s=\frac{v_0^2}{2g}$。
此即炮弹能够走得最远距离。

但是看了这条式子，我们会发现，这个“距离”始终是有限的。换一句话说，只要$v_0$不趋于无穷大，s就不会无穷大。但是我们还听到过牛顿这样说过：假如炮弹以某个速度（就是我们现在所所说的第二宇宙速度）飞离地球，它就永远不会回来了。两者不是矛盾吗？

点击阅读全文...

之前在这篇文章中，我们使用过一个牛顿引力场中的自由落体公式：
$t=\sqrt{\frac{r_0}{2GM}}{r_0 \cdot arctg \sqrt{\frac{r_0 -r}{r}}+\sqrt{r(r_0 -r)}}$——（1）

我们来尝试一下推导出这个公式来。同时，站长在逐渐深入研究的过程中，发现微分方程极其重要。以前一些我认为不可能解决的问题，都用微分方程逐渐解决了。在以后的文章里，我们将会继续体验到微分方程的伟大魔力！因此，建议各位有志研究物理学的朋友，一定要掌握微分方程，更加深入的，需要用到偏微分方程！

首先，质量为m的物理在距离地心r处的引力为$\frac{GMm}{r^2}$，根据牛顿第二定律F=ma，自然下落的物体所获得的加速度为$\frac{GM}{r^2}$。假设物体从距离地心r开始向地心自由下落，求位移s关于t的函数s=s(t).

点击阅读全文...

在初中或高中，自由落体试验简单地用这个公式来描述出来：
$$s=1/2 g t^2$$
其中$g=9.8m//s^2$，等于1kg物体在地球表面所受的重力。
但是这个公式很明显有一个问题，就是实际上在地球，g不是恒定的，会随着距离（即海拔高度）的变化而变化，上述公式能够在一定范围内描述自然落体运动。但是当距离很大时，公式便失效了。

点击阅读全文...