一个二值化词向量模型，是怎么跟果蝇搭上关系的？

可能有些读者最近会留意到ICLR 2021的论文《Can a Fruit Fly Learn Word Embeddings?》，文中写到它是基于仿生思想（仿果蝇的嗅觉回路）做出来的一个二值化词向量模型。其实论文的算法部分并不算难读，可能整篇论文读下来大家的最主要疑惑就是“这东西跟果蝇有什么关系？”、“作者真是从果蝇里边受到启发的？”等等。本文就让我们来追寻一下该算法的来龙去脉，试图回答一下这个词向量模型是怎么跟果蝇搭上关系的。

BioWord #

原论文并没有给该词向量模型起个名字，为了称呼上的方便，这里笔者就自作主张将其称为“BioWord”了。总的来说，论文内容大体上有三部分：

1、给每个n-gram构建了一个词袋表示向量；

2、对这些n-gram向量执行BioHash算法，得到所谓的（二值化的）静态/动态词向量；

3、“拼命”讲了一个故事。

其中BioHash我们稍后再介绍，总之就是一个现成的向量二值化算法。从这三点可以看出，其实整个词向量模型本身跟仿生、果蝇并没有明显的关联，就算有关系，也应该是里边的BioHash算法的关系，但这篇论文又不是提出BioHash算法的，因此说过多仿生方面的东西，就显得有点牵强了。下面再来详细解释一下这几点。

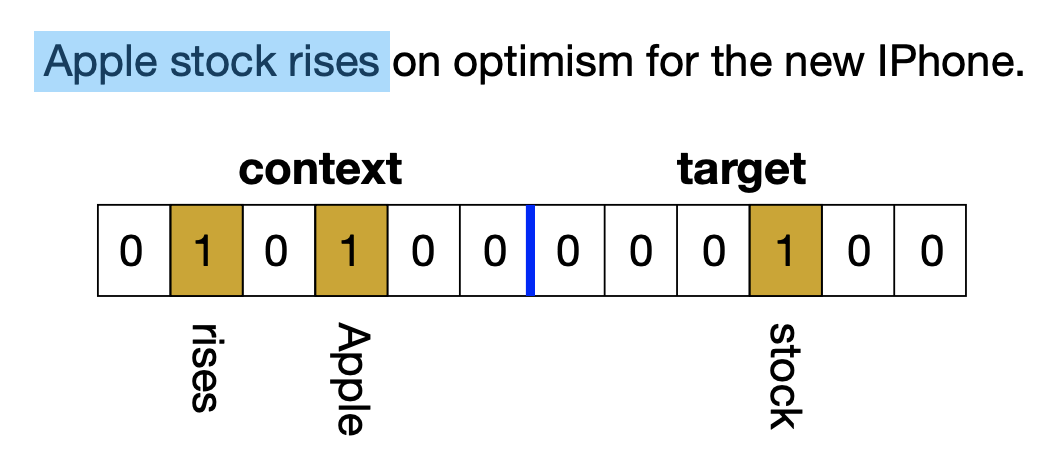
首先，给每个n-gram构建一个词袋表示向量，这个做法很朴素，结果是一个$2V$维的二值向量（即0/1向量），其中$V$是词表大小。如下图所示，前$V$维表示上下文部分，1表示上下文出现了这个词；后$V$维就是一个one hot向量，表示中心词。然后，作者对BioHash算法做了一点调整（但没有说清楚为什么这样修改，笔者也看不出如何理解这个修改），BioHash之后，每个n-gram的向量就映射为了一个$K$维的0/1向量，其中每个向量有（固定数目的）$k$个1。

最后，为什么我说作者“拼命”讲了一个故事呢？第一，前面说了，说过多仿生方面的东西显得牵强；第二，作者将BioWord跟Word2Vec、Glove等词向量模型比较，效果基本上都不如它们的；第三，至于作为一种词向量二值化算法，BioWord的效果跟已有的RandExp、LSH等相比也没有什么优势。如果只是这样那还好，但是让人觉得更尴尬的是，作者还强行跟BERT对比来突出自己的“优势”。

作者先是引入了静态/动态词向量的说法，如果词袋向量中前$V$维全是0，那么映射后的$K$维向量就是该词的静态词向量，如果词袋向量中前$V$维是依赖上下文，那么就称映射后的$K$维向量是该词的（类似BERT那样的）动态词向量。但这概念实在是难登大雅之堂，照这样说，哪怕是Word2Vec，求个上下文的平均词向量拼接到中心词向量上，也是一个动态词向量了，但这样无非就是个谈资而已，实验结果也没显示出有什么优势。还有，作为一个词向量模型，作者还跟BERT比训练成本以突出自己的优势，着实是让人尴尬了一把，由此也可见作者为了讲这个故事的“煞费苦心”了。

BioHash #

BioHash出自论文《Bio-Inspired Hashing for Unsupervised Similarity Search》，它是一种将向量二值化的方法，跟传统的的LSH不一样的是，它依赖于样本，是为特定数据集“量身定制”的，因此通常能得到效果更好、更稀疏的二值向量。

给定向量集$\{\boldsymbol{x}_i\}_{i=1}^N$，BioHash算法大致如下：

1、用K-Means将$\{\boldsymbol{x}_i\}_{i=1}^N$聚为$K$类，得到$K$个向量中心；

2、每个$\boldsymbol{x}_i$映射为一个$K$维0/1向量，其中与$\boldsymbol{x}_i$距离最近的$k$个类对应的位置为1，其余为0。

之所以说“大致”，是因为算法细节上有一些出入。首先，聚类过程中用的距离不是欧式距离，而是归一化内积，即$d(\boldsymbol{x}, \boldsymbol{w}) = -\langle \boldsymbol{x}, \boldsymbol{w} / \Vert\boldsymbol{w}\Vert\rangle$，这个做法我们之前在探究Capsule的时候也用过，读者可以参考《再来一顿贺岁宴：从K-Means到Capsule》；然后，求解聚类中心的时候，用的是SGD而不是常规的EM算法，这一点其实笔者不大理解，虽说SGD可以小批量进行，对内存更友好，但理论上EM算法也可以按批执行，不至于爆内存；最后，笔者完全不理解的一点是，在聚类过程中作者用的距离是归一化内积$-\langle \boldsymbol{x}, \boldsymbol{w} / \Vert\boldsymbol{w}\Vert\rangle$，但在决定每个样本的归属的时候，又以不归一化的内积$-\langle \boldsymbol{x}, \boldsymbol{w}\rangle$为距离，实在是莫名其妙。

当然，抛开BioHash的细节不说，BioHash的效果还是很赞的，所以有适当的场景的话，BioHash还是值得借鉴使用的。细心的读者可能会发现，BioWord和BioHash有几位作者是相同的，事实上它们都产自同一个实验室，由此也不难理解BioWord希望传承BioHash的初衷，只不过将BioHash用于词向量构建中，笔者认为无论从动机上还是论文所报告的效果上，都难以称得上漂亮。

FlyHash #

说了那么久，我们还没有说到标题的问题：BioWord到底跟果蝇有什么联系？或者说BioHash的哪个地方体现了跟果蝇的相似性？追踪BioHash的参考文献可以发现，BioHash事实上是对一个名为FlyHash的算法的改进，因此要溯源的话，还得找FlyHash。

顾名思义，FlyHash主要是受到果蝇的嗅觉回路启发而构思出来的一种新的向量二值化方法，它相比常规的LSH更高效。对于不了解LSH的读者来说，我们后面再补充介绍一下，这里先直接介绍FlyHash。其实FlyHash跟LSH都是“随机投影 + 二值化”的思路，只不过果蝇启发了一个新的优化方向：高维 + 低激活。

具体来说，设原始数据$\boldsymbol{x}_i \in \mathbb{R}^{D}$，FlyHash选择了一个随机二值矩阵$\boldsymbol{W}\in\{0,1\}^{D\times K}$（选好后就固定了），其中一般有$K > D$（高维），经过投影后$\boldsymbol{x}_i \boldsymbol{W}$是一个$K$维向量，然后对它进行一个WTA（Winner Take All，赢者通吃）操作来实现”低激活“——“将$\boldsymbol{x}_i \boldsymbol{W}$最大的$k$个元素置1，其余置0”，这样就得到了一个有$k$个1、$K-k$个0的二值向量了，就将它作为$\boldsymbol{x}_i$的Hash向量。

由于激活值只有有限的$k$个，因此就算升维了，存储和检索成本都不会加大，反而效果有所提升，这就是果蝇带来的“高维 + 低激活”思路的好处。FlyHash首先发表在Science的论文《A neural algorithm for a fundamental computing problem》，关于“高维 + 低激活”的果蝇嗅觉回路可以仔细参考这篇论文，后来论文《Improving Similarity Search with High-dimensional Locality-sensitive Hashing》又进一步完善了理论部分，这两篇论文也是一脉相承的。

所以，现在我们可以回答“怎么跟果蝇搭上关系”了，其实就是在二值化过程中包含了“高维 + 低激活”思想的算法，我们都可以说“Inspired by Fly”，由于FlyHash是随机投影来得到最终结果的，所以它必须升到足够多维才能保证效果，而BioHash针对具体数据集进行训练，因此它往往不需要FlyHash那么多维，而且效果还更好，但BioHash也有明显的“赢者通吃”的思想，所以也称“Inspired by Fly”。而BioWord使用了BioHash，因此也自称“Inspired by Fly”了。

LSH #

最后，我们简单介绍一下LSH（Locality Sensitive Hashing），供不了解的读者参考。完整的LSH讲起来又可以长篇大论了，这里主要提一下跟FlyHash比较密切的部分。

简单来说，LSH就是一个将向量二值化的算法，并且二值化之后的向量能近似保持度量不变。常见的一种方案是通过随机投影来（近似）保持cos值的不变性，从之前的文章《n维空间下两个随机向量的夹角分布》和《从几何视角来理解模型参数的初始化策略》我们可以知道，高维空间中任意两个高斯随机向量几乎都是正交的，那么从$\mathcal{N}(0,1/n)$中采样$DK$个随机数来组成一个矩阵$\boldsymbol{W}\in\mathbb{R}^{D\times K}$，它“几乎”是一个正交矩阵。这样一来，两个原始向量$\boldsymbol{x}_i, \boldsymbol{x}_j\in\mathbb{R}^{D}$被$\boldsymbol{W}$一乘后，就变成了两个$K$维向量，并且夹角近似不变：
\begin{equation}\cos(\boldsymbol{x}_i \boldsymbol{W}, \boldsymbol{x}_j \boldsymbol{W})\approx \cos(\boldsymbol{x}_i, \boldsymbol{x}_j)\end{equation}
这样一来，如果检索度量是cos值，那么我们可以用投影后的$\boldsymbol{x} \boldsymbol{W}$代替原始向量$\boldsymbol{x}$来做近似检索。更进一步，将结果二值化后基本也能保持cos值不变：
\begin{equation}\boldsymbol{x}\quad\to\quad\text{sgn}(\boldsymbol{x} \boldsymbol{W})\end{equation}
其中$\text{sgn}$是符号函数，将大于0的改为1，小于等于0的改为-1，这样就将原始向量映射为一个二值向量了。这里的目标维度$K$一般不会比$D$大，并且由于投影的随机性，我们大约可以认为结果之中1和-1都是各一半，这就跟FlyHash的“高维 + 低激活”有明显区别了，因为不管你将1还是将-1视为激活值，数目都差不多，称不上“低激活”。

上面的介绍虽然只是一个启发性的引导，但事实上背后是有严格的概率理论支撑的（在《Performer：用随机投影将Attention的复杂度线性化》也做过相关的理论分析），因此LSH是一套严谨的可量化的算法，并不是纯粹拍脑袋的近似。对向量二值化之后，我们就可以将它视为一个词袋模型（哪怕原来的是连续型向量），进而可以对它建立索引来加速检索，比如倒排索引，这就是向量二值化的意义了，像Fiass等向量检索库，都包含了LSH算法。

文章小结 #

本文对一个二值化词向量模型进行了溯源，探究了它究竟是如何联系上果蝇的，从中我们还可以了解到BioHash、FlyHash、LSH等向量二值化方法的思路和关联。本文也是第一次尝试倒叙式写作，希望读者喜欢～

转载到请包括本文地址：https://kexue.fm/archives/8159

更详细的转载事宜请参考：《科学空间FAQ》