Nyströmformer：基于矩阵分解的线性化Attention方案

标准Attention的$\mathcal{O}(n^2)$复杂度可真是让研究人员头大。前段时间我们在博文《Performer：用随机投影将Attention的复杂度线性化》中介绍了Google的Performer模型，它通过随机投影的方式将标准Attention转化为线性Attention。无独有偶，前些天Arxiv上放出了AAAI 2021的一篇论文《Nyströmformer: A Nyström-Based Algorithm for Approximating Self-Attention》，里边又提出了一种从另一个角度把标准Attention线性化的方案。

该方案写的是Nyström-Based，顾名思义是利用了Nyström方法来近似标准Attention的。但是坦白说，在看到这篇论文之前，笔者也完全没听说过Nyström方法，而纵观整篇论文，里边也全是笔者一眼看上去感觉很茫然的矩阵分解推导，理解起来颇为困难。不过有趣的是，尽管作者的推导很复杂，但笔者发现最终的结果可以通过一个相对来说更简明的方式来理解，遂将笔者对Nyströmformer的理解整理在此，供大家参考。

简单的回顾 #

如果读者对线性Attention还不是很了解，那么建议先通读一下《线性Attention的探索：Attention必须有个Softmax吗？》和《Performer：用随机投影将Attention的复杂度线性化》。总的来说，线性Attention是通过矩阵乘法的结合律来降低Attention的复杂度。

标准Attention #

标准的Scaled-Dot Attention写成矩阵形式就是（有时候指数部分还会多个缩放因子，这里我们就不显式写出来了）：
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\boldsymbol{Q}\boldsymbol{K}^{\top}\right)\boldsymbol{V}\end{equation}
这里$\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}\in\mathbb{R}^{n\times d}$（对应Self Attention）。此外，本文的所有softmax，都是对矩阵的第二个维度做归一化。

在上式中，$\boldsymbol{Q}\boldsymbol{K}^{\top}$这一步必须要先算出来，然后才能算softmax，它导致了我们不能使用矩阵乘法的结合律。而$\boldsymbol{Q}\boldsymbol{K}^{\top}$是$n^2$个向量的内积，因此时间和空间复杂度都是$\mathcal{O}(n^2)$。

线性Attention #

而线性Attention比较朴素的做法就是
\begin{equation}\left(\phi(\boldsymbol{Q})\varphi(\boldsymbol{K})^{\top}\right)\boldsymbol{V}=\phi(\boldsymbol{Q})\left(\varphi(\boldsymbol{K})^{\top}\boldsymbol{V}\right)\end{equation}
其中$\phi,\varphi$是值域非负的激活函数。为了方便对比，上式还没有显式地写出归一化因子，只突出了主要计算量的部分。上式左端的复杂度依然是$\mathcal{O}(n^2)$的，由于矩阵乘法满足结合律，我们可以先算后面两个矩阵的乘法，这样整体复杂度就降为$\mathcal{O}(n)$了。

上式是直接将Attention定义为两个矩阵的乘法来利用乘法结合律的，也可以将标准Attention（近似地）转化为矩阵的乘法来利用结合律，如下一节提到的Performer；此外，相乘矩阵也不一定是两个，比如本文要介绍的Nyströmformer就是将注意力表示为三个矩阵相乘的。

Performer #

对于Performer来说，它是通过随机投影来找到矩阵$\tilde{\boldsymbol{Q}},\tilde{\boldsymbol{K}}\in\mathbb{R}^{n\times m}$使得softmax中的$e^{\boldsymbol{Q}\boldsymbol{K}^{\top}}\approx \tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}$，这样一来标准Attention就可以近似为上一节的线性Attention来算了，细节请看之前的博文《Performer：用随机投影将Attention的复杂度线性化》。

如果对SVM和核方法等比较熟悉的读者可能会联想到，这个做法其实就是核函数的思想，即低维空间中两个向量的核函数可以映射为高维空间中两个向量的内积。它也可以跟LSH（Locality Sensitive Hashing）联系起来。

Nyströmformer #

在这部分内容中，我们以一个简单的双重softmax形式的线性Attention为出发点，逐步寻找更加接近标准Attention的线性Attention，从而得到Nyströmformer。

Nyströmformer结构示意图。读者可以读完下面几节后再来对照着理解这个图。

双重Softmax #

在文章《线性Attention的探索：Attention必须有个Softmax吗？》中我们提到了一种比较有意思的线性Attention，它使用了双重softmax来构建Attention矩阵：
\begin{equation}\left(softmax(\boldsymbol{Q}) softmax\left(\boldsymbol{K}^{\top}\right)\right)\boldsymbol{V}=softmax(\boldsymbol{Q})\left(softmax\left(\boldsymbol{K}^{\top}\right)\boldsymbol{V}\right)\label{eq:2sm}\end{equation}
可以证明这样构造出来的Attention矩阵自动满足归一化要求，不得不说这是一种简单漂亮的线性Attention方案。

不过，直接对$\boldsymbol{Q},\boldsymbol{K}^{\top}$做softmax似乎有点奇怪，总感觉没有经过相似度（内积）对比就直接softmax会有哪里不对劲。为了解决这个问题，Nyströmformer先分别将$\boldsymbol{Q},\boldsymbol{K}$视为$n$个$d$维向量，然后聚成$m$类来得到$m$个聚类中心构成的矩阵$\tilde{\boldsymbol{Q}},\tilde{\boldsymbol{K}}\in\mathbb{R}^{m\times d}$，这时候我们可以通过下述公式来定义Attention：
\begin{equation}\left(softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}} ^{\top}\right)softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\right)\boldsymbol{V} = softmax\left(\boldsymbol{Q} \tilde{\boldsymbol{K}}^{\top}\right)\left(softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\boldsymbol{V}\right)\label{eq:2sm2}\end{equation}
具体的聚类过程我们稍后再来讨论。现在，softmax的对象是内积的结果，具有比较鲜明的物理意义，因此可以认为上式比前面的式$\eqref{eq:2sm}$更为合理。如果我们选定一个比较小的$m$，那么上式右端的复杂度只是线性地依赖于$n$，因此它也是一个线性Attention。

向标准靠近 #

纯粹从改进式$\eqref{eq:2sm}$的角度来看，式$\eqref{eq:2sm2}$已经达到目标了，不过Nyströmformer并不局限于此，它还希望改进后的结果与标准Attention更加接近。为此，观察到式$\eqref{eq:2sm2}$的注意力矩阵$softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}}^{\top}\right)softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)$是一个$n\times m$的矩阵乘以一个$m\times n$的矩阵，为了微调结果，又不至于增加过多的复杂度，我们可以考虑在中间插入一个$m\times m$的矩阵$\boldsymbol{M}$：
\begin{equation}softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}} ^{\top}\right) \,\boldsymbol{M}\, softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\end{equation}
如何选择$\boldsymbol{M}$呢？一个合理的要求是当$m=n$时应当完全等价于标准Attention，此时$\tilde{\boldsymbol{Q}}=\boldsymbol{Q}, \tilde{\boldsymbol{K}}=\boldsymbol{K}$，推出
\begin{equation}\boldsymbol{M} = \left(softmax\left(\boldsymbol{Q}\boldsymbol{K}^{\top}\right)\right)^{-1} = \left(softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)\right)^{-1}\end{equation}
对于一般的$m$，$\left(softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)\right)^{-1}$恰好是一个$m\times m$矩阵，因此选它作为$\boldsymbol{M}$至少在矩阵运算上是合理的，而根据$m=n$时的特殊情况我们则“大胆地”推测选它作为$\boldsymbol{M}$能让新的Attention机制更接近标准Attention，因此Nyströmformer最终选择的是
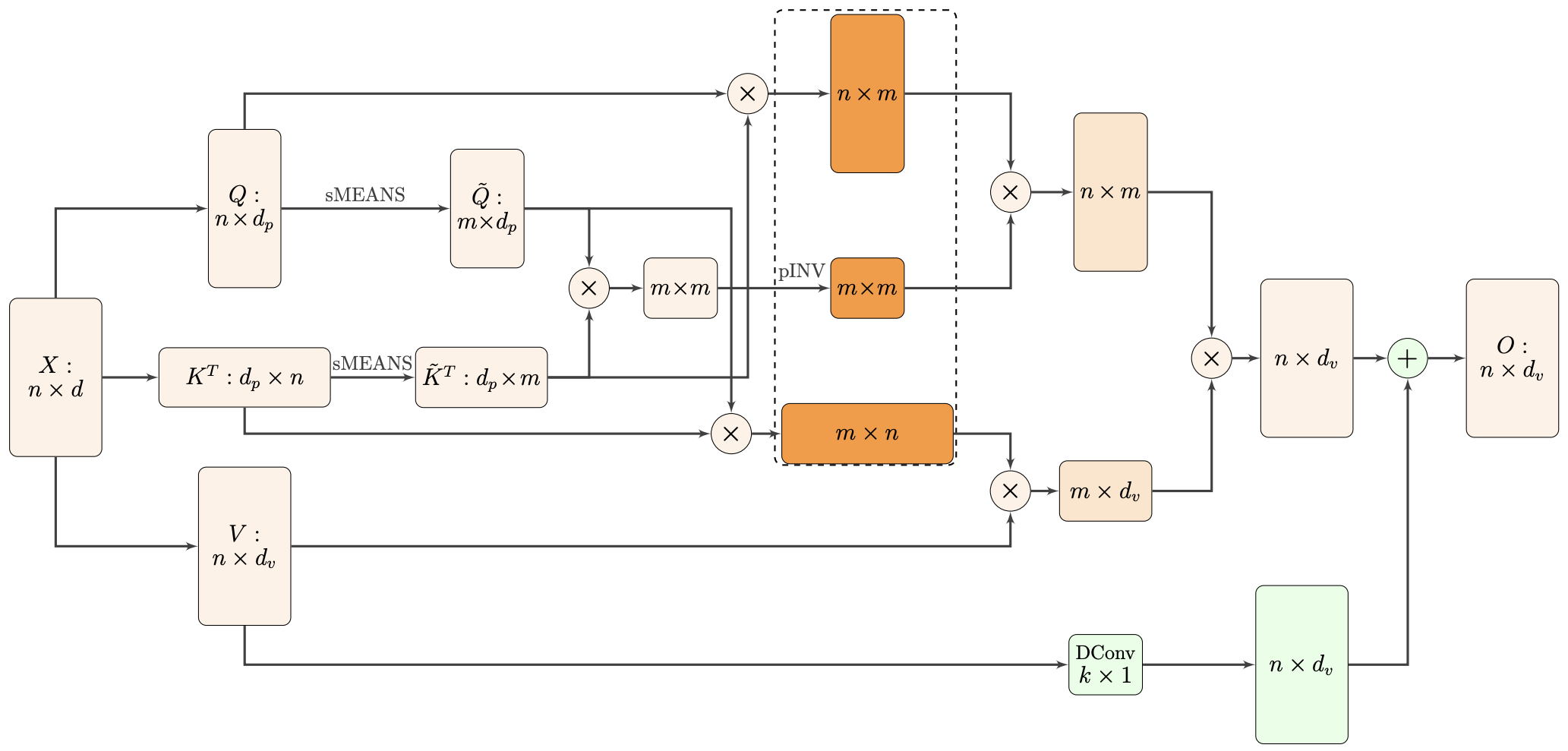
\begin{equation}softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}} ^{\top}\right) \, \left(softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)\right)^{-1} \, softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\end{equation}
作为Attention矩阵，它是三个小矩阵的乘积，因此通过矩阵乘法的结合律就能转化为线性Attention。

不过，还有一个理论上的小细节需要补充一下，那就是上式涉及到矩阵的求逆，而$softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)$未必是可逆的。当然，从实践上来看，一个实数的方阵不可逆的概率几乎为零（不可逆意味着行列式严格等于0，从概率上来看不等于0自然比等于0的概率大得多），因此这种情况在具体实验中可以不考虑，但理论上还是得完善的。这个其实也简单，如果是不可逆的矩阵，那就换成“伪逆”就好（记号为$^{\dagger}$），它对任意矩阵都存在，并且当矩阵可逆时伪逆跟逆相等。

因此，最终的Nyströmformer的Attention矩阵形式为
\begin{equation}softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}} ^{\top}\right) \, \left(softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)\right)^{\dagger} \, softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\label{eq:2sm3}\end{equation}

迭代求逆阵 #

从理论上看，式$\eqref{eq:2sm3}$已经达到目标了，不过落实到实践上还需要处理好一些细节问题，比如上述伪逆怎么求。伪逆又叫广义逆、Moore-Penrose逆等，标准的求法是通过SVD来求，设矩阵$\boldsymbol{A}$的SVD分解为$\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{V}^{\top}$，那么它的伪逆为
\begin{equation}\boldsymbol{A}^{\dagger} = \boldsymbol{V} \boldsymbol{\Lambda}^{\dagger} \boldsymbol{U}^{\top}\end{equation}
其中对角阵$\boldsymbol{\Lambda}$的伪逆$\boldsymbol{\Lambda}^{\dagger}$等于将它对角线所有非零值取倒数所得到的新对角阵。SVD的求法虽然理论上比较简单易懂，但计算量还是比较大的，而且也不容易求梯度，因此并不是实现伪逆的理想方式。

Nyströmformer采用了迭代求逆的近似方法。具体来说，它采用了论文《Chebyshev-type methods and preconditioning techniques》提供的迭代算法：

若初始矩阵$\boldsymbol{V}_0$满足$\Vert \boldsymbol{I} - \boldsymbol{A} \boldsymbol{V}_0\Vert < 1$，那么对于下述迭代格式 \begin{equation}\begin{aligned} \boldsymbol{V}_{n+1} =&\,\left[\boldsymbol{I} + \frac{1}{4}\left(\boldsymbol{I} - \boldsymbol{V}_n \boldsymbol{A}\right)\left(3 \boldsymbol{I} - \boldsymbol{V}_n \boldsymbol{A}\right)^2\right] \boldsymbol{V}_n \\ =&\,\frac{1}{4} \boldsymbol{V}_n (13 \boldsymbol{I} − \boldsymbol{A} \boldsymbol{V}_n (15 \boldsymbol{I} − \boldsymbol{A} \boldsymbol{V}_n (7 \boldsymbol{I} − \boldsymbol{A} \boldsymbol{V}_n))) \end{aligned}\end{equation} 成立$\lim\limits_{n\to\infty} \boldsymbol{V}_n = \boldsymbol{A}^{\dagger}$。

这里的$\Vert\cdot\Vert$可以是任意一种矩阵范数，满足条件的一个比较简单的初始值可以是
\begin{equation}\boldsymbol{V}_0 = \frac{\boldsymbol{A}^{\top}}{\Vert\boldsymbol{A}\Vert_1 \Vert\boldsymbol{A}\Vert_{\infty}} = \frac{\boldsymbol{A}^{\top}}{\left(\max\limits_j\sum\limits_i |A_{i,j}|\right)\left(\max\limits_i\sum\limits_j |A_{i,j}|\right)}\end{equation}
在Nyströmformer论文中，作者直接用上述初始值和迭代格式进行迭代，将迭代6次的结果来代替$\boldsymbol{A}^{\dagger}$。迭代6次看上去很多，但事实上论文所选取的$m$比较小（论文写的是64），迭代过程中又只涉及到矩阵乘法，因此迭代计算量不会太大，而且只有乘法的话求梯度就很轻松了。这样求伪逆的问题就算是解决了，论文将这个迭代过程简写为pINV。

池化当聚类 #

还需要解决的另一个问题是聚类方法的选择，比较直接的想法自然就是直接套用K-Means了。然而，同前面求伪逆所面临的问题一样，在设计模型时不仅要考虑前向计算，还需要考虑反向传播的求梯度，直接套用K-Means涉及到$\mathop{\text{argmin}}$操作，无法求出有意义的梯度，需要将它“软化”才能嵌入到模型中，这一系列操作下来，其实就相当于胶囊网络的“动态路由”过程，细节我们在《再来一顿贺岁宴：从K-Means到Capsule》讨论过。这个方案的主要问题是K-Means是一个迭代过程，需要迭代几次才能保证效果，这导致计算量明显加大，不是特别理想。

Nyströmformer选了一个非常简单的方案：假设序列长度$n$是$m$的整数倍（如果不是，padding零向量），那么将$\boldsymbol{Q},\boldsymbol{K}$的每$n/m$个向量求平均作为$\tilde{\boldsymbol{Q}}, \tilde{\boldsymbol{K}}$的每个向量。这个操作叫做Adaptive Average Pooling（原论文称为Segment-Means，简称sMEANS），即是一种平均池化方法，通过自适应窗口大小使得平均池化后的特征矩阵具有固定的形状。Nyströmformer的实验表明，不需要比较复杂的聚类方法，就这样使用简单的自适应池化就可以取得非常有竞争力的效果了，而且只需要选择$m=64$，跟映射前的$d$是一般大小，这比Performer要选择比$d$大几倍的$m$要好得多了。

不过，自适应池化的一个明显缺点是会“糅合”每一个区间的信息，导致它不能防止未来信息泄漏而不能做自回归生成（语言模型或者Seq2Seq的解码器），这基本是任何带有Pooling技术的模型的缺点。

实验与分析 #

这里我们汇总一下Nyströmformer的实验结果，并且分享一下笔者对它的一些看法和思考。

性能与效果 #

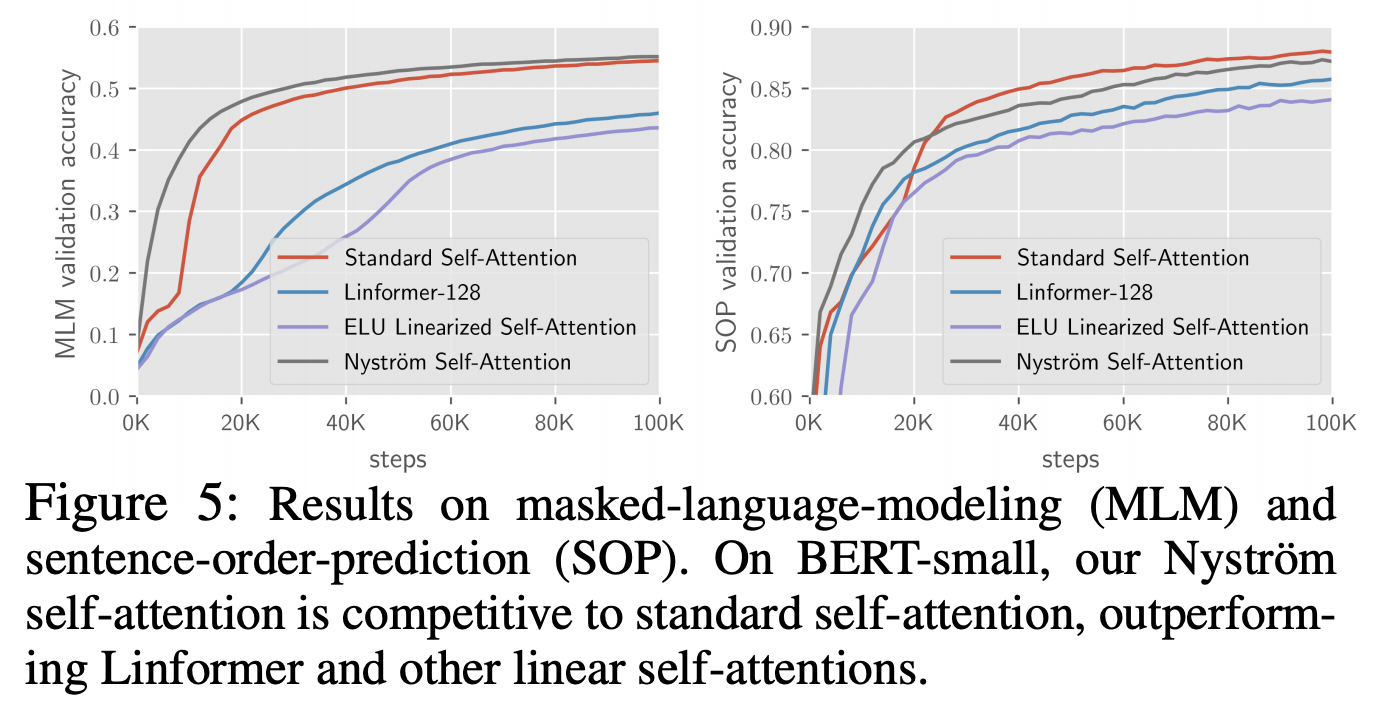
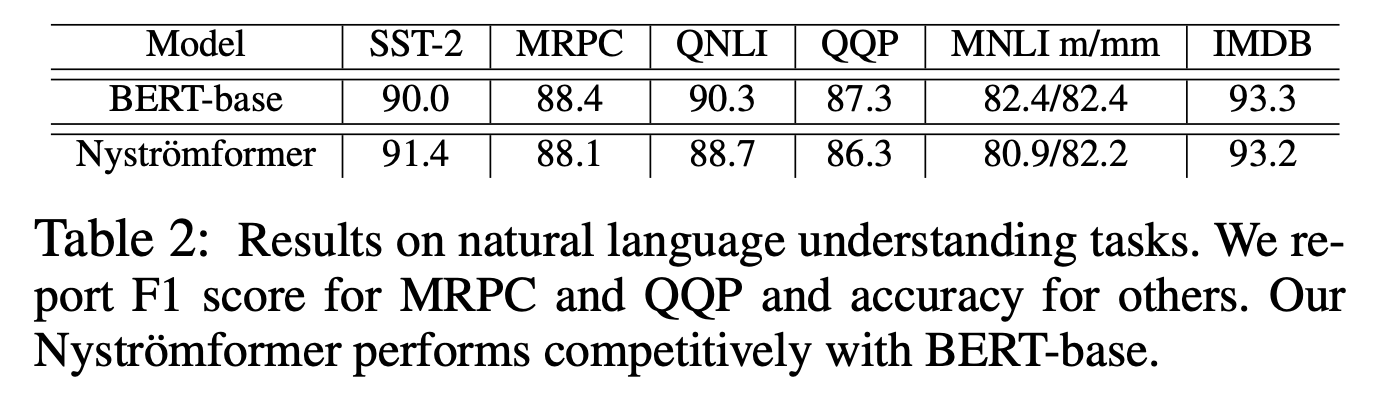
可能受限于算力，原论文做的实验不算特别丰富，主要是将small和base版本的BERT里边的标准Attention替换为Nyströmformer进行对比实验，实验结果主要是下面两个图。其中一个是预训练效果图，其中比较有意思的是Nyströmformer在MLM任务上的效果比标准Attention还要优；另外是在下游任务上的微调效果，显示出跟标准Attention（即BERT）比还是有竞争力的。

Nyströmformer在预训练任务（MLM和SOP）上的效果

Nyströmformer在下游任务的微调效果

不过，原论文并没有比较Nyströmformer跟同类模型的效果差异，只是提供下面的一张复杂度对比图，因此无法更好地突出Nyströmformer的竞争力：

不同模型的时间和空间复杂度对比图

个人的思考 #

总的来说，Nyströmformer对标准Attention进行近似线性化的思路还是比较新颖的，值得学习与参考。不过伪逆部分的处理总感觉有点不大自然，这部分可能是未来的一个改进点，如果可以做到不用近似，那就比较完美了。还有，如何定量地估计Nyströmformer与标准Attention的误差，也是一个值得思考的理论问题。

从实验上来看，Nyströmformer跟标准Attention相比还是显得有竞争力的，尤其是MLM的结果比标准Attention还好，显示了Nyströmformer的潜力。此外，前面说到包含了Pooling导致不能做自回归生成是Nyströmformer的一个显著缺点，不知道有没有办法可以弥补，反正笔者目前是没有想到好的方向。

跟Performer相比，Nyströmformer去除了线性化过程中的随机性，因为Performer是通过随机投影来达到线性化的，这必然会带来随机性，对于某些有强迫症的读者来说，这个随机性可能是难以接受的存在，而Nyströmformer则不存在这种随机性，因此也算是一个亮点。

Nyström方法 #

可能有些读者还是想学习一下Nyström方法，这里稍微补充一下。要理解Nyström方法，需要先简单认识一下矩阵的CUR分解。

大家可能都听说过矩阵的SVD分解，格式为$\boldsymbol{A}=\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{V}^{\top}$，其中$\boldsymbol{U},\boldsymbol{V}$是正交矩阵而$\boldsymbol{\Lambda}$是对角矩阵。要注意$\boldsymbol{U},\boldsymbol{V}$是正交矩阵意味着它们是稠密的，那么当$\boldsymbol{A}$很大的时候SVD的计算成本和储存成本都很大（哪怕是做了近似）。现在假设$\boldsymbol{A}$很大但很稀疏，那么它的SVD分解比原始矩阵还不划算得多得多。为此，CUR分解应运而生，它希望从原矩阵中选择$k$列组成矩阵$\boldsymbol{C}$、选择$k$行组成矩阵$\boldsymbol{R}$，并插入一个$k\times k$的矩阵$\boldsymbol{U}$，使得
\begin{equation}\boldsymbol{A} \approx \boldsymbol{C}\boldsymbol{U}\boldsymbol{R}\end{equation}
由于$\boldsymbol{C},\boldsymbol{R}$都是原句子的一部分，因此也继承了稀疏性。关于CUR分解，读者还可以参考斯坦福的CS246课程的《Dimensionality Reduction》一节。跟SVD不同的是，CUR分解在笔者看来更多的是一种分解思想而不是具体的分解算法，它有不同的实现方式，比如Nyström方法也算是其中一种，分解形式为
\begin{equation}\begin{pmatrix}\boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{D}\end{pmatrix} \approx \begin{pmatrix}\boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{C}\boldsymbol{A}^{\dagger}\boldsymbol{B}\end{pmatrix} = \begin{pmatrix}\boldsymbol{A} \\ \boldsymbol{C}\end{pmatrix} \boldsymbol{A}^{\dagger} \begin{pmatrix}\boldsymbol{A} & \boldsymbol{B}\end{pmatrix}\end{equation}
其中$\begin{pmatrix}\boldsymbol{A} \\ \boldsymbol{C}\end{pmatrix}$和$\begin{pmatrix}\boldsymbol{A} & \boldsymbol{B}\end{pmatrix}$选出来的列矩阵和行矩阵，这里为了方便描述，假设了经过排列后选出来的行列均排在矩阵前面。Nyströmformer其实也没有直接用Nyström方法（事实上也直接套用不了，原论文有描述），而是借鉴了Nyström方法的分解思想而已。

关于Nyström方法，原论文主要引用的是《Improving CUR Matrix Decomposition and the Nyström Approximation via Adaptive Sampling》，但并不推荐新手读这篇论文，而推荐读《Matrix Compression using the Nystro ̈m Method》和《Using the Nyström Method to Speed Up Kernel Machines》。

要特别说明的是，对于CUR分解和Nyström方法，笔者也是新学的，可能有理解不当的地方，请读者自行甄别理解，也欢迎熟悉相关理论的读者交流指正。

来一个小结 #

本文介绍了提升Transformer效率的一个新工作Nyströmformer，它借鉴了Nyström方法的思想来构建一个能逼近标准Attention的线性Attention，类似思想的工作还有Performer，两者相比各有自己的优缺点，都是值得学习的工作。本文分享了笔者自己对Nyströmformer的理解，窃认为这种途径更加易懂一些，如有谬误，肯请读者指正。

转载到请包括本文地址：https://kexue.fm/archives/8180

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。