科学空间|Scientific Spaces

在之前的文章《最小熵原理（六）：词向量的维度应该怎么选择？》中，我们基于最小熵思想推导出了一个词向量维度公式“$n > 8.33\log N$”，然后在《让人惊叹的Johnson-Lindenstrauss引理：应用篇》中我们进一步指出，该结果与JL引理所给出的$\mathcal{O}(\log N)$是吻合的。

既然理论上看上去很完美，那么自然就有读者发问了：实验结果如何呢？8.33这个系数是最优的吗？本文就对此问题的相关内容做一个简单汇总。

词向量

首先，我们可以直接，当$N$为10万时，$8.33\log N\approx 96$，当$N$为500万时，$8.33\log N\approx 128$。这说明，至少在数量级上，该公式给出的结果是很符合我们实际所用维度的，因为在词向量时代，我们自行训练的词向量维度也就是100维左右。可能有读者会质疑，目前开源的词向量多数是300维的，像BERT的Embedding层都达到了768维，这不是明显偏离了你的结果了？

点击阅读全文...

随着NLP的发展，像Word2Vec、Glove这样的词向量模型，正逐渐地被基于Transformer的BERT等模型代替，不过经典始终是经典，词向量模型依然在不少场景发光发热，并且仍有不少值得我们去研究的地方。本文我们来关心一个词向量模型可能有的疑惑：词向量的维度大概多少才够？

先说结论，笔者给出的估算结果是
\begin{equation}n > 8.33\log N\label{eq:final}\end{equation}
更简约的话可以直接记$n > 8\log N$，其中$N$是词表大小，$n$就是词向量维度，$\log$是自然对数。当$n$超过这个阈值时，就说明模型有足够的容量容纳这$N$个词语（当然$n$越大过拟合风险也越大）。这样一来，当$N=100000$时，得到的$n$大约是96，所以对于10万个词的词向量模型来说，维度选择96就足够了；如果要容纳500万个词，那么$n$大概就是128。

点击阅读全文...

生成模型一直是笔者比较关注的主题，不管是NLP和CV的生成模型都是如此。这篇文章里，我们介绍一个新颖的生成模型，来自论文《Batch norm with entropic regularization turns deterministic autoencoders into generative models》，论文中称之为EAE（Entropic AutoEncoder）。它要做的事情给变分自编码器（VAE）基本一致，最终效果其实也差不多（略优），说它新颖并不是它生成效果有多好，而是思路上的新奇，颇有别致感。此外，借着这个机会，我们还将学习一种统计量的估计方法——$k$邻近方法，这是一种很有用的非参数估计方法。

自编码器vs生成模型

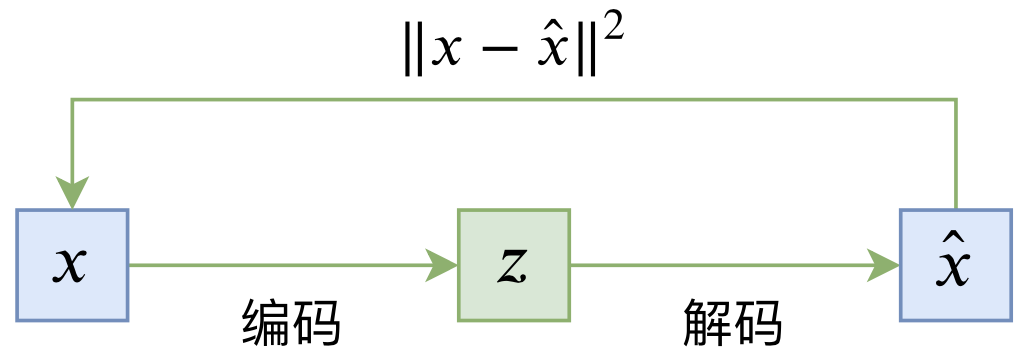
普通的自编码器是一个“编码-解码”的重构过程，如下图所示：

典型自编码器示意图

其loss一般为
\begin{equation}L_{AE} = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - \hat{x}\right\Vert^2\right] = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - D(E(x))\right\Vert^2\right]\end{equation}

点击阅读全文...

让我们不厌其烦地回顾一下：最小熵原理是一个无监督学习的原理，“熵”就是学习成本，而降低学习成本是我们的不懈追求，所以通过“最小化学习成本”就能够无监督地学习出很多符合我们认知的结果，这就是最小熵原理的基本理念。

这篇文章里，我们会介绍一种相当漂亮的聚类算法，它同样也体现了最小熵原理，或者说它可以通过最小熵原理导出来，名为InfoMap，或者MapEquation。事实上InfoMap已经是2007年的成果了，最早的论文是《Maps of random walks on complex networks reveal community structure》，虽然看起来很旧，但我认为它仍是当前最漂亮的聚类算法，因为它不仅告诉了我们“怎么聚类”，更重要的是给了我们一个“为什么要聚类”的优雅的信息论解释，并从这个解释中直接导出了整个聚类过程。

一个复杂有向图网络示意图。图片来自InfoMap最早的论文《Maps of random walks on complex networks reveal community structure》

当然，它的定位并不仅仅局限在聚类上，更准确地说，它是一种图网络上的“社区发现”算法。所谓社区发现（Community Detection），大概意思是给定一个有向/无向图网络，然后找出这个网络上的“抱团”情况，至于详细含义，大家可以自行搜索一下。简单来说，它跟聚类相似，但是比聚类的含义更丰富。（还可以参考《什么是社区发现?》）

点击阅读全文...

从第一篇看下来到这里，我们知道所谓“最小熵原理”就是致力于降低学习成本，试图用最小的成本完成同样的事情。所以整个系列就是一个“偷懒攻略”。那偷懒的秘诀是什么呢？答案是“套路”，所以本系列又称为“套路宝典”。

本篇我们介绍图书馆里边的套路。

先抛出一个问题：词向量出现在什么时候？是2013年Mikolov的Word2Vec？还是是2003年Bengio大神的神经语言模型？都不是，其实词向量可以追溯到千年以前，在那古老的图书馆中...

图书馆一角（图片来源于百度搜索）

走进图书馆

图书馆里有词向量？还是千年以前？在哪本书？我去借来看看。

放书的套路

其实不是哪本书，而是放书的套路。

很明显，图书馆中书的摆放是有“套路”的：它们不是随机摆放的，而是分门别类地放置的，比如数学类放一个区，文学类放一个区，计算机类也放一个区；同一个类也有很多子类，比如数学类中，数学分析放一个子区，代数放一个子区，几何放一个子区，等等。读者是否思考过，为什么要这么分类放置？分类放置有什么好处？跟最小熵又有什么关系？

点击阅读全文...

在前一文《最小熵原理（二）：“当机立断”之词库构建》中，我们以最小熵原理为出发点进行了一系列的数学推导，最终得到$(2.15)$和$(2.17)$式，它告诉我们两个互信息比较大的元素我们应该将它们合并起来，这有利于降低“学习难度”。于是利用这一原理，我们通过邻字互信息来实现了词库的无监督生成。

由字到词、由词到词组，考察的是相邻的元素能不能合并成一个好“套路”。可是套路为什么非得要相邻的呢？当然不一定相邻，我们学习语言的时候，不仅仅会学习到词语、词组，还要学习到“固定搭配”，也就是说词语怎么运用才是合理的，这是语法的体现，是本文所要探究的，希望最终能达到一定的无监督句法分析的效果。

由于这次我们考虑的是跨邻词的语言关联，因此我给它起个名字为“飞象过河”，正是

“套路宝典”第二式——“飞象过河”

语言结构

对于大多数人来说，并不会真正知道什么是语法，他们脑海里就只有一些“固定搭配”、“定式”，或者更正式一点可以叫“模版”。大多数情况下，我们是根据模版来说出合理的话来。而不同的人的说话模版可能有所不同，这就是个人的说话风格，甚至是“口头禅”。

点击阅读全文...

在本文，我们介绍“套路宝典”第一式——“当机立断”：1、导出平均字信息熵的概念，然后基于最小熵原理推导出互信息公式；2、并且完成词库的无监督构建、给出一元分词模型的信息熵诠释，从而展示有关生成套路、识别套路的基本方法和技巧。

这既是最小熵原理的第一个使用案例，也是整个“套路宝典”的总纲。

你练或者不练，套路就在那里，不增不减。

为什么需要词语

从上一篇文章可以看到，假设我们根本不懂中文，那么我们一开始会将中文看成是一系列“字”随机组合的字符串，但是慢慢地我们会发现上下文是有联系的，它并不是“字”的随机组合，它应该是“套路”的随机组合。于是为了减轻我们的记忆成本，我们会去挖掘一些语言的“套路”。第一个“套路”，是相邻的字之间的组合定式，这些组合定式，也就是我们理解的“词”。

平均字信息熵

假如有一批语料，我们将它分好词，以词作为中文的单位，那么每个词的信息量是$-\log p_w$，因此我们就可以计算记忆这批语料所要花费的时间为
$$-\sum_{w\in \text{语料}}\log p_w\tag{2.1}$$
这里$w\in \text{语料}$是对语料逐词求和，不用去重。如果不分词，按照字来理解，那么需要的时间为
$$-\sum_{c\in \text{语料}}\log p_c\tag{2.2}$$

点击阅读全文...

话在开头

在深度学习等端到端方案已经逐步席卷NLP的今天，你是否还愿意去思考自然语言背后的基本原理？我们常说“文本挖掘”，你真的感受到了“挖掘”的味道了吗？

无意中的邂逅

前段时间看了一篇关于无监督句法分析的文章，继而从它的参考文献中发现了论文《Redundancy Reduction as a Strategy for Unsupervised Learning》，这篇论文介绍了如何从去掉空格的英文文章中将英文单词复原。对应到中文，这不就是词库构建吗？于是饶有兴致地细读了一番，发现论文思路清晰、理论完整、结果漂亮，让人赏心悦目。

尽管现在看来，这篇论文的价值不是很大，甚至其结果可能已经被很多人学习过了，但是要注意：这是一篇1993年的论文！在PC机还没有流行的年代，就做出了如此前瞻性的研究。虽然如今深度学习流行，NLP任务越做越复杂，这确实是一大进步，但是我们对NLP原理的真正了解，还不一定超过几十年前的前辈们多少。

这篇论文是通过“去冗余”（Redundancy Reduction）来实现无监督地构建词库的，从信息论的角度来看，“去冗余”就是信息熵的最小化。无监督句法分析那篇文章也指出“信息熵最小化是无监督的NLP的唯一可行的方案”。我进而学习了一些相关资料，并且结合自己的理解思考了一番，发现这个评论确实是耐人寻味。我觉得，不仅仅是NLP，信息熵最小化很可能是所有无监督学习的根本。

点击阅读全文...