科学空间|Scientific Spaces

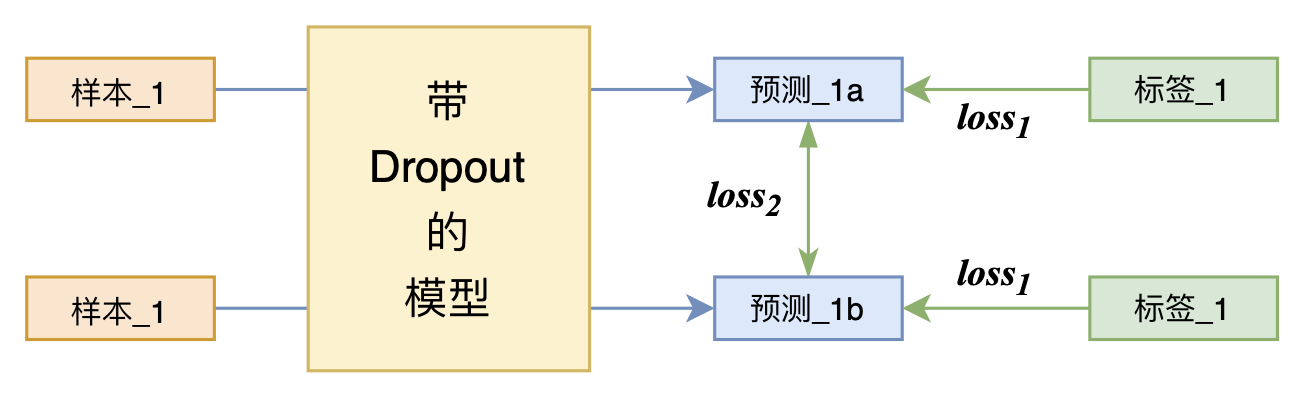
关注NLP新进展的读者，想必对四月份发布的SimCSE印象颇深，它通过简单的“Dropout两次”来构造正样本进行对比学习，达到了无监督语义相似度任务的全面SOTA。无独有偶，最近的论文《R-Drop: Regularized Dropout for Neural Networks》提出了R-Drop，它将“Dropout两次”的思想用到了有监督任务中，每个实验结果几乎都取得了明显的提升。此外，笔者在自己的实验还发现，它在半监督任务上也能有不俗的表现。

R-Drop示意图

小小的“Dropout两次”，居然跑出了“五项全能”的感觉，不得不令人惊讶。本文来介绍一下R-Drop，并分享一下笔者对它背后原理的思考。

点击阅读全文...

类别不平衡问题，也称为长尾分布问题，在本博客里已经有好几次相关讨论了，比如《从loss的硬截断、软化到focal loss》、《将“Softmax+交叉熵”推广到多标签分类问题》、《通过互信息思想来缓解类别不平衡问题》。对于缓解类别不平衡，比较基本的方法就是调节样本权重，看起来“高端”一点的方法则是各种魔改loss了（比如Focal Loss、Dice Loss、Logits Adjustment等），本文希望比较系统地理解一下它们之间的联系。

长尾分布：少数类别的样本数目非常多，多数类别的样本数目非常少。

从光滑准确率到交叉熵

这里的分析主要以sigmoid的2分类为主，但多数结论可以平行推广到softmax的多分类。设$x$为输入，$y\in\{0,1\}$为目标，$p_{\theta}(x) \in [0, 1]$为模型。理想情况下，当然是要评测什么指标，我们就去优化那个指标。对于分类问题来说，最朴素的指标当然就是准确率，但准确率并没有办法提供有效的梯度，所以不能直接来训练。

点击阅读全文...

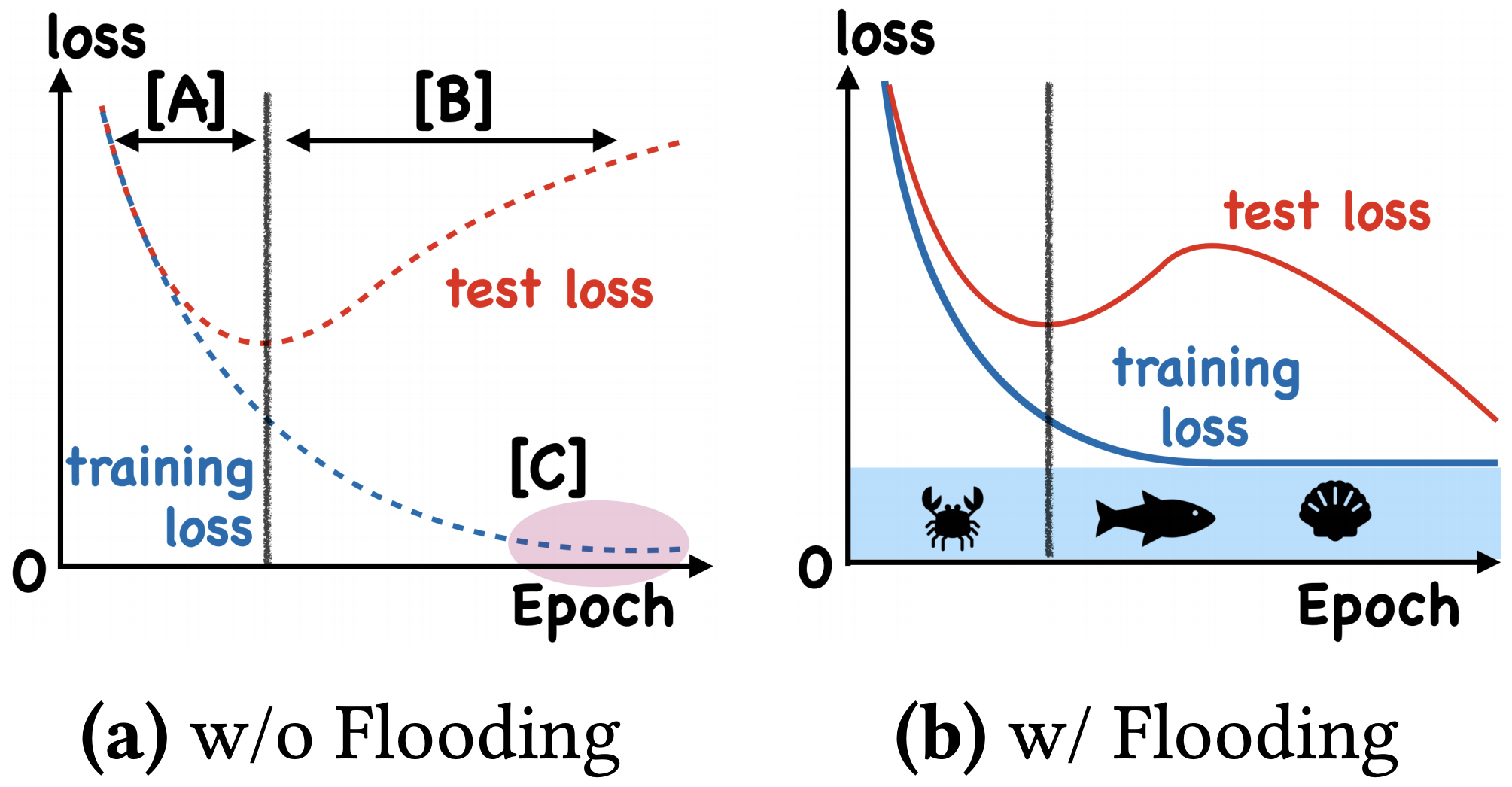
在训练模型的时候，我们需要损失函数一直训练到0吗？显然不用。一般来说，我们是用训练集来训练模型，但希望的是验证集的损失越小越好，而正常来说训练集的损失降低到一定值后，验证集的损失就会开始上升，因此没必要把训练集的损失降低到0。

既然如此，在已经达到了某个阈值之后，我们可不可以做点别的事情来提升模型性能呢？ICML 2020的论文《Do We Need Zero Training Loss After Achieving Zero Training Error?》回答了这个问题。不过论文的回答也仅局限在“是什么”这个层面上，并没很好地描述“为什么”，另外看了知乎上kid丶大佬的解读，也没找到自己想要的答案。因此自己分析了一下，记录在此。

左图：不加Flooding的训练示意图；右图：加了Flooding的训练示意图

点击阅读全文...

类别不平衡问题，也叫“长尾问题”，是机器学习面临的常见问题之一，尤其是来源于真实场景下的数据集，几乎都是类别不平衡的。大概在两年前，笔者也思考过这个问题，当时正好对“互信息”相关的内容颇有心得，所以构思了一种基于互信息思想的解决办法，但又想了一下，那思路似乎过于平凡，所以就没有深究。然而，前几天在arxiv上刷到Google的一篇文章《Long-tail learning via logit adjustment》，意外地发现里边包含了跟笔者当初的构思几乎一样的方法，这才意识到当初放弃的思路原来还能达到SOTA的水平～于是结合这篇论文，将笔者当初的构思过程整理于此，希望不会被读者嫌弃“马后炮”。

问题描述

这里主要关心的是单标签的多分类问题，假设有$1,2,\cdots,K$共$K$个候选类别，训练数据为$(x,y)\sim\mathcal{D}$，建模的分布为$p_{\theta}(y|x)$，那么我们的优化目标是最大似然，或者说最小化交叉熵，即
\begin{equation}\mathop{\text{argmin}}_{\theta}\,\mathbb{E}_{(x,y)\sim\mathcal{D}}[-\log p_{\theta}(y|x)]\end{equation}

点击阅读全文...

（注：本文的相关内容已整理成论文《ZLPR: A Novel Loss for Multi-label Classification》，如需引用可以直接引用英文论文，谢谢。）

一般来说，在处理常规的多分类问题时，我们会在模型的最后用一个全连接层输出每个类的分数，然后用softmax激活并用交叉熵作为损失函数。在这篇文章里，我们尝试将“Softmax+交叉熵”方案推广到多标签分类场景，希望能得到用于多标签分类任务的、不需要特别调整类权重和阈值的loss。

类别不平衡

单标签到多标签

一般来说，多分类问题指的就是单标签分类问题，即从$n$个候选类别中选$1$个目标类别。假设各个类的得分分别为$s_1,s_2,
\dots,s_n$，目标类为$t\in\{1,2,\dots,n\}$，那么所用的loss为
\begin{equation}-\log \frac{e^{s_t}}{\sum\limits_{i=1}^n e^{s_i}}= - s_t + \log \sum\limits_{i=1}^n e^{s_i}\label{eq:log-softmax}\end{equation}
这个loss的优化方向是让目标类的得分$s_t$变为$s_1,s_2,\dots,s_t$中的最大值。关于softmax的相关内容，还可以参考《寻求一个光滑的最大值函数》、《函数光滑化杂谈：不可导函数的可导逼近》等文章。

点击阅读全文...

继续“让Keras更酷一些！”系列，让Keras来得更有趣些吧～

这次围绕着Keras的loss、metric、权重和进度条进行展开。

可以不要输出

一般我们用Keras定义一个模型，是这样子的：

x_in = Input(shape=(784,))
x = x_in
x = Dense(100, activation='relu')(x)
x = Dense(10, activation='softmax')(x)

model = Model(x_in, x)
model.compile(loss='categorical_crossentropy ',
              optimizer='adam',
              metrics=['accuracy'])
model.fit(x_train, y_train, epochs=5)

点击阅读全文...

Keras伴我走来

回想起进入机器学习领域的这两三年来，Keras是一直陪伴在笔者的身边。要不是当初刚掉进这个坑时碰到了Keras这个这么易用的框架，能快速实现我的想法，我也不确定我是否能有毅力坚持下来，毕竟当初是theano、pylearn、caffe、torch等的天下，哪怕在今天它们对我来说仍然像天书一般。

后来为了拓展视野，我也去学习了一段时间的tensorflow，用纯tensorflow写过若干程序，但不管怎样，仍然无法割舍Keras。随着对Keras的了解的深入，尤其是花了一点时间研究过Keras的源码后，我发现Keras并没有大家诟病的那样“欠缺灵活性”。事实上，Keras那精巧的封装，可以让我们轻松实现很多复杂的功能。我越来越感觉，Keras像是一件非常精美的艺术品，充分体现了Keras的开发者们深厚的创作功力。

本文介绍Keras中自定义模型的一些内容，相对而言，这属于Keras进阶的内容，刚入门的朋友请暂时忽略。

层的自定义

这里介绍Keras中自定义层及其一些运用技巧，在这之中我们可以看到Keras层的精巧之处。

点击阅读全文...

搞计算机视觉的朋友会知道，AM-Softmax是人脸识别中的成果。所以这篇文章就是借鉴人脸识别的做法来做句子相似度模型，顺便介绍在Keras下各种margin loss的写法。

背景

细想之下会发现，句子相似度与人脸识别有很多的相似之处～

已有的做法

在我搜索到的资料中，深度学习做句子相似度模型，就只有两种做法：一是输入一对句子，然后输出一个0/1标签代表相似程度，也就是视为一个二分类问题，比如《Learning Text Similarity with Siamese Recurrent Networks》中的模型是这样的

将句子相似度视为二分类模型

包括今年拍拍贷的“魔镜杯”，也是这种格式。另外一种做法是输入一个三元组“（句子A，跟A相似的句子，跟A不相似的句子）”，然后用triplet loss的做法解决，比如文章《Applying Deep Learning To Answer Selection: A Study And An Open Task》中的做法。

这两种做法其实也可以看成是一种，本质上是一样的，只不过loss和训练方法有所差别。但是，这两种方法却都有一个很严重的问题：负样本采样严重不足，导致效果提升非常慢。

点击阅读全文...