“闭门造车”之多模态思路浅谈(三):位置编码
By 苏剑林 | 2024-09-06 | 65609位读者 | 引用在前面的文章中,我们曾表达过这样的观点:多模态LLM相比纯文本LLM的主要差异在于,前者甚至还没有形成一个公认为标准的方法论。这里的方法论,不仅包括之前讨论的生成和训练策略,还包括一些基础架构的设计,比如本文要谈的“多模态位置编码”。
对于这个主题,我们之前在《Transformer升级之路:17、多模态位置编码的简单思考》就已经讨论过一遍,并且提出了一个方案(RoPE-Tie)。然而,当时笔者对这个问题的思考仅处于起步阶段,存在细节考虑不周全、认识不够到位等问题,所以站在现在的角度回看,当时所提的方案与完美答案还有明显的距离。
因此,本文我们将自上而下地再次梳理这个问题,并且给出一个自认为更加理想的结果。
多模位置
多模态模型居然连位置编码都没有形成共识,这一点可能会让很多读者意外,但事实上确实如此。对于文本LLM,目前主流的位置编码是RoPE(RoPE就不展开介绍了,假设读者已经熟知),更准确来说是RoPE-1D,因为原始设计只适用于1D序列。后来我们推导了RoPE-2D,这可以用于图像等2D序列,按照RoPE-2D的思路我们可以平行地推广到RoPE-3D,用于视频等3D序列。
当Batch Size增大时,学习率该如何随之变化?
By 苏剑林 | 2024-11-14 | 41470位读者 | 引用随着算力的飞速进步,有越多越多的场景希望能够实现“算力换时间”,即通过堆砌算力来缩短模型训练时间。理想情况下,我们希望投入$n$倍的算力,那么达到同样效果的时间则缩短为$1/n$,此时总的算力成本是一致的。这个“希望”看上去很合理和自然,但实际上并不平凡,即便我们不考虑通信之类的瓶颈,当算力超过一定规模或者模型小于一定规模时,增加算力往往只能增大Batch Size。然而,增大Batch Size一定可以缩短训练时间并保持效果不变吗?
这就是接下来我们要讨论的话题:当Batch Size增大时,各种超参数尤其是学习率该如何调整,才能保持原本的训练效果并最大化训练效率?我们也可以称之为Batch Size与学习率之间的Scaling Law。
方差视角
直觉上,当Batch Size增大时,每个Batch的梯度将会更准,所以步子就可以迈大一点,也就是增大学习率,以求更快达到终点,缩短训练时间,这一点大体上都能想到。问题就是,增大多少才是最合适的呢?
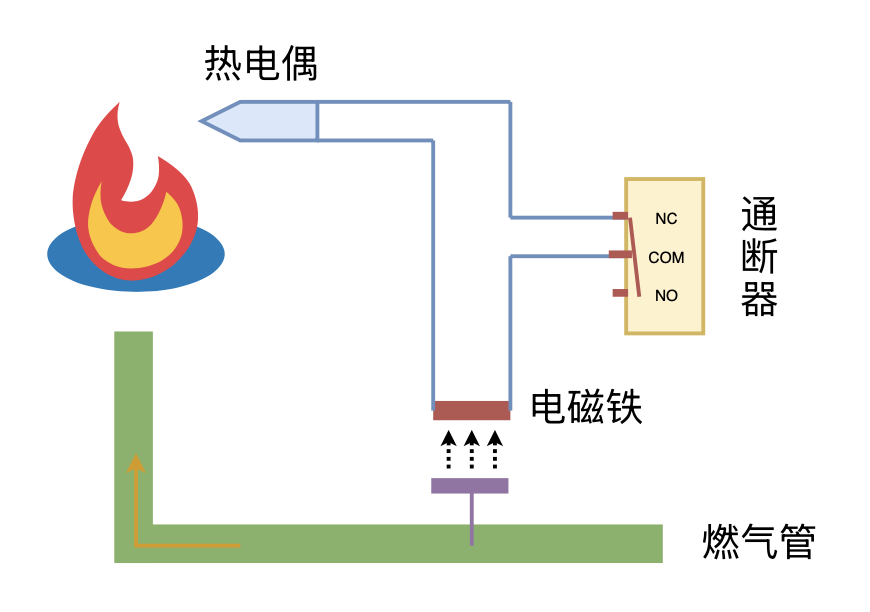
利用“熄火保护 + 通断器”实现燃气灶智能关火
By 苏剑林 | 2024-09-26 | 19722位读者 | 引用低秩近似之路(三):CR
By 苏剑林 | 2024-10-11 | 22795位读者 | 引用在《低秩近似之路(二):SVD》中,我们证明了SVD可以给出任意矩阵的最优低秩近似。那里的最优近似是无约束的,也就是说SVD给出的结果只管误差上的最小,不在乎矩阵的具体结构,而在很多应用场景中,出于可解释性或者非线性处理等需求,我们往往希望得到具有某些特殊结构的近似分解。
因此,从这篇文章开始,我们将探究一些具有特定结构的低秩近似,而本文将聚焦于其中的CR近似(Column-Row Approximation),它提供了加速矩阵乘法运算的一种简单方案。
问题背景
矩阵的最优$r$秩近似的一般提法是
\begin{equation}\mathop{\text{argmin}}_{\text{rank}(\tilde{\boldsymbol{M}})\leq r}\Vert \tilde{\boldsymbol{M}} - \boldsymbol{M}\Vert_F^2\label{eq:loss-m2}\end{equation}
低秩近似之路(四):ID
By 苏剑林 | 2024-10-30 | 23227位读者 | 引用这篇文章的主角是ID(Interpolative Decomposition),中文可以称之为“插值分解”,它同样可以理解为是一种具有特定结构的低秩分解,其中的一侧是该矩阵的若干列(当然如果你偏好于行,那么选择行也没什么问题),换句话说,ID试图从一个矩阵中找出若干关键列作为“骨架”(通常也称作“草图”)来逼近原始矩阵。
可能很多读者都未曾听说过ID,即便维基百科也只有几句语焉不详的介绍(链接),但事实上,ID跟SVD一样早已内置在SciPy之中(参考scipy.linalg.interpolative),这侧面印证了ID的实用价值。
基本定义
前三篇文章我们分别介绍了伪逆、SVD、CR近似,它们都可以视为寻找特定结构的低秩近似:
\begin{equation}\mathop{\text{argmin}}_{\text{rank}(\tilde{\boldsymbol{M}})\leq r}\Vert \tilde{\boldsymbol{M}} - \boldsymbol{M}\Vert_F^2\end{equation}
让MathJax的数学公式随窗口大小自动缩放
By 苏剑林 | 2024-10-15 | 18146位读者 | 引用随着MathJax的出现和流行,在网页上显示数学公式便逐渐有了标准答案。然而,MathJax(包括其竞品KaTeX)只是负责将网页LaTeX代码转化为数学公式,对于自适应分辨率方面依然没有太好的办法。像本站一些数学文章,因为是在PC端排版好的,所以在PC端浏览效果尚可,但转到手机上看就可能有点难以入目了。
经过测试,笔者得到了一个方案,让MathJax的数学公式也能像图片一样,随着窗口大小而自适应缩放,从而尽量保证移动端的显示效果,在此跟大家分享一波。
背景思路
这个问题的起源是,即便在PC端进行排版,有时候也会遇到一些单行公式的长度超出了网页宽度,但又不大好换行的情况,这时候一个解决方案是用HTML代码手动调整一下公式的字体大小,比如
<span style="font-size:90%">
\begin{equation}一个超长的数学公式\end{equation}
</span>VQ的旋转技巧:梯度直通估计的一般推广
By 苏剑林 | 2024-10-24 | 30491位读者 | 引用随着多模态LLM的方兴未艾,VQ(Vector Quantization)的地位也“水涨船高”,它可以作为视觉乃至任意模态的Tokenizer,将多模态数据统一到自回归生成框架中。遗憾的是,自VQ-VAE首次提出VQ以来,其理论并没有显著进步,像编码表的坍缩或利用率低等问题至今仍亟待解决,取而代之的是FSQ等替代方案被提出,成为了VQ有力的“竞争对手”。
然而,FSQ并不能在任何场景下都替代VQ,所以VQ本身的改进依然是有价值的。近日笔者读到了《Restructuring Vector Quantization with the Rotation Trick》,它提出了一种旋转技巧,声称能改善VQ的一系列问题,本文就让我们一起来品鉴一下。
回顾
早在五年前的博文《VQ-VAE的简明介绍:量子化自编码器》中我们就介绍过了VQ-VAE,后来在《简单得令人尴尬的FSQ:“四舍五入”超越了VQ-VAE》介绍FSQ的时候,也再次仔细地温习了VQ-VAE,还不了解的读者可以先阅读这两篇文章。
细水长flow之TARFLOW:流模型满血归来?
By 苏剑林 | 2025-01-17 | 28152位读者 | 引用不知道还有没有读者对这个系列有印象?这个系列取名“细水长flow”,主要介绍flow模型的相关工作,起因是当年(2018年)OpenAI发布了一个新的流模型Glow,在以GAN为主流的当时来说着实让人惊艳了一番。但惊艳归惊艳,事实上在相当长的时间内,Glow及后期的一些改进在生成效果方面都是比不上GAN的,更不用说现在主流的扩散模型了。
不过局面可能要改变了,上个月的论文《Normalizing Flows are Capable Generative Models》提出了新的流模型TARFLOW,它在几乎在所有的生成任务效果上都逼近了当前SOTA,可谓是流模型的“满血”回归。









最近评论