未来的天地枢纽——太空天梯
By 苏剑林 | 2010-10-22 | 25060位读者 | 引用漫话
BoJone认为,科学的意义并非在于无休止地计算,而是利用有限的科学理论来解释尽可能多的自然、生活现象。正因如此,科学家们追求和谐、简洁、优美的科学理论。科学就是想方设法地把未知变成已知,并在此基础上进一步发展。
随着媒体技术的发展,我们接触信息的渠道越来越多。每每我们从互联网或报纸上看到一则科学新闻时,我们几乎都会为之兴奋。但是,外行看热闹,内行看门道。对于真正热爱科学的朋友来说,也许会更加感兴趣新闻内容的来由。也就是说,我们希望进一步了解结论是怎样得出来的——哪怕只是在很浅的层面上认识。
意犹未尽——继续光学曲线
By 苏剑林 | 2010-11-13 | 55116位读者 | 引用《自然极值》系列——1.前言
By 苏剑林 | 2010-11-27 | 54766位读者 | 引用附:期中考过后,课程紧了,自由时间少了,因此科学空间的更新也放缓了。不过BoJone也会尽量地更新一些内容,和大家一同分享学习的乐趣。
上一周和这一周的时间里,BoJone将自己学习物理和极值的一些内容进行了总结和整合,写成了《自然极值》一文。因此从今天起,到十二月的大多数时间里,科学空间将和大家讲述并讨论关于“极值”的问题,希望读者会喜欢这部分内容。当然,我不是专业的研究人员,更不是经验丰富的物理和数学教师,甚至可以说是一个“乳臭未干的小子”,因此,错误在所难免,只希望同好不吝指出,更希冀能够起到我抛出的这一块“砖”能够引出美妙的“玉”。
今天上体育课的时候,BoJone与同学们正兴致勃勃地打着篮球,不料临近下课之时,同学猛一击(当然只是无意摩擦,没有恶意),我感到一阵猛疼——眼角处的肉破裂了!开始的一分钟内不停流血,奇怪的是到了校医室之后血就止住了(还没有经过任何处理,只是一直按住)。本以为只是小伤,简单处理就好,谁知校医说需要到外边的医院缝针,否则可能留疤毁容!!
既然如此严重,无奈只能服从了,简单处理伤口后就和母亲一起到了医院,缝了两针。由于接下来两天都得去医院消毒清洗伤口,所以干脆就请假回家了,周一再上学吧(貌似我在学校也仅仅是自学,没有多大区别^_^)...不过从受伤到现在,我还没有机会看到我的伤口究竟咋样...
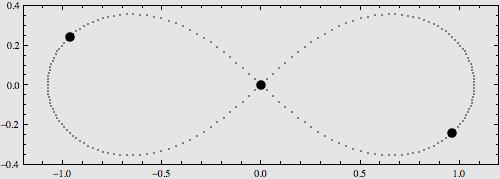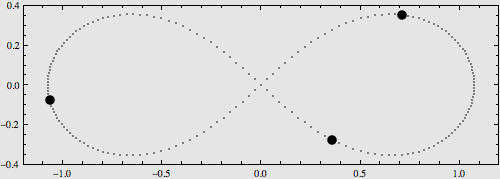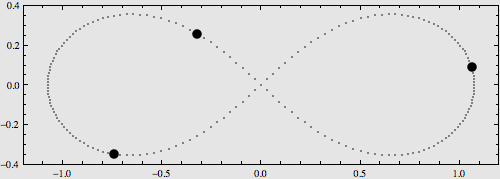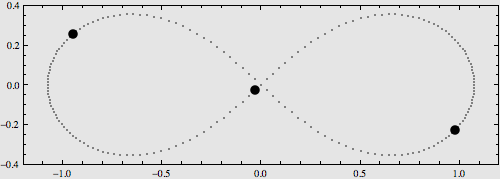
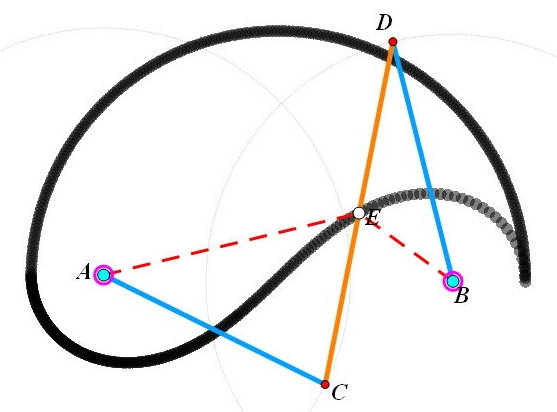
N体问题的30个周期性解
By 苏剑林 | 2010-12-19 | 58333位读者 | 引用《自然极值》系列——8.极值分析
By 苏剑林 | 2010-12-26 | 49038位读者 | 引用本篇文章是《自然极值》系列最后一篇文章,估计也是2010年最后一篇文章了。在这个美好的2010年,想必大家一定收获匪浅,BoJone也在2010年成长了很多。在2010年的尾声,BoJone和科学空间都祝大家在新的一年里更加开心快乐,在科学的道路上更快速地前行。
在本文,BoJone将与大家讨论求极值的最基本原理。这一探讨思路受到了天才的费恩曼所著《费恩曼物理讲义》的启迪。我们分别对函数求极值(求导)和泛函数极值(变分)进行一些简略的分析。
一、函数求极值
对于一个函数$y=f(x)$,设想它在$x=x_0$处取到最大值,那么显然对于很小的增量$\Delta x$,有
$$f(x_0+\Delta x) \leq f(x_0)\tag{3}$$根据泰勒级数,我们有
$f(x_0+\Delta x)=f(x_0)+f'(x_0)\Delta x$————(4)
[遐想]细胞的进化是一次次“大吞并”?
By 苏剑林 | 2011-11-06 | 44837位读者 | 引用传说中的高三备考是一次全面系统的大复习,但对于我们而言,它并不是复习,而是学习。我发现很多知识点在以前都是鲜有接触的,这无疑说明了两个问题:当时我学习得很肤浅;我的遗忘力太强了。就拿生物来说吧,以前总是很简单地就跳阅过去了,从不会去思考一些深入的问题。现在的重新“复习”阶段,却饶有兴趣地引出了很多的思考。特别是有关细胞进化的讨论,显得特别有趣。
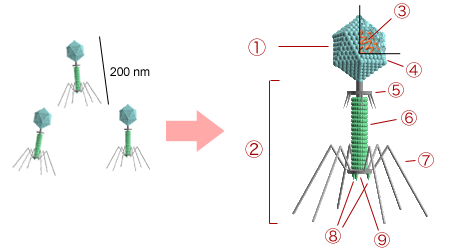
根据古生物的研究,地球上第一个生命起源于32亿年前,是一个很简单的原核细胞,其遗传物质是RNA,后来逐渐演变成以DNA为遗传物质,例如细菌有一个环状的DNA分子。原核生物很快就进化出了真核生物,因为迄今所知最古老的真核生物化石已有近21亿年的历史,许多科学家推测,最早的真核生物可能早在30亿年前就出现了。
这里便引申出了一个问题:病毒是什么时候出现的?它是怎么出现的?








![闭区间[a,b]上的连续函数?(x),其最大值为红色点,最小值为蓝色点](/usr/uploads/2010/11/3941873990.png)


最近评论