30
Jan
【NASA每日一图】Messier 88
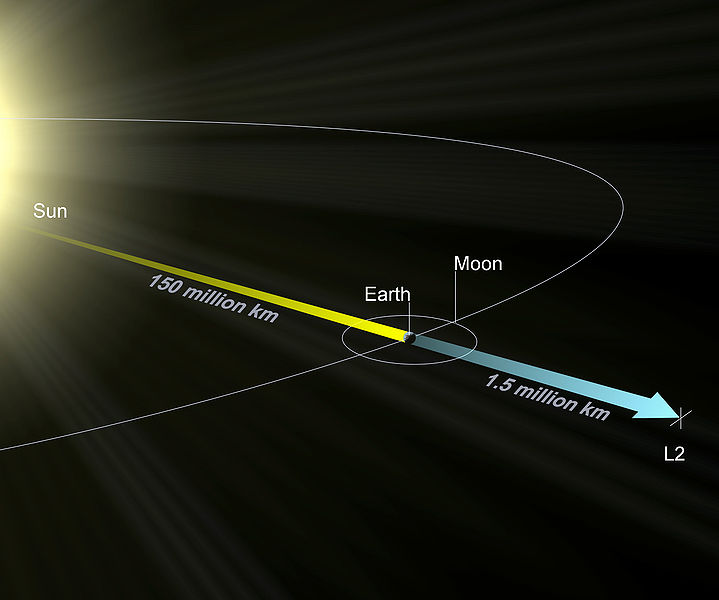
By 苏剑林 | 2010-01-30 | 19971位读者 | 引用
15
Aug
《方程与宇宙》:拉格朗日点的点点滴滴(四)
By 苏剑林 | 2010-08-15 | 91464位读者 | 引用The New Calculation Of Lagrangian Point 1,2,3
L2_rendering
关于n体问题，选择质心或其他定点为参考点，我们可以列出下面的运动方程：
$$\ddot{\vec{r}}_k=\sum_{i=1,i != k}^{n} Gm_i\frac{\vec{r}_i-\vec{r}_k}{|\vec{r}_i-\vec{r}_k|^3}\tag{19}$$
现在我们只考虑三体问题。天文学家一直希望能够找到三体问题的简洁解，可是很遗憾，庞加莱已经证明了三体问题的解是混沌的，也就是说任何微小的扰动都有可能造成不可预料的后果（可以形象的比喻为：巴西的一只蝴蝶翅膀的扇动，有可能因此美国的一场龙卷风）。
23
Aug
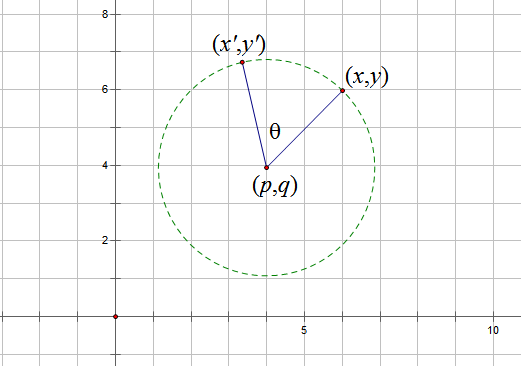
《向量》系列——4.天旋地转(向量,复数,极坐标)
By 苏剑林 | 2010-08-23 | 39126位读者 | 引用
26
Jan
唠叨下，关于三体问题周期轨道
By 苏剑林 | 2011-01-26 | 32541位读者 | 引用
15
May
地球引力场的悬链线方程
By 苏剑林 | 2011-05-15 | 60314位读者 | 引用之前曾在《自然极值》系列文章中提到过均匀重力场下的悬链线形状问题，并且在那文章中向读者提出：在一个质点（地球）引力场中的悬链线形状会是怎么样的。说实话，提出这个问题的时候，我还不懂怎么解答这个问题，不过现在会了，回头一看，已经几个月了，时间过得真快...
与之前的思路一样，我们依旧采用的是“平衡态公理”，即总势能最小。从天体力学中我们知道，任意两个质点间的势能为$-\frac{Gm_1 m_2}{r}$。对于本题的悬链线问题，我们可以把地球放到坐标原点位置，而悬链的两个固定点分别为$(x_1,y_1)$和$(x_2,y_2)$，链的总长度为l。即
$$\int_{x_1}^{x_2} \sqrt{dx^2+dy^2}=l$$
学着《还珠格格3之天上人间》中的情节，今天我也把自己书架上的书搬上楼去晒晒。
有的书是新买的，有的已经买了一两年了，不管怎样，都拿上去沐浴阳光。
后来才发现，把书搬上去很累很热，把书搬下来重新整理更累更热。整个过程从早上九点开始，直到下午两点才完全结束。
原来，把书搬到太阳下展开的场景很壮观......
当然，晒书只是一个契机，我顺便收拾了一下凌乱的房间，这次算是比较彻底了，一些平常没有清洁的角落都清理了一遍。因为再过几天就正式成为高三了。也许下一次晒书，或者下一次整理，已经是明年的今天了。所以不论怎样，今天都要好好“干一场”！
书籍是人类进步的阶梯，呵呵^_^
八月一号开始我们这里的高三就正式开学了，以后每周都只能在星期天中午到下午的一小段时间里跟读者们见见面了^_^
高三的生活的确很枯燥、烦闷，特别是老师那句重复了无数遍的话“这个知识点在高考是这样出题的...”让我感觉十分讨厌，难道，学习就为了高考？就算真的是难以改变的现状，我也偏不服从。高考是要准备的，“活”也是要“生”的，为了生活而生存，而不是为了生存而生活。
虽然很忙，但我还是会抽一些时间出来研究自己感兴趣的东西的，如研究一下几何、不等式、多项式、对称等等，还有发一下呆^_^，当然也尽可能抽一些时间来这里写写我的学习心得吧——当然，频率应该会很低。
我相信，一年之后我不会后悔的。
2
Aug
复分析学习1：揭示微分与积分的联系
By 苏剑林 | 2012-08-02 | 34425位读者 | 引用笔者这段时间对复数尤其感兴趣，当然，严格来讲应该是复变函数内容，其中一个原因是通过它，我们可以把一些看似毫不相关的内容联系了起来，体现了数学的简洁美和统一美。我相当有兴趣的其中一个内容是实分析中的泰勒级数和傅里叶级数。这两者都是关于某个函数的级数展开式，其中泰勒级数是用于一般函数展开的，其各项系数通过求n阶导数得到；傅里叶级数的对象是周期函数，其各项系数是通过定积分求得的。在实数世界里，两者毫不相关，但是，复分析却告诉我们：它们只是同一个东西！只是将其在不同的角度“投影”到实数世界里，就产生了不同的“物像”，以至于我们认为它们是不同东西而已。
我们直接来看一个变魔术般的运算：
我们知道，在实数世界里头，我们有
$ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+...$，其中$|x| < 1$
最近评论