之前曾在《自然极值》系列文章中提到过均匀重力场下的悬链线形状问题，并且在那文章中向读者提出：在一个质点（地球）引力场中的悬链线形状会是怎么样的。说实话，提出这个问题的时候，我还不懂怎么解答这个问题，不过现在会了，回头一看，已经几个月了，时间过得真快...

与之前的思路一样，我们依旧采用的是“平衡态公理”，即总势能最小。从天体力学中我们知道，任意两个质点间的势能为$-\frac{Gm_1 m_2}{r}$。对于本题的悬链线问题，我们可以把地球放到坐标原点位置，而悬链的两个固定点分别为$(x_1,y_1)$和$(x_2,y_2)$，链的总长度为l。即
$$\int_{x_1}^{x_2} \sqrt{dx^2+dy^2}=l$$

设悬链的线密度为1（无量纲处理，长度即质量）。那么悬链上的点(x,y)到(x+dx,y+dy)一小段的引力势能可以记为
$$dE=-GM\frac{\sqrt{dx^2+dy^2}}{\sqrt{x^2+y^2}}$$

总势能显然是$$E=-GM\int_{x_1}^{x_2} \frac{\sqrt{dx^2+dy^2}}{\sqrt{x^2+y^2}}$$

选取适当的坐标对被积函数进行化简是很必要的，我们采取极坐标系：
$$\frac{\sqrt{dx^2+dy^2}}{\sqrt{x^2+y^2}}=\frac{\sqrt{r^2 d\theta^2+dr^2}}{r}=\frac{\sqrt{r^2 \dot{\theta}^2+1}}{r}dr$$

其中$\dot{\theta}=\frac{d\theta}{dr}$

于是$$E=-GM\int_{r_1}^{r_2} \frac{\sqrt{r^2 \dot{\theta}^2+1}}{r}dr=-GM\int_{r_1}^{r_2} F(\dot{\theta},r)dr$$

代入拉格朗日方程就得到（将r看成自变量，θ作为函数）：
$$0=\frac{\partial F }{\partial \theta}=\frac{d}{dr}(\frac{\partial F }{\partial \dot{\theta}})=\frac{d}{dr}(\frac{r\dot{\theta}}{\sqrt{r^2 \dot{\theta}^2+1}})$$

于是积分得到$\frac{r\dot{\theta}}{\sqrt{r^2 \dot{\theta}^2+1}}=Const$

并且化简得到：$$r^2 \dot{\theta}^2=C_1^2 ( C_1 > 0 )$$

要求$C_1 > 0 $只是为了描述上的方便，即$\pm \dot{\theta}=\frac{C_1}{r} \Rightarrow C_2 \pm \theta=C_1 ln r$

我们约定，在$\theta=C_1 ln r-C_2 < 0$时，上面去负号，反之取正号，则可以写成：
$$C_2 + |\theta|=C_1 ln r$$

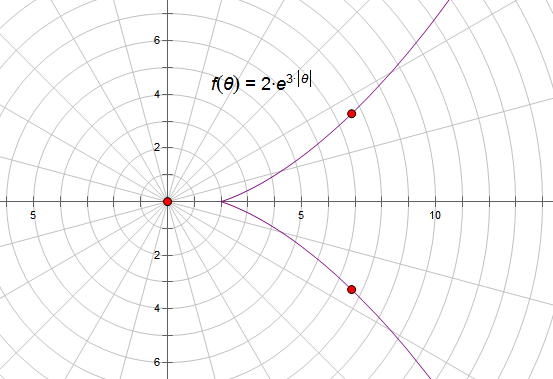
可以进一步化简成$r=Ae^{B|\theta|}$的形式。其形状如下图：

新悬链线

新悬链线

转载到请包括本文地址：https://kexue.fm/archives/1361

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (May. 15, 2011). 《地球引力场的悬链线方程 》[Blog post]. Retrieved from https://kexue.fm/archives/1361

@online{kexuefm-1361,
        title={地球引力场的悬链线方程},
        author={苏剑林},
        year={2011},
        month={May},
        url={\url{https://kexue.fm/archives/1361}},
}