23
Oct
2011年全国高中数学联赛
By 苏剑林 | 2011-10-23 | 34941位读者 | 引用
18
Nov
[欧拉数学]黎曼ζ函数
By 苏剑林 | 2011-11-18 | 50122位读者 | 引用欧拉数学的魅力在于，它运用类比的方法，把各个看似毫无关联的领域联系了起来，生动而巧妙地得出了正确的结果。他对$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...=\frac{\pi^2}{6}$的计算便是一个典型的例子。虽然论证过程未必严谨，但是那“神奇”的推导已经令我们拍案叫绝，而且往往发人深思。这种效果通常是严格论证难以实现的，它不仅给予我们答案，而且还给予了我们启迪：新的思想，新的方向；有时，它还揭示了各个学科之间内在而深刻的联系。下面我们来观察一下数论中的“黎曼ζ函数”和“金钥匙”！
黎曼ζ函数指的是：
$$\xi (s)=\sum_{n=1}^{\infty} \frac{1}{n^s}=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+...$$
本来s应该是一个实数，但是将复分析引入数论后，将s推广至复数具有更大的研究价值。
19
Nov
[欧拉数学]素数倒数之和
By 苏剑林 | 2011-11-19 | 37745位读者 | 引用上一篇文章我通过欧拉数学的方式简单地讲了数论中的“黎曼ζ函数”和“金钥匙”。事实上，这把“金钥匙”与很多问题之间的联系已经被建立了起来，换句话说，“金钥匙”已经插入到了相应的“锁孔”中，数学家的工作就是要把这个金钥匙“拧动”，继而打开数学之门！
接下来我们看看如何证明所有素数的倒数之和发散的。在入正题之前，我们得需要看一个引理：
无限数列${a_n}$的每一项都大于0，那么$\sum\limits_{n=1}^{\infty} a_n$与$\prod\limits_{n=1}^{\infty} \left(1+a_n\right)$的敛散性相同。换句话说，两者互为充分必要条件！
30
Jun
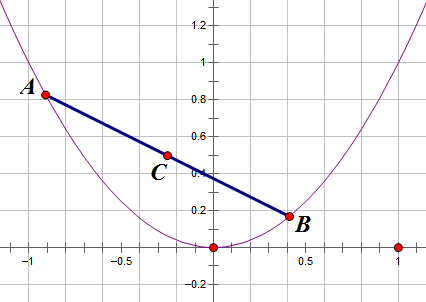
抛物线内一根定长的弦
By 苏剑林 | 2012-06-30 | 32298位读者 | 引用
今天傍晚看到了彩虹！当然这算不上什么奇观，但还是一道美丽的风景。
人说“不经历风雨，怎么见彩虹”，我发现彩虹不一定是在雨后的，今天我看彩虹的时候，就是暴风雨前夕。彩虹是在18点10分左右出现的，持续了5分钟左右吧，看着看着，雨越下越大，我被迫停止欣赏了，不过彩虹也随之消失了。
用一个老相机简单记录了一下这道亮丽的风景！这是我第一次拍摄彩虹^_^
不知道是相机问题还是真有其事，在照片上发现有两条彩虹。难道这次的彩虹是”双彩虹“？那可真是奇观了！
很老的家用数码相机，没有广角，不能拍摄全景，这是用photoshop把两张图片拼凑起来的，效果不好
最近评论