3
May
从动力学角度看优化算法（四）：GAN的第三个阶段
By 苏剑林 | 2019-05-03 | 101773位读者 | 引用在对GAN的学习和思考过程中，我发现我不仅学习到了一种有效的生成模型，而且它全面地促进了我对各种模型各方面的理解，比如模型的优化和理解视角、正则项的意义、损失函数与概率分布的联系、概率推断等等。GAN不单单是一个“造假的玩具”，而是具有深刻意义的概率模型和推断方法。
作为事后的总结，我觉得对GAN的理解可以粗糙地分为三个阶段：
1、样本阶段：在这个阶段中，我们了解了GAN的“鉴别者-造假者”诠释，懂得从这个原理出发来写出基本的GAN公式（如原始GAN、LSGAN），比如判别器和生成器的loss，并且完成简单GAN的训练；同时，我们知道GAN有能力让图片更“真”，利用这个特性可以把GAN嵌入到一些综合模型中。
2、分布阶段：在这个阶段中，我们会从概率分布及其散度的视角来分析GAN，典型的例子是WGAN和f-GAN，同时能基本理解GAN的训练困难问题，比如梯度消失和mode collapse等，甚至能基本地了解变分推断，懂得自己写出一些概率散度，继而构造一些新的GAN形式。
3、动力学阶段：在这个阶段中，我们开始结合优化器来分析GAN的收敛过程，试图了解GAN是否能真的达到理论的均衡点，进而理解GAN的loss和正则项等因素如何影响的收敛过程，由此可以针对性地提出一些训练策略，引导GAN模型到达理论均衡点，从而提高GAN的效果。
19
Oct
最小熵原理（五）：“层层递进”之社区发现与聚类
By 苏剑林 | 2019-10-19 | 163325位读者 | 引用让我们不厌其烦地回顾一下：最小熵原理是一个无监督学习的原理，“熵”就是学习成本，而降低学习成本是我们的不懈追求，所以通过“最小化学习成本”就能够无监督地学习出很多符合我们认知的结果，这就是最小熵原理的基本理念。
这篇文章里，我们会介绍一种相当漂亮的聚类算法，它同样也体现了最小熵原理，或者说它可以通过最小熵原理导出来，名为InfoMap，或者MapEquation。事实上InfoMap已经是2007年的成果了，最早的论文是《Maps of random walks on complex networks reveal community structure》，虽然看起来很旧，但我认为它仍是当前最漂亮的聚类算法，因为它不仅告诉了我们“怎么聚类”，更重要的是给了我们一个“为什么要聚类”的优雅的信息论解释，并从这个解释中直接导出了整个聚类过程。
一个复杂有向图网络示意图。图片来自InfoMap最早的论文《Maps of random walks on complex networks reveal community structure》
当然，它的定位并不仅仅局限在聚类上，更准确地说，它是一种图网络上的“社区发现”算法。所谓社区发现（Community Detection），大概意思是给定一个有向/无向图网络，然后找出这个网络上的“抱团”情况，至于详细含义，大家可以自行搜索一下。简单来说，它跟聚类相似，但是比聚类的含义更丰富。（还可以参考《什么是社区发现?》）
29
Jun
基于Bert的NL2SQL模型：一个简明的Baseline
By 苏剑林 | 2019-06-29 | 149439位读者 | 引用在之前的文章《当Bert遇上Keras：这可能是Bert最简单的打开姿势》中，我们介绍了基于微调Bert的三个NLP例子，算是体验了一把Bert的强大和Keras的便捷。而在这篇文章中，我们再添一个例子：基于Bert的NL2SQL模型。
NL2SQL的NL也就是Natural Language，所以NL2SQL的意思就是“自然语言转SQL语句”，近年来也颇多研究，它算是人工智能领域中比较实用的一个任务。而笔者做这个模型的契机，则是今年我司举办的首届“中文NL2SQL挑战赛”：
首届中文NL2SQL挑战赛，使用金融以及通用领域的表格数据作为数据源，提供在此基础上标注的自然语言与SQL语句的匹配对，希望选手可以利用数据训练出可以准确转换自然语言到SQL的模型。
这个NL2SQL比赛算是今年比较大型的NLP赛事了，赛前投入了颇多人力物力进行宣传推广，比赛的奖金也颇丰富，唯一的问题是NL2SQL本身算是偏冷门的研究领域，所以注定不会太火爆，为此主办方也放出了一个Baseline，基于Pytorch写的，希望能降低大家的入门难度。
抱着“Baseline怎么能少得了Keras版”的心态，我抽时间自己用Keras做了做这个比赛，为了简化模型并且提升效果也加载了预训练的Bert模型，最终形成此文。
3
Sep
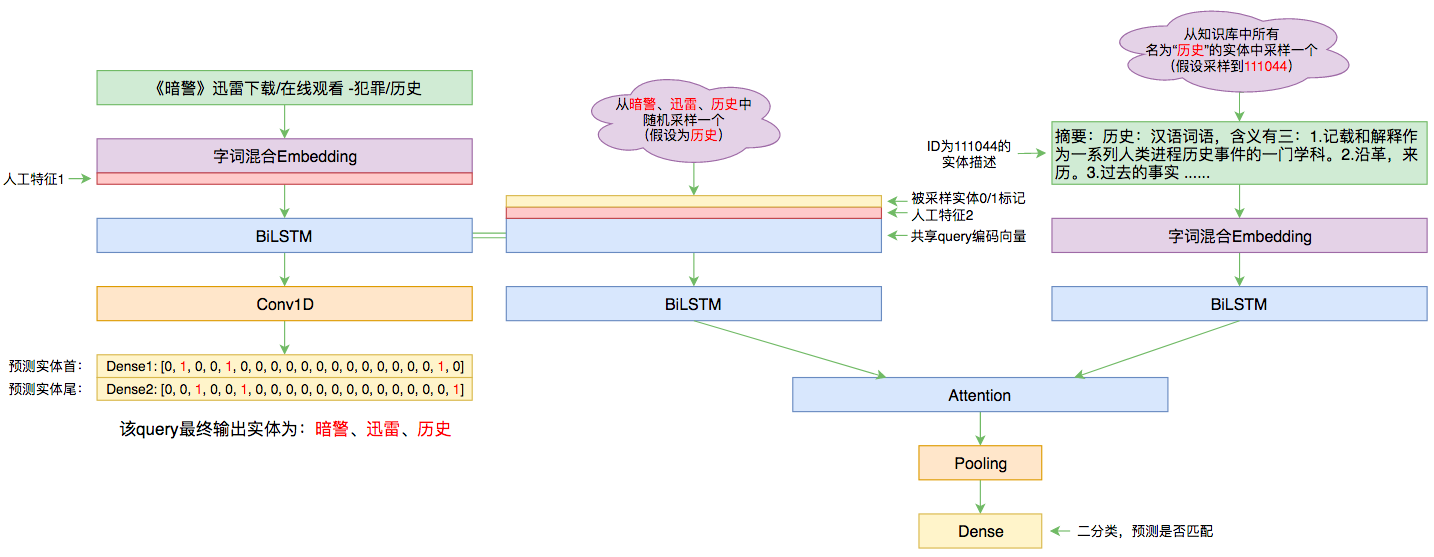
百度实体链接比赛后记：行为建模和实体链接
By 苏剑林 | 2019-09-03 | 91336位读者 | 引用前几个月曾参加了百度的实体链接比赛，这是CCKS2019的评测任务之一，官方称之为“实体链指”，比赛于前几个星期完全结束。笔者最终的F1是0.78左右（冠军是0.80），排在第14名，成绩并不突出（唯一的特色是模型很轻量级，GTX1060都可以轻松跑起来），所以本文只是纯粹的记录过程，大牛们请一笑置之～
本文的实体链接模型总图（可以点击查看大图）
赛题介绍
所谓实体链接，主要指的是在已有一个知识库的情况下，预测输入query的某个实体对应知识库id。也就是说，知识库里边记录了很多实体，对于同一个名字的实体可能会有多个解释，每个解释用一个唯一id编号，我们要做的就是预测query中的实体究竟对应哪一个解释（id）。这是基于知识图谱的问答系统的必要步骤。
1
Mar
对抗训练浅谈：意义、方法和思考（附Keras实现）
By 苏剑林 | 2020-03-01 | 240638位读者 | 引用当前，说到深度学习中的对抗，一般会有两个含义：一个是生成对抗网络（Generative Adversarial Networks，GAN），代表着一大类先进的生成模型；另一个则是跟对抗攻击、对抗样本相关的领域，它跟GAN相关，但又很不一样，它主要关心的是模型在小扰动下的稳健性。本博客里以前所涉及的对抗话题，都是前一种含义，而今天，我们来聊聊后一种含义中的“对抗训练”。
本文包括如下内容：
1、对抗样本、对抗训练等基本概念的介绍；
2、介绍基于快速梯度上升的对抗训练及其在NLP中的应用；
3、给出了对抗训练的Keras实现（一行代码调用）；
4、讨论了对抗训练与梯度惩罚的等价性；
5、基于梯度惩罚，给出了一种对抗训练的直观的几何理解。
10
Jun
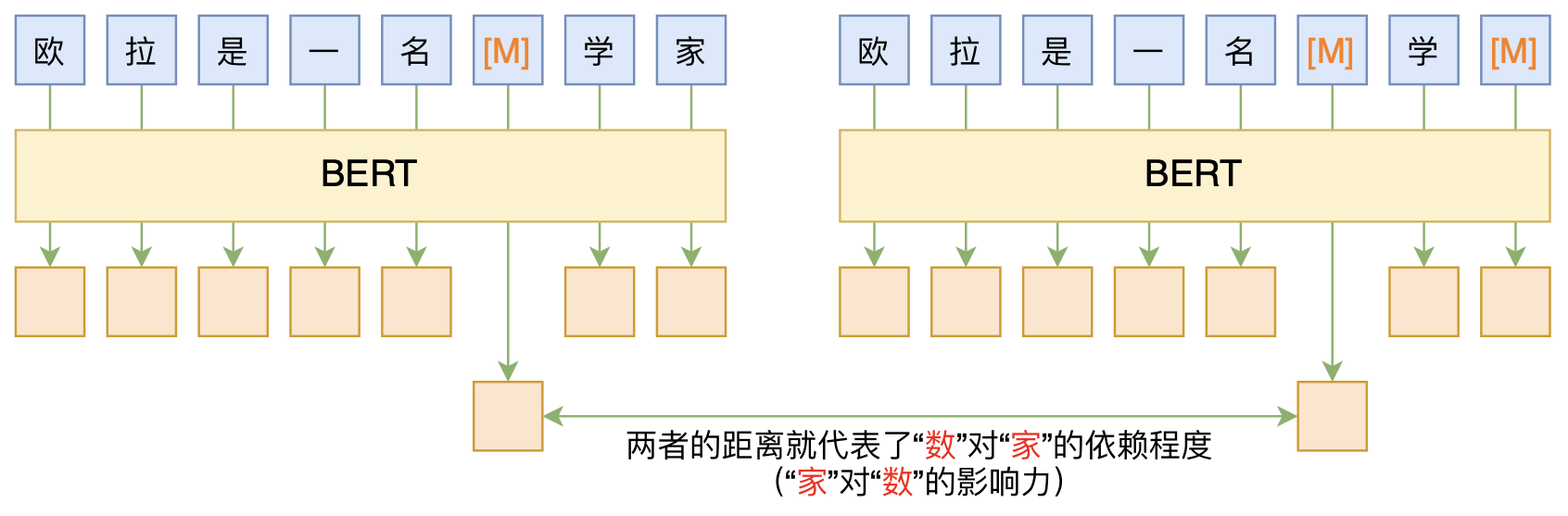
无监督分词和句法分析！原来BERT还可以这样用
By 苏剑林 | 2020-06-10 | 90171位读者 | 引用BERT的一般用法就是加载其预训练权重，再接一小部分新层，然后在下游任务上进行finetune，换句话说一般的用法都是有监督训练的。基于这个流程，我们可以做中文的分词、NER甚至句法分析，这些想必大家就算没做过也会有所听闻。但如果说直接从预训练的BERT（不finetune）就可以对句子进行分词，甚至析出其句法结构出来，那应该会让人感觉到意外和有趣了。
本文介绍ACL 2020的论文《Perturbed Masking: Parameter-free Probing for Analyzing and Interpreting BERT》，里边提供了直接利用Masked Language Model（MLM）来分析和解释BERT的思路，而利用这种思路，我们可以无监督地做到分词甚至句法分析。
基于BERT的“token-token”相关度计算图示
10
Jul
强大的NVAE：以后再也不能说VAE生成的图像模糊了
By 苏剑林 | 2020-07-10 | 119038位读者 | 引用昨天早上，笔者在日常刷arixv的时候，然后被一篇新出来的论文震惊了！论文名字叫做《NVAE: A Deep Hierarchical Variational Autoencoder》，顾名思义是做VAE的改进工作的，提出了一个叫NVAE的新模型。说实话，笔者点进去的时候是不抱什么希望的，因为笔者也算是对VAE有一定的了解，觉得VAE在生成模型方面的能力终究是有限的。结果，论文打开了，呈现出来的画风是这样的：
NVAE的人脸生成效果
然后笔者的第一感觉是这样的：
W!T!F! 这真的是VAE生成的效果？这还是我认识的VAE么？看来我对VAE的认识还是太肤浅了啊，以后再也不能说VAE生成的图像模糊了...
15
Sep
殊途同归的策略梯度与零阶优化
By 苏剑林 | 2020-09-15 | 60208位读者 | 引用深度学习如此成功的一个巨大原因就是基于梯度的优化算法（SGD、Adam等）能有效地求解大多数神经网络模型。然而，既然是基于梯度，那么就要求模型是可导的，但随着研究的深入，我们时常会有求解不可导模型的需求，典型的例子就是直接优化准确率、F1、BLEU等评测指标，或者在神经网络里边加入了不可导模块（比如“跳读”操作）。
Gradient
本文将简单介绍两种求解不可导的模型的有效方法：强化学习的重要方法之一策略梯度（Policy Gradient），以及干脆不需要梯度的零阶优化（Zeroth Order Optimization）。表面上来看，这是两种思路完全不一样的优化方法，但本文将进一步证明，在一大类优化问题中，其实两者基本上是等价的。
最近评论