“十字架”组合计数问题浅试

昨天在这个公众号文章看到了一道据说答案有争议的“十字架”组合计数问题：

一个正方形中，如果四条边有两条是$i$色，另外两条是其他两种不同颜色，那么称这个正方形是“$i$色主导”的。考虑如下由16条线段、5个正方形组成的“十字架”图形，每条边染上红、黄、蓝三色之一，使得横向和竖向三个正方形的主导色均不相同，问有多少种不同的染色方法。

“十字架”示意图

链接的文章有两个答案：吴康老师的54432，以及王慧兴老师的27216。本文先通过编程确认王慧兴老师的27216是正确答案，然后给出自己的理论分析过程。

编程验证 #

这种数目不大的排列组合题，最简单直接验证答案正确与否的方式自然是编程枚举了。最直接的编程方式是枚举16条线段所有可能的染色方案，然后逐一判断是否符合要求。不过这个方案需要枚举$3^{16}\approx 4300\text{万}$个方案，计算量还是蛮大的，因此可以想点办法降低一下计算量。

首先，我们自然地将五个正方形标记为“上”、“下”、“左”、“右”、“中”，如下图：

“十字架”的自然分区标记

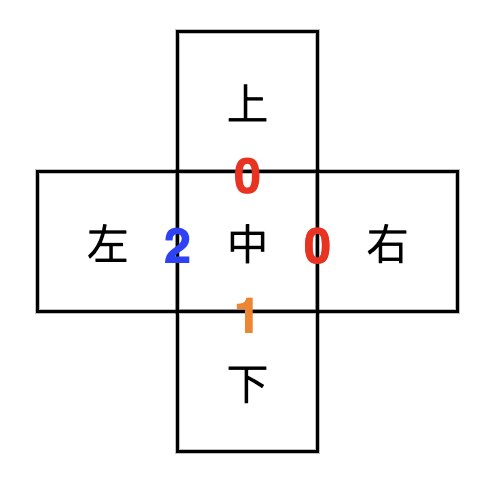
很明显，在这五个正方形中，“中”的地位最特殊，所以不管是理论分析还是编程计算，我们都以它为出发点。为了编程的方便，我们将红、黄、蓝三种颜色分别对应于0、1、2三个数字。于是，我们可以很快枚举出“中”的所有可能染色方案为：

from itertools import product

centers = [s for s in product(*[range(3)] * 4) if len(set(s)) == 3]

然后，我们对每一种“中”的染色方案，枚举其对应的“上”、“下”、“左”、“右”染色方案，方法也很简单，先识别出“中”染色的主导色，然后“上-下”、“左-右”的主导色分别从剩下两种颜色取，将“上”、“下”、“左”、“右”的染色方案数乘起来就行了，要注意给定“中”染色方案后，在枚举“上”、“下”、“左”、“右”方案时，它们都有一条边的染色已经被确定，所以可枚举的数目应该是$3^3$而不是$3^4$。总的参考代码如下：

def master(s):
    """识别主导色
    """
    for i in range(3):
        if s.count(i) == 2:
            return i

N = 0
for c in centers:
    m = master(c)  # 当前主导色
    M = [i for i in range(3) if i != m]  # 剩余两种颜色
    for i in range(2):  # 上、下主导色
        for j in range(2):  # 左、右主导色
            top = [s for s in product([c[0]], *[range(3)] * 3) if len(set(s)) == 3 and master(s) == M[i]]
            bottom = [s for s in product([c[2]], *[range(3)] * 3) if len(set(s)) == 3 and master(s) == M[1 - i]]
            left = [s for s in product([c[1]], *[range(3)] * 3) if len(set(s)) == 3 and master(s) == M[j]]
            right = [s for s in product([c[3]], *[range(3)] * 3) if len(set(s)) == 3 and master(s) == M[1 - j]]
            N += len(top) * len(bottom) * len(left) * len(right)

print(u'总染色方案数为', N)

最后得出总染色方案数为27216。

理论计算 #

从理论角度来计算最终的染色方案数，其思路跟实验验证是一样的，都是先中间后两边，只不过把代码中暴力枚举部分通过排列组合公式来计算。

首先，还是“中”的染色方案数，看组合的话，有“0 0 1 2”、“0 1 1 2”和“0 1 2 2”三种。以“0 0 1 2”为例，在“0 0”中插入一个1，有3个位置可选，然后再插入一个2，有4个位置可选，所以每种组合有$3\times 4=12$中排列，因此“中”的染色方案数就是$12\times 3 = 36$。

接着，我们将“中”的染色方案分为如下图的两类：1、两个主导色相邻；2、两个主导色相对。

“中”的方案一：主导色相邻

“中”的方案二：主导色相对

很明显，两者的占比为2:1，因此“中”的染色方案中，主导色相邻的有24种，主导色相对的有12种，下面分别讨论这两种情况。

第一，主导色相邻，不失一般性我们就考虑上图左的情况，此时“中”的主导色是“红”，因此“上”、“下”两个主导色只能选“黄”或“蓝”。假设“上”的主导色选“黄”，那么它的染色方案只有3种，而相应地“下”的染色方案也只有3种，因此“上-下”共有$3\times 3=9$种染色方案；如果“上”的主导色选“蓝”，那么它的染色方案也只有3种，但相应地“下”的染色方案有6种，因此“上-下”共有$3\times 6=18$种染色方案。两种情况加起来就是$9+18=27$种方案，“左-右”的分析结果也是一样的，并且“上-下”和“左-右”可以随意组合，因此共有$27\times 27=729$种方案。注意这只是其中一种“中”染色方案对应的“上”、“下”、“左”、“右”方案，所以此种情况下所有染色方案总数就是$729\times 24=17496$种。

第二，主导色相对，不失一般性我们就考虑上图右的情况，此时“中”的主导色是“红”，因此“上”、“下”两个主导色只能选“黄”或“蓝”。假设“上”的主导色选“黄”，那么它的染色方案只有3种，而相应地“下”的染色方案也只有3种，因此“上-下”共有$3\times 3=9$种染色方案；如果“上”的主导色选“蓝”，那么它的染色方案也只有3种，“下”的染色方案同样只有3种，因此“上-下”共有$3\times 3=9$种染色方案。两种情况加起来就是$9+9=18$种方案。

但此种情况下，“左-右”的结果跟“上-下”是不一样的，需要另外分析。假设“左”的主导色选“黄”，那么它的染色方案只有3种，而相应地“右”的染色方案也只有3种，因此“左-右”共有$3\times 3=9$种染色方案；如果“左”的主导色选“蓝”，那么它的染色方案就有6种，“右”的染色方案同样有6种，因此“左-右”共有$6\times 6=36$种染色方案。两种情况加起来就是$9+36=45$种方案。所以“上”、“下”、“左”、“右”、“中”总的染色方案数就是$18\times 45\times 12=9720$种。

最后，两者加起来就是$17496+9720=27216$种。

文章小结 #

好久没做数学题了，纯粹温习一下高中数学知识～

转载到请包括本文地址：https://kexue.fm/archives/9291

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。