CoSENT(一):比Sentence-BERT更有效的句向量方案
By 苏剑林 | 2022-01-06 | 360040位读者 |学习句向量的方案大致上可以分为无监督和有监督两大类,其中有监督句向量比较主流的方案是Facebook提出的“InferSent”,而后的“Sentence-BERT”进一步在BERT上肯定了它的有效性。然而,不管是InferSent还是Sentence-BERT,它们在理论上依然相当令人迷惑,因为它们虽然有效,但存在训练和预测不一致的问题,而如果直接优化预测目标cos值,效果往往特别差。
最近,笔者再次思考了这个问题,经过近一周的分析和实验,大致上确定了InferSent有效以及直接优化cos值无效的原因,并提出了一个优化cos值的新方案CoSENT(Cosine Sentence)。实验显示,CoSENT在收敛速度和最终效果上普遍都比InferSent和Sentence-BERT要好。
朴素思路 #
本文的场景是利用文本匹配的标注数据来构建句向量模型,其中所利用到的标注数据是常见的句子对样本,即每条样本是“(句子1, 句子2, 标签)”的格式,它们又大致上可以分类“是非类型”、“NLI类型”、“打分类型”三种,参考《用开源的人工标注数据来增强RoFormer-Sim》中的“分门别类”一节。
失效的Cos #
简单起见,我们可以先只考虑“是非类型”的数据,即“(句子1, 句子2, 是否相似)”的样本。假设两个句子经过编码模型后分别得到向量$u,v$,由于检索阶段计算的是余弦相似度$\cos(u,v)=\frac{\langle u,v\rangle}{\Vert u\Vert \Vert v\Vert}$,所以比较自然的想法是设计基于$\cos(u,v)$的损失函数,比如
\begin{align}t\cdot (1 - \cos(u, v)) + (1 - t) \cdot (1 + \cos(u,v))\label{eq:cos-1}\\
t\cdot (1 - \cos(u, v))^2 + (1 - t) \cdot \cos^2(u,v)\label{eq:cos-2}
\end{align}
其中$t\in\{0,1\}$表示是否相似。类似的loss还可以写出很多,大致的意思都是让正样本对的相似度尽可能大、负样本对的相似度尽可能小。然而,直接优化这些目标的实验结果往往特别差(至少明显比InferSent要差),在某些情况下甚至还不如随机初始化的效果。
难搞的阈值 #
这是因为,通常文本匹配语料中标注出来的负样本对都是“困难样本”,常见的是语义不相同但字面上有比较多的重合。此时,如果我们用式$\eqref{eq:cos-1}$作为损失函数,那么正样本对的目标是1、负样本对的目标是-1,如果我们用式$\eqref{eq:cos-2}$作为损失函数,那么正样本对的目标是1、负样本对的目标是0。不管哪一种,负样本对的目标都“过低”了,因为对于“困难样本”来说,虽然语义不同,但依然是“相似”,相似度不至于0甚至-1那么低,如果强行让它们往0、-1学,那么通常的后果就是造成过度学习,从而失去了泛化能力,又或者是优化过于困难,导致根本学不动。
要验证这个结论很简单,只需要把训练集的负样本换成随机采样的样本对(视作更弱的负样本对),然后用上述loss进行训练,就会发现效果反而会变好。如果不改变负样本对,那么缓解这个问题的一个方法是给负样本对设置更高的阈值,比如
\begin{equation}t\cdot (1 - \cos(u, v)) + (1 - t) \cdot \max(\cos(u,v),0.7)\end{equation}
这样一来,负样本对的相似度只要低于0.7就不优化了,从而就不那么容易过度学习了。但这仅仅是缓解,效果也很难达到最优,而且如何选取这个阈值依然是比较困难的问题。
InferSent #
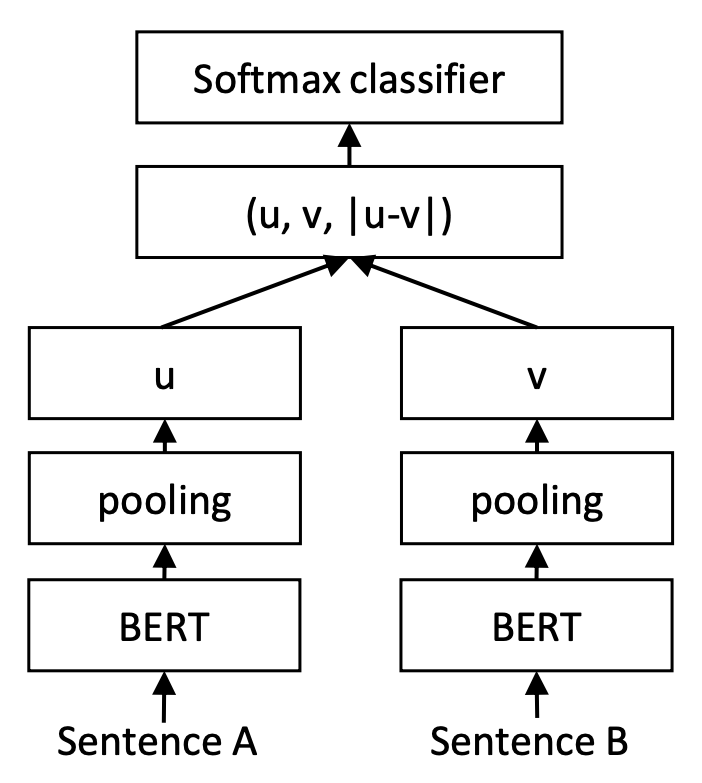
让人倍感神奇的是,训练和预测不一致的InferSent和Sentence-BERT,却在这个问题上表现良好。以Sentence-BERT为例,它的训练阶段是将$u,v,|u−v|$(其中$|u−v|$是指$u−v$的每个元素都取绝对值后构成的向量)拼接起来做为特征,后面接一个全连接层做2分类(如果是NLI数据集则是3分类),而在预测阶段,还是跟普通的句向量模型一样,先计算句向量然后算cos值作为相似度。如下图所示:
再闭门造车 #
为什么InferSent和Sentence-BERT会有效?在《用开源的人工标注数据来增强RoFormer-Sim》中的“闭门造车”一节笔者给出了一个基于容错性的解释,而经过这段时间的思考,笔者对这个问题有了一个新的理解,这里再跟大家分享交流一下。
一般情况下,哪怕负样本对是“困难样本”,总体而言正样本对的字面相似度是大于负样本对的,这样一来,哪怕是对于初始模型,正样本对的差距$\Vert u-v\Vert$总体较小,而负样本对的差距$\Vert u-v\Vert$总体较大,我们可以想象正样本对的$u-v$主要分布在一个半径较小的球面附近,而负样本对的$u-v$分布在一个半径较大的球面附近,也就是说,初始阶段$u-v$本身就有聚类倾向,我们接下来只需要根据标签信息强化这种聚类倾向,使得正样本对的$u-v$依然保持更小,负样本对的$u-v$保持更大。一个直接的做法就是$u-v$后面接一个Dense分类器,然而常规的分类器是基于内积的,它没法区分两个分布在不同球面的类别,所以我们加上绝对值变成$|u-v|$,将球面变为局部的球盖(或者说将球体变成锥形),此时就可以用Dense分类层来分类了。这就是笔者认为的$|u-v|$的来源。
至于$u,v$的拼接,笔者认为是用来消除各向异性的。像“BERT+[CLS]”的句向量模型,在初始阶段具有严重的各向异性,这种各向异性对句向量的效果有着比较严重的负面影响,而$|u-v|$只是向量的相对差距,无法明显改善这种各向异性。而$u,v$拼接之后接Dense层,由于Dense层的类别向量是随机初始化的,所以相当于给了$u,v$一个随机的优化方向,迫使它们各自“散开”,远离当前的各向异性状态。
潜在的问题 #
InferSent和Sentence-BERT虽然有效,但也存在比较明显的问题。
比如,前面说了它有效的原因是初始阶段就有聚类倾向,而标签训练只是强化这个聚类倾向信息,所以“初始阶段就有聚类倾向”就显得相当重要,它意味着其效果比较依赖于初始模型,比如“BERT+平均池化”的最终效果就优于“BERT+[CLS]”,因为前者在初始阶段的区分度就更好。
此外,InferSent和Sentence-BERT终究是训练和预测不一致的方案,所以存在一定的概率会“训崩”,具体表现为训练loss还在下降,训练acc还在提升,但是基于余弦值的评测指标(如Spearman系数)却明显下降,哪怕是训练集也是如此。这说明训练还是正常进行的,但是已经脱离了“正样本对的$u-v$更小、负样本对的$u-v$更大”的分类依据,从而余弦值就崩了。
InferSent和Sentence-BERT还存在调优困难问题,这同样是因为训练和预测的不一致性,导致我们很难确定对哪些训练过程的调整会给预测结果带来正面帮助。
CoSENT #
简单来说,就是InferSent和Sentence-BERT算是一种可用的方案,但存在诸多的不确定性。那难道优化cos值就真的没有出头之日了吗?当然不是。早前的SimCSE其实也有一个有监督版,它也是直接优化cos值,但它要用到“(原始句子, 相似句子, 不相似句子)”格式的三元组数据。而本文提出的CoSENT,则进一步改进了上述思路,使得训练过程只用到句子对样本。
新损失函数 #
我们记$\Omega_{pos}$为所有的正样本对集合,$\Omega_{neg}$为所有的负样本对集合,其实我们是希望对于任意的正样本对$(i,j)\in \Omega_{pos}$和负样本对$(k,l)\in \Omega_{neg}$,都有
\begin{equation}\cos(u_i,u_j) > \cos(u_k, u_l)\end{equation}
其实$u_i,u_j,u_k,u_l$是它们各自的句向量。说白了,我们只希望正样本对的相似度大于负样本对的相似度,至于大多少,模型自己决定就好。事实上语义相似度常见的评价指标spearman也是一样,它只依赖于预测结果的相对顺序,而不依赖于具体的值。
在《将“Softmax+交叉熵”推广到多标签分类问题》中,我们介绍了处理这类需求的一个有效方案,那就是Circle Loss理论里边的公式(1):
\begin{equation}\log \left(1 + \sum\limits_{i\in\Omega_{neg},j\in\Omega_{pos}} e^{s_i-s_j}\right)\end{equation}
简单来说,就是如果你希望最终实现$s_i < s_j$,那么就往$\log$里边加入$e^{s_i-s_j}$一项。对应我们这里的场景,我们可以得到损失函数
\begin{equation}\log \left(1 + \sum\limits_{(i,j)\in\Omega_{pos},(k,l)\in\Omega_{neg}} e^{\lambda(\cos(u_k, u_l) - \cos(u_i, u_j))}\right)\label{eq:cosent}\end{equation}
其中$\lambda > 0$是一个超参数,本文后面的实验取了20。这就是CoSENT的核心内容了,它是一个优化cos值的新的损失函数。
通用的排序 #
可能有读者质疑:就算这里的式$\eqref{eq:cosent}$真的可用,那也只适用于二分类数据,像NLI数据是3分类的就不能用了?
事实上,式$\eqref{eq:cosent}$本质上是一个为排序设计的损失函数,它可以更加通用地写成:
\begin{equation}\log \left(1 + \sum\limits_{\text{sim}(i,j) \gt \text{sim}(k,l)} e^{\lambda(\cos(u_k, u_l) - \cos(u_i, u_j))}\right)\label{eq:cosent-2}\end{equation}
也就是说,只要我们认为样本对$(i,j)$的真实相似度应该大于$(k,l)$的真实相似度,就可以往$\log$里边加入$e^{\lambda(\cos(u_k, u_l) - \cos(u_i, u_j))}$;换句话说,只要我们能够为样本对设计顺序,那么就可以用式$\eqref{eq:cosent-2}$
对于NLI数据而言,它有“蕴含”、“中立”、“矛盾”三种标签,我们自然可以认为两个“蕴含”的句子相似度大于两个“中立”的句子,而两个“中立”的句子相似度大于两个“矛盾”的句子,这样基于这三种标签就可以为NLI的句子对排序了。而有了这个排序后,NLI数据也可以用CoSENT来训练了。类似地,对于STS-B这种本身就是打分的数据,就更适用于CoSENT了,因为打分标签本身就是排序信息。
当然,如果多类别之间没有这种序关系,那就不能用CoSENT了。然而,对于无法构建序关系的多类别句子对数据,InferSent和Sentence-BERT能否出合理的句向量模型,笔者也是持怀疑态度。目前没看到类似的数据集,也就无从验证了。
优秀的效果 #
笔者在多个中文数据集上对CoSENT进行了实验,分别比较了在原有训练集上训练以及在NLI数据集训练两种方案,大多数实验结果都表明CoSENT明显优于Sentence-BERT。测试数据集同《无监督语义相似度哪家强?我们做了个比较全面的评测》,每个数据集都被划分为train、valid、test三部分,评测指标是预测值和标签的spearman系数。
下面是用各自的train集进行训练后,test集的效果:
\begin{array}{c|ccccc|c}
\hline
& \text{ATEC} & \text{BQ} & \text{LCQMC} & \text{PAWSX} & \text{STS-B} & \text{Avg}\\
\hline
\text{BERT+CoSENT} & \textbf{49.74} & \textbf{72.38} & 78.69 & \textbf{60.00} & \textbf{80.14} & \textbf{68.19}\\
\text{Sentence-BERT} & 46.36 & 70.36 & \textbf{78.72} & 46.86 & 66.41 & 61.74\\
\hline
\text{RoBERTa+CoSENT} & \textbf{50.81} & \textbf{71.45} & \textbf{79.31} & \textbf{61.56} & \textbf{81.13}
& \textbf{68.85}\\
\text{Sentence-RoBERTa} & 48.29 & 69.99 & 79.22 & 44.10 & 72.42 & 62.80\\
\hline
\end{array}
下面则是用开源的NLI数据作为训练集进行训练后,每个任务的test集的效果:
\begin{array}{c|ccccc|c}
\hline
& \text{ATEC} & \text{BQ} & \text{LCQMC} & \text{PAWSX} & \text{STS-B} & \text{Avg}\\
\hline
\text{BERT+CoSENT} & \textbf{28.93} & 41.84 & \textbf{66.07} & \textbf{20.49} & 73.91 & \textbf{46.25} \\
\text{Sentence-BERT} & 28.19 & \textbf{42.73} & 64.98 & 15.38 & \textbf{74.88} & 45.23 \\
\hline
\text{RoBERTa+CoSENT} & 31.84 & \textbf{46.65} & \textbf{68.43} & \textbf{20.89} & \textbf{74.37} & \textbf{48.43}\\
\text{Sentence-RoBERTa} & \textbf{31.87} & 45.60 & 67.89 & 15.64 & 73.93 & 46.99\\
\hline
\end{array}
可以看到,大多数任务上CoSENT都有较为明显的提升,而个别有任务上的下降也是比较小的(1%以内),原生训练的平均提升幅度超过6%,而NLI训练的平均提升幅度也有1%左右。
此外,CoSENT还有更快的收敛速度,比如“BERT+CoSENT+ATEC”的原生训练,第一个epoch的valid结果就有48.78,而对应的“Sentence-BERT+ATEC”只有41.54;“RoBERTa+CoSENT+PAWSX”的原生训练,第一个epoch的valid结果就有57.66,而对应的“Sentence-RoBERTa+PAWSX”只有10.84;等等。
联系与区别 #
可能有的读者会问式$\eqref{eq:cosent}$或式$\eqref{eq:cosent-2}$跟SimCSE或对比学习有什么不同?从损失函数的形式上来看两者确有一点相似之处,但含义完全不同的。
标准的SimCSE是只需要正样本对的(通过Dropout或者人工标注构建),然后它将batch内的所有其他样本都视为负样本;而有监督版的SimCSE则是需要三元组的数据,它实际上就是把困难样本补充到标准的SimCSE上,即负样本不只有batch内的所有其他样本,还有标注的困难样本,但同时正样本依然不能缺,所以需要“(原始句子, 相似句子, 不相似句子)”的三元组数据。
至于CoSENT,它只用到了标注好的正负样本对,也不包含随机采样batch内的其他样本来构建负样本的过程,我们也可以将它理解为对比学习,但它是“样本对”的对比学习,而不是像SimCSE的“样本”对比学习,也就是说,它的“单位”是一对句子而不是一个句子。
文章小结 #
本文提出了一种新的有监督句向量方案CoSENT(Cosine Sentence),相比于InferSent和Sentence-BERT,它的训练过程更贴近预测,并且实验显示,CoSENT在收敛速度和最终效果上都普遍比InferSent和Sentence-BERT要好。
转载到请包括本文地址:https://kexue.fm/archives/8847
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jan. 06, 2022). 《CoSENT(一):比Sentence-BERT更有效的句向量方案 》[Blog post]. Retrieved from https://kexue.fm/archives/8847
@online{kexuefm-8847,
title={CoSENT(一):比Sentence-BERT更有效的句向量方案},
author={苏剑林},
year={2022},
month={Jan},
url={\url{https://kexue.fm/archives/8847}},
}










February 16th, 2022
感觉(1),(2)式都是回归的损失,像ATEC, BQ 这类标注是0 或 1, 不太连续,用回归损失本身也不是很合理。 我根据你的结果也自己跑了一下在STS-B和ATEC上的结果,sbert用的损失函数是(2)式,STS-B我把相似度得分除了5。 结果大概如下:
sbert 76.76(sts-b), 19.28(ATEC)
cosenet 80.13(sts-b), 50.40(ATEC)
两个数据集上 cosenet 都是要好不少,但是差距的话, sts-b 比ATEC 的gap就没那么大。 就是感觉像ATEC这种标注为 0 或者 1 的,把样本对看成一个完整样本, 用分类方法判断是正样本还是负样本, 做肯定比用回归效果好,所以对于 (1), (2) 式效果没有 sbert 默认的方式好也是肯定的。
其实我后来分析了,并不是因为回归还是分类的原因,而是对每个样本本身有没有区分度的问题。后面有时间,我会抽空分析一下loss的设计原则,到时候再来继续分析这个问题。
March 7th, 2022
不知道为啥评论一直被吞。。
不太理解为啥不好对比CoSENT和simcse在有监督样本情况下的效果呢?
虽然说一个需要二元组数据,而另一个需要三元组数据。但是两者都可以通过有监督样本创造训练样本进行训练,最后比较再测试集上的F1得分不就可以么?
如果只有二元组数据,如何“创造”三元组数据出来?
如果是“标注的正样本对+随机选取的负样本”,那么负样本太弱,效果不会太好。唯一的可能是通过传递性构建一些出来(如果A、B相似,而B、C不相似,那么A、B、C组合成一个三元组),但这通常情况下无法覆盖所有的二元组,极端情况下一个三元组可能都构造不出来(正样本对和负样本对之间的样本没有重叠),也就是说,这种情况下SimCSE的训练数据不如CoSENT多,比较结果没有说服力。
所以,你说如何公平比较CoSENT和SimCSE在有监督样本情况下的效果?
谢谢苏神的解答,确实无法做到公平
之前想的很简单,就是想说A、B相似则随机找一个c 组成 ABC
A、B不相似,就是A Drop(A) B组成一个三元组
这就用到了无监督的drop想法。构建出的样本确实感觉会很弱,更不公平的感觉了。
March 11th, 2022
苏老师您好,请问可以使用CoSENT去微调RoFormer-sim吗,效果会不会比BERT-CoSENT更好呢
可以的,通常来说会比BERT-CoSENT更好。
苏老师您好,我尝试用CoSENT的方法微调了SimBERT,微调好后加载模型的时候,
```
# 建立加载模型
bert = build_transformer_model(
config_path,
checkpoint_path,
with_pool='linear',
application='unilm',
return_keras_model=False,
)
encoder = keras.models.Model(bert.model.inputs, bert.model.outputs[0])
encoder.load_weights('/Users/xing.sun/Desktop/LCQMC.cosent.weights')
```
报错如下:
```
Traceback (most recent call last):
File "/Users/xing.sun/SentenceEmbedding/reference/simbert/retrieval_test.py", line 31, in
encoder.load_weights('/Users/xing.sun/Desktop/LCQMC.cosent.weights')
File "/Users/xing.sun/.local/lib/python3.6/site-packages/keras/engine/saving.py", line 492, in load_wrapper
return load_function(*args, **kwargs)
File "/Users/xing.sun/.local/lib/python3.6/site-packages/keras/engine/network.py", line 1230, in load_weights
f, self.layers, reshape=reshape)
File "/Users/xing.sun/.local/lib/python3.6/site-packages/keras/engine/saving.py", line 1209, in load_weights_from_hdf5_group
str(len(filtered_layers)) + ' layers.')
**ValueError: You are trying to load a weight file containing 52 layers into a model with 53 layers.**
```
请问这是什么原因呢
怎么保存就怎么加载呀。你微调的时候是怎么建立模型的,那就用同样的方式建立模型,不用抄SimBERT的代码。
March 20th, 2022
您好,我想问一下如果想要引用您的这个模型,该怎么用呢?您已经把它发表为论文了吗?
抱歉,暂时没有论文,可以直接引用本页面。
March 27th, 2022
苏神,在baseline训练余弦相似度时,有没有试过不要归一化,直接用內积
试过,效果没有更好。而且对于CoSENT来说,如果不归一化,那么温度参数更不好设置。
我一开始觉得用cos训不好的原因是它归一化后压缩在模为1的超球面,而emb实际上是在超球体,长度有含义。
但是居然不起作用。
March 28th, 2022
做了一个pytorch实现,写了一个bert4torch的框架,和bert4keras的调用差不过,代码可以参考https://github.com/Tongjilibo/bert4torch/blob/master/examples/sentence_embedding/task_sentence_embedding_CoSENT.py
April 12th, 2022
原文:正样本对的u−v依然保持更小,负样本对的u−v保持更大。一个直接的做法就是u−v后面接一个Dense分类器,然而常规的分类器是基于内积的,它没法区分两个分布在不同球面的类别,所以我们加上绝对值变成|u−v|,将球面变为锥形,此时就可以用Dense分类层来分类了。
苏神,想请教这句,以二维平面为例|u−v|将两个圆形(大小圆)上的向量映射到了第一象限,成为两个扇形。使用向量内积可以理解为将二维扇形上的向量映射到一维空间上的距离,如果简化使用单位向量e来跟两个扇形上的向量做内积,结果可以简化为||a||cos(a,e), ||b||cos(b,e), 其中a,b代表两个扇形(一大一小)上的向量,夹角范围是[0,Π],内积的至于范围分别为[0,||a||],[0,||b||],我理解也是有交集的,为什么Dense分类器不能区分两个球面却能区分两个锥形?
我的理解不是说Dense一定会去区分两个球盖(想了想,因为是面,所以应该叫做球盖而不是锥形),而是球盖消除了各向同性,更有利于Dense的学习。最终它学习出来的问题未必就是在球盖上进行区分两个区域。
球盖消除了各向同性,使向量有了极性,不在均匀分布从而能够区分出来?还是很难想想|u−v|能起到这种作用/(ㄒoㄒ)/~~
这个问题有点复杂。我们只能想象它大概是这样子,并非一定就是这样。
简单起见,我们考虑二维情况,球盖变成圆弧,假如正负样本的$|u-v|$分别集中在$r=1$和$r=2$的圆弧上,角度范围都是$\theta\in[0,\pi/2]$。这时候Dense依然是不能直接将它们分开,但是经过训练后,正样本可能就集中在$r=1,\theta\in[0,pi/8]$的圆弧上,负样本集中在$r=2,\theta\in[3\pi/8,pi/2]$的圆弧上,这时候Dense就能区分开了。
消除各项同性本身就只是一种引导,并非是消除后就能直接区分了。Sentence-BERT怎么看都很玄学,其实我也没法说清它是咋回事。。。
嗯,如果通过训练在角度上有了区隔,确实可以通过内积区分开,但是在两个球面上也可以通过训练实现角度区隔,然后通过向量内积进行区分,可能这里是通过添加绝对值,将空间中分布于多个象限的向量压缩到一个象限上简化了通过训练实现角度变换的难度,然后更容易在分类层上将角度区分开?
我们希望的是原本分散开来的点聚为一簇,你觉得原本分散在整个球面上的点聚为一簇容易,还是分散在某个小球盖的点聚为一簇容易?
我上面的描述来看是位于一个象限的球盖容易一些
May 7th, 2022
你好,苏神。在SBERT论文中有监督STS-B任务中,他使用的是回归目标函数,也就是优化COS值的,也达到了不错的效果,为什么您说直接优化这些目标的实验结果往往特别差。原论文提供了3中训练函数,分类目标函数也一般用于SNLI和NLI,在STS上用的优化COS值的回归目标函数。而且在STS-B任务实验时,应该也是使用优化COS值的回归目标函数,您给出的只使用分类目标函数的SBERT结果是否有点不符合?
首先,我说的结论自然都是我自己的实验结果,不是信口胡诌的,可能其他人训练出来了也说不准,但反正我是训练不出来,另外在群里跟一些网友讨论过,训练不出来的居多。
然后,SBERT的论文,对你说的有监督STS-B是这样描述的:
We use the training set to fine-tune SBERT using the regression objective function. At prediction time, we compute the cosine-similarity between the sentence embeddings.
对于这段话,我没看出它说的是优化cos值,反而更像还是训练时$u,v,|u-v|$拼接在一起但目标是回归而不是二分类、预测时才算cos的做法,要不然它“At prediction time, we compute the cosine-similarity between the sentence embeddings.”这句话就多此一举了。
May 9th, 2022
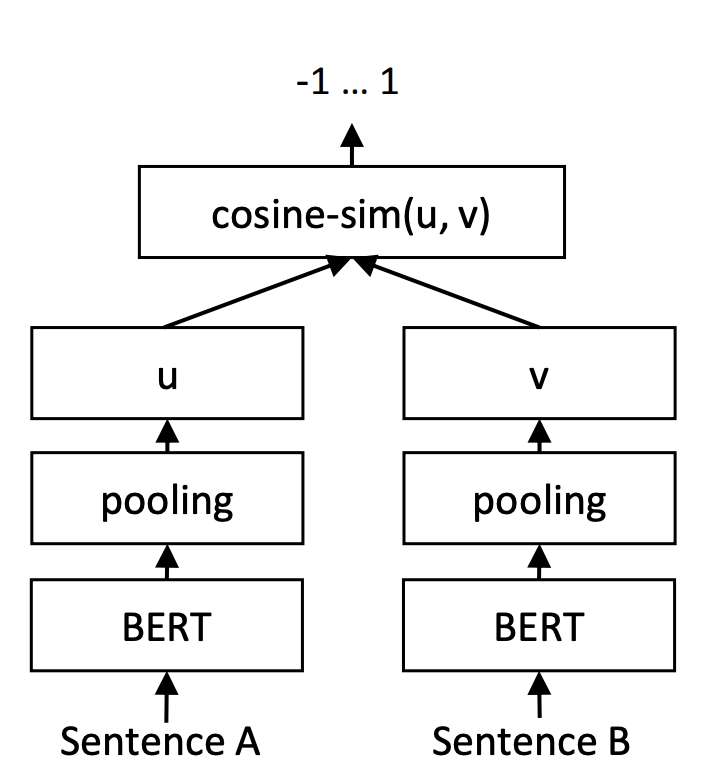
好像不是,Regression Objective Function那一小节说了自己的结构是Figure 2,Figure2的结构就是直接算的cos相似度
哦哦,看到了。那它是在SBERT的基础上微调的,可能SBERT本身就训练得很好了,MSE训练纯粹是锦上添花。我之前的尝试,是直接从BERT出发的,没成功过...
June 21st, 2022
CoSentLoss完全等价于torch版的CrossEntropyLoss?
没看到任何等价之处。