SquarePlus：可能是运算最简单的ReLU光滑近似

ReLU函数，也就是$\max(x,0)$，是最常见的激活函数之一，然而它在$x=0$处的不可导通常也被视为一个“槽点”。为此，有诸多的光滑近似被提出，比如SoftPlus、GeLU、Swish等，不过这些光滑近似无一例外地至少都使用了指数运算$e^x$（SoftPlus还用到了对数），从“精打细算”的角度来看，计算量还是不小的（虽然当前在GPU加速之下，我们很少去感知这点计算量了）。最近有一篇论文《Squareplus: A Softplus-Like Algebraic Rectifier》提了一个更简单的近似，称为SquarePlus，我们也来讨论讨论。

需要事先指出的是，笔者是不建议大家花太多时间在激活函数的选择和设计上的，所以虽然分享了这篇论文，但主要是提供一个参考结果，并充当一道练习题来给大家“练练手”。

定义 #

SquarePlus的形式很简单，只用到了加、乘、除和开方：
\begin{equation}\text{SquarePlus}(x)=\frac{x+\sqrt{x^2+b}}{2}\end{equation}
其中$b > 0$。当$b=0$时，正好退化为$\text{ReLU}(x)=\max(x,0)$。SquarePlus的灵感来源大致是
\begin{equation}\max(x,0)=\frac{x+|x|}{2}=\frac{x+\sqrt{x^2}}{2}\end{equation}
因此为了补充在$x=0$的可导性，在根号里边多加一个大于0的常数$b$（防止导数出现除零问题）。

原论文指出，由于只用到了加、乘、除和开方，所以SquarePlus的速度（主要是在CPU上）会比SoftPlus等函数要快：

当然，如果你不关心这点速度提升，那么就像本文开头说的，当作数学练习题来看看就好。

性态 #

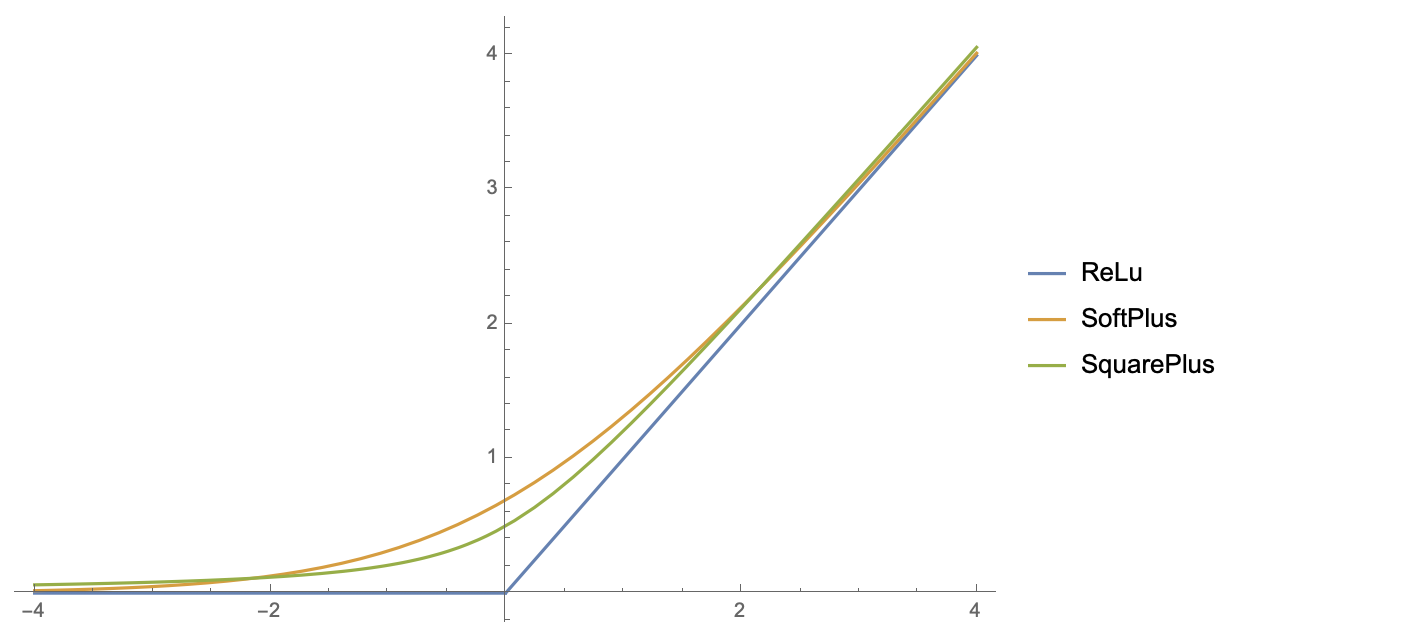
跟SoftPlus函数（$\log(e^x+1)$）一样，SquarePlus也是全局单调递增的，并且恒大于ReLU，如下图（下图的SquarePlus的$b=1$）：

直接求它的导函数也可以看出单调性：
\begin{equation}\frac{d}{dx}\text{SquarePlus}(x)=\frac{1}{2}\left(1+\frac{x}{\sqrt{x^2+b}}\right) > 0\end{equation}
至于二阶导数
\begin{equation}\frac{d^2}{dx^2}\text{SquarePlus}(x)=\frac{b}{2(x^2+b)^{3/2}}\end{equation}
也是恒大于0的存在，所以SquarePlus还是一个凸函数。

逼近 #

现在有两道练习题可以做了：

1、当$b$取什么时SquarePlus恒大于SoftPlus？

2、当$b$取什么时，SquarePlus与SoftPlus误差最小？

第一个问题，直接从$\text{SquarePlus}(x)\geq \text{SoftPlus}(x)$解得：
\begin{equation}b\geq 4\log(e^x+1)\left[\log(e^x+1) - x\right]=4\log(e^x+1)\log(e^{-x}+1)\end{equation}
要使得上式恒成立，$b$必须大于等于右端的最大值，而我们可以证明右端最大值在$x=0$处取到，所以$b\geq 4\log^2 2=1.921812\cdots$。至此，第一个问题解决。

证明：留意到
\begin{equation}
\frac{d^2}{dx^2}\log\log(e^x+1)=\frac{e^x(\log(e^x+1)-e^x)}{(e^x+1)^2\log^2(e^x+1)} < 0\end{equation}

所以$\log\log(e^x+1)$是一个凹函数，那么由詹森不等式得
\begin{equation}
\frac{1}{2}\left(\log\log(e^x+1) + \log\log(e^{-x}+1)\right)\leq \log\log(e^{(x+(-x))/2}+1)=\log\log 2\end{equation}
也就是$\log\left(\log(e^x+1)\log(e^{-x}+1)\right)\leq 2\log\log 2$，或者$\log(e^x+1)\log(e^{-x}+1)\leq \log^2 2$，两边乘以4即得待证结论。等号成立的条件为$x=-x$，即$x=0$。

至于第二个问题，我们需要有一个“误差”的标准。这里跟之前的文章《GELU的两个初等函数近似是怎么来的》一样，转化为无额外参数的$\min\text{-}\max$问题：
\begin{equation}\min_{b} \max_x \left|\frac{x+\sqrt{x^2+b}}{2} - \log(e^x+1)\right|\end{equation}
这个问题笔者没法求得解析解，目前只能通过数值求解：

import numpy as np
from scipy.special import erf
from scipy.optimize import minimize

def f(x, a):
    return np.abs((x + np.sqrt(x**2 + a**2)) / 2 - np.log(np.exp(x) + 1))

def g(a):
    return np.max([f(x, a) for x in np.arange(-2, 4, 0.0001)])

options = {'xtol': 1e-10, 'ftol': 1e-10, 'maxiter': 100000}
result = minimize(g, 0, method='Powell', options=options)
b = result.x**2
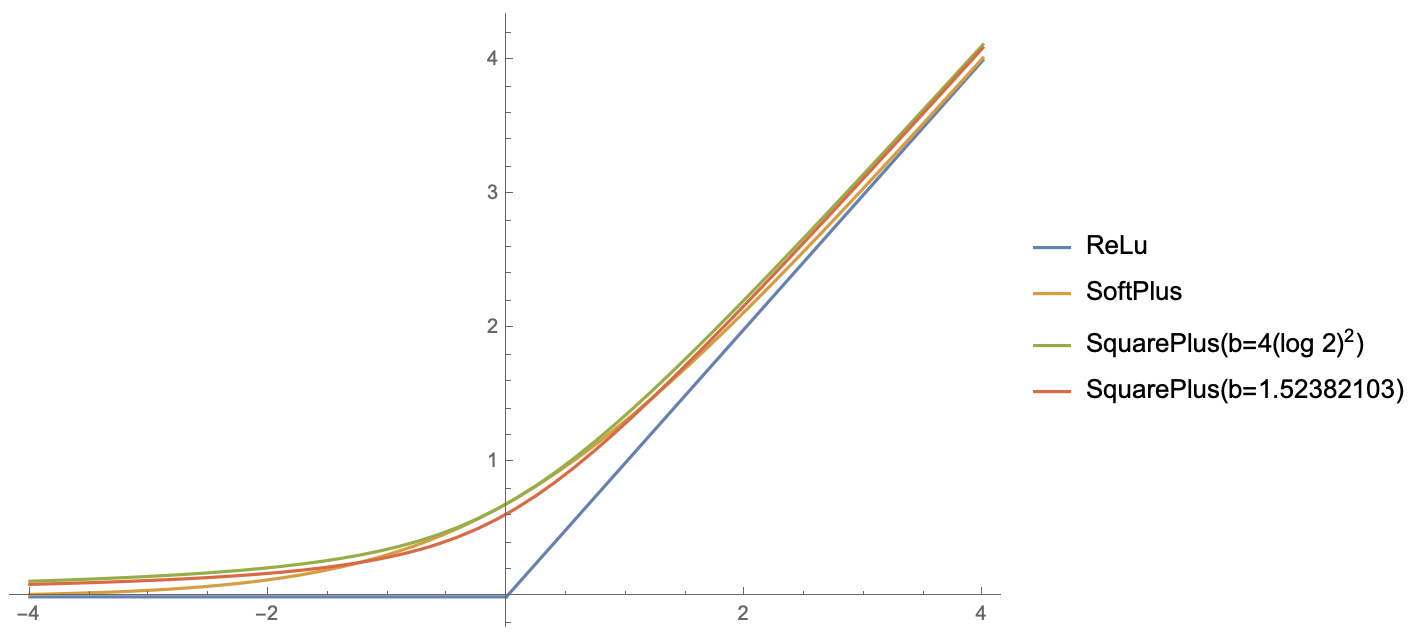
print(b)

最终算出的结果是$b=1.52382103\cdots$，误差最大值为$0.075931\cdots$，比较如下：

小结 #

似乎也没啥好总结的，就是介绍了一个ReLU的光滑近似，并配上了两道简单的函数练习题～

转载到请包括本文地址：https://kexue.fm/archives/8833

更详细的转载事宜请参考：《科学空间FAQ》