等值振荡定理：最优多项式逼近的充要条件

最近在阅读时，遇到了一个关于最优多项式逼近的“等值振荡定理（Equioscillation Theorem）”，证明过程还涉及到无穷范数求导，感觉结论和证明都颇为新奇，特来记录一番。

参考资料：《Notes on how to prove Chebyshev’s equioscillation theorem》和《Approximation Theory – Lecture 5》。

等值振荡 #

我们先展示一下结论：

等值振荡定理 设$f(x)$是不超过$n$阶的多项式，$g(x)$是区间$[a,b]$上的连续函数，那么
\begin{equation}f^* = \mathop{\text{argmin}}_f \max_{x\in[a,b]} |f(x) - g(x)|\end{equation}
的充要条件是存在$a\leq x_0 < x_1 < \cdots < x_{n+1} \leq b$以及$\sigma\in\{0,1\}$，使得
\begin{equation}f^*(x_k) - g(x_k) = (-1)^{k+\sigma} \max_{x\in[a,b]} |f^*(x) - g(x)|\end{equation}

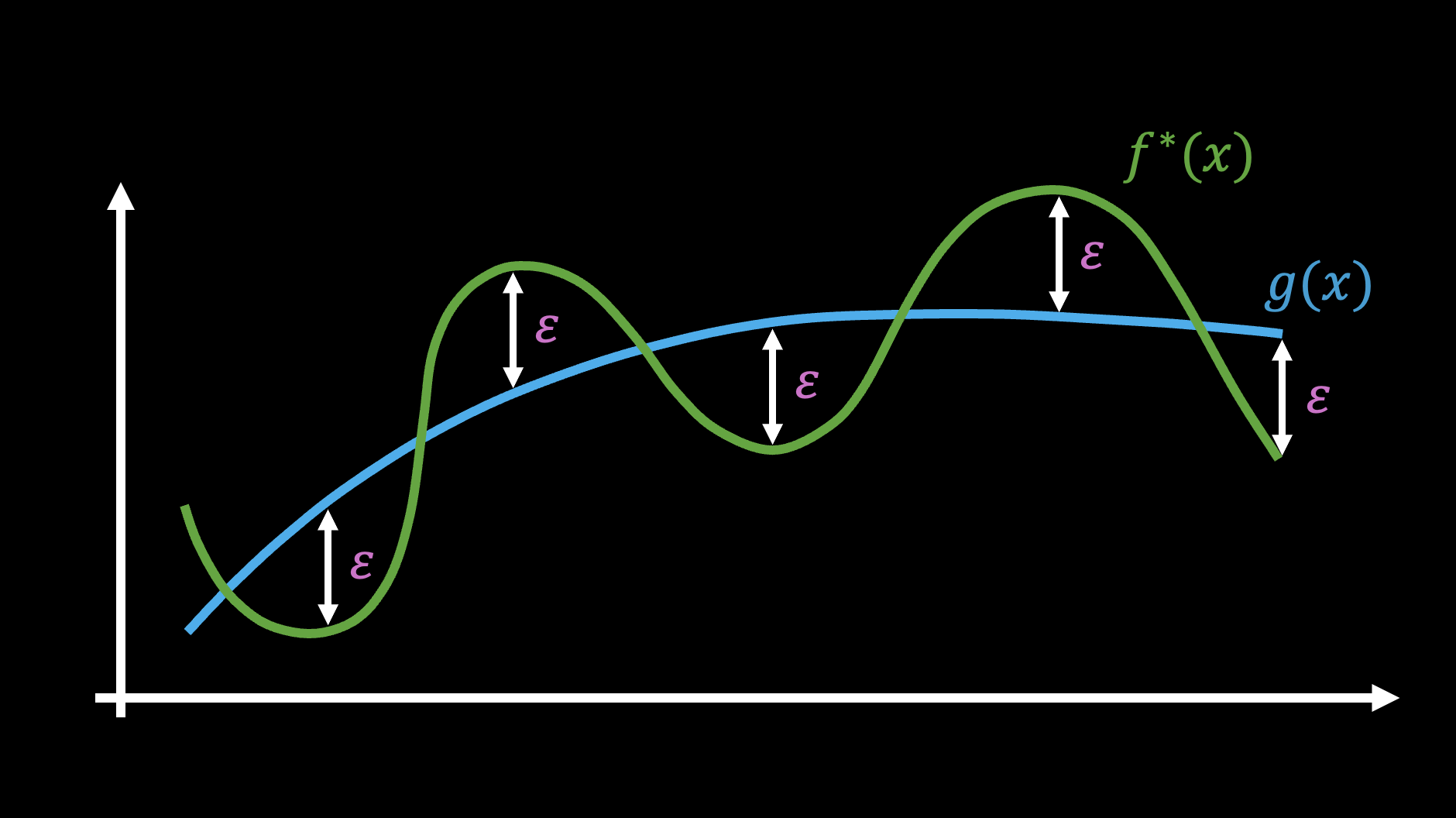
等值振荡定理有时也直接称“Chebyshev定理”，因为它由Chebyshev（切比雪夫）首先发现。虽然定理的文字描述看似复杂，但实际上它有直观的几何意义，如下图所示：

说白了，一个函数的最佳$n$阶多项式逼近，必定交错地穿过原函数，这很符合直觉，而等值振荡定理告诉我们的是“至少$n+2$次交替地重复出现最大误差”，这是非常强的定量信号。

求导思想 #

等值振荡定理所用的误差指标是$\max\limits_{x\in[a,b]} |f(x) - g(x)|$，也就是希望最大的误差尽可能小，它的优点是能自动关注误差最大的地方，并且没有额外的超参数要调。

我们知道，求最值的标准方法就是求导然后让导函数等于零，然而这种带有$\max$的指标求导并不是那么平凡。注意到我们有
\begin{equation}\max_{x\in[a,b]} |f(x) - g(x)| = \lim_{p\to\infty} \left(\int_a^b |f(x)-g(x)|^p\right)^{1/p} = \Vert f(x)-g(x)\Vert_{\infty}\end{equation}
即它是$l_p$范数的无穷版本。如果$p$是一个有限数字，那么求导可以直接按照固定公式进行，但当$p\to\infty$时，可能会出现一些新的变化。这种情况下最稳妥的方式是回归到求导的原始定义：
\begin{equation}\mathcal{D}_x[h(x),u] = \lim_{\epsilon\to 0} \frac{h(x + \epsilon u) - h(x)}{\epsilon}\end{equation}
如果极限存在，并且可以表示成$\langle \varphi(x),u\rangle$的内积形式，那么$\varphi(x)$就是$h(x)$的导数（梯度）。如果$h(x)$在$x$处取到最小值，那么对于足够小的非零$\epsilon$，必然恒成立$h(x + \epsilon u) \geq h(x)$，而对任意$u$恒成立该不等式，那么只能是$\varphi(x)=0$，这就是让导函数等于零找最值的原理。

简单例子 #

我们从一个简单的例子算起，定义$h(x_1,x_2) = \max(x_1,x_2)$，考虑单侧极限
\begin{equation}\mathcal{D}_{x_1,x_2}[h(x_1,x_2),(u_1,u_2)] = \lim_{\epsilon\to 0^+} \frac{\max(x_1 + \epsilon u_1,x_2 + \epsilon u_2) - \max(x_1,x_2)}{\epsilon}\end{equation}

接下来分情况讨论。第一种情况是$x_1 > x_2$，注意我们考虑的是$\epsilon$足够小的极限，所以当$x_1 \neq x_2$时，所加的$\epsilon u_1, \epsilon u_2$是不足以改变排序的，即$x_1 + \epsilon u_1 > x_2 + \epsilon u_2$，所以
\begin{equation}\mathcal{D}_{（x_1,x_2）}[h(x_1,x_2),(u_1,u_2)] = \lim_{\epsilon\to 0^+} \frac{(x_1 + \epsilon u_1) - x_1}{\epsilon} = u_1\end{equation}
同理，$x_1 < x_2$时我们有
\begin{equation}\mathcal{D}_{（x_1,x_2）}[h(x_1,x_2),(u_1,u_2)] = \lim_{\epsilon\to 0^+} \frac{(x_2 + \epsilon u_2) - x_2}{\epsilon} = u_2\end{equation}
最后，当$x_1=x_2$时，我们有$\max(x_1 + \epsilon u_1,x_2 + \epsilon u_2)=x_1 + \epsilon \max(u_1, u_2)$，所以
\begin{equation}\mathcal{D}_{（x_1,x_2）}[h(x_1,x_2),(u_1,u_2)] = \lim_{\epsilon\to 0^+} \frac{(x_1 + \epsilon \max(u_1, u_2)) - x_1}{\epsilon} = \max(u_1,u_2)\end{equation}
可以类似地推广到$\boldsymbol{x}=(x_1,\cdots,x_n),\boldsymbol{u}=(u_1,\cdots,u_n)$，仔细琢磨就可以发现规律是“先找出$\boldsymbol{x}$最大值所在的位置，然后找到$\boldsymbol{u}$对应的最大值”，即
\begin{equation}\mathcal{D}_{\boldsymbol{x}}[\max(\boldsymbol{x}),\boldsymbol{u}] = \lim_{\epsilon\to 0^+} \frac{\max(\boldsymbol{x} + \epsilon \boldsymbol{u}) - \max(\boldsymbol{x})}{\epsilon} = \max_{i\in\mathop{\text{argmax}}(\boldsymbol{x})} u_i\end{equation}
这里不排除$\boldsymbol{x}$的最大值有多个的可能性，所以$\mathop{\text{argmax}}(\boldsymbol{x})$是一个集合。

不难发现，上式无法写成$\langle \boldsymbol{\varphi}(\boldsymbol{x}),\boldsymbol{u}\rangle$的形式，这意味着$\max$算符不存在严格意义上的梯度。当然，两个数严格相等的概率很小，所以如果假设最大值的位置只有一个，那么就可以把梯度分离出来，结果是$\mathop{\text{onehot}}(\mathop{\text{argmax}}(\boldsymbol{x}))$，深度学习框架中的$\max$算子正是这样做的。

加绝对值 #

设$|\boldsymbol{x}|$是给$\boldsymbol{x}$的每个分量都加上绝对值符号后所得的新向量，现在我们考虑$\max(|\boldsymbol{x}|)$的求导，注意到我们有
\begin{equation}\max(|\boldsymbol{x}|) = \max((-\boldsymbol{x}, \boldsymbol{x}))\end{equation}
这里的$(-\boldsymbol{x}, \boldsymbol{x})$代表两个向量拼接成新向量。去掉绝对值后，可以直接代入上一节的结果
\begin{equation}\mathcal{D}_{\boldsymbol{x}}[\max(|\boldsymbol{x}|),\boldsymbol{u}] = \mathcal{D}_{(-\boldsymbol{x},\boldsymbol{x})}[\max((-\boldsymbol{x},\boldsymbol{x})),(-\boldsymbol{u},\boldsymbol{u})] = \max_{i\in\mathop{\text{argmax}}((-\boldsymbol{x},\boldsymbol{x}))} (-\boldsymbol{u},\boldsymbol{u})_i\end{equation}
它还可以再简化一下。注意到$x_i\neq 0$时，$\pm x_i$顶多有一个能成为最大值。如果$x_i$是最大值，那么它必然是正数，并且参与排序的是$u_i$，反之它是负数，参数排序的是$-u_i$，所以我们有
\begin{equation}\mathcal{D}_{\boldsymbol{x}}[\max(|\boldsymbol{x}|),\boldsymbol{u}] = \max_{i\in\mathop{\text{argmax}}((-\boldsymbol{x},\boldsymbol{x}))} (-\boldsymbol{u},\boldsymbol{u})_i = \max_{i\in\mathop{\text{argmax}}(|\boldsymbol{x}|)} \mathop{\text{sign}}(x_i) u_i \end{equation}
也可以写成
\begin{equation}\mathcal{D}_{\boldsymbol{x}}[\Vert\boldsymbol{x}\Vert_{\infty},\boldsymbol{u}] = \max_{i\in\mathop{\text{argmax}}(|\boldsymbol{x}|)} \mathop{\text{sign}}(x_i) u_i \end{equation}
这里成立的前提是$\boldsymbol{x}\neq \boldsymbol{0}$。它可以推广到闭区间上的函数：$\forall f,g\in \mathcal{C}[a,b],f\neq 0$，有
\begin{equation}\mathcal{D}_f[\Vert f\Vert_{\infty},g] = \max_{x\in\mathop{\text{argmax}}(|f(x)|)} \mathop{\text{sign}}(f(x)) g(x) \end{equation}
这就是证明等值振荡定理需要用的关键导数等式。值得指出的是，在这两节的证明过程中，我们实际上只用到了分类讨论而没有用任何近似，所以我们可以找到足够小的阈值$\tau$，使得$\forall \epsilon\in[0,\tau]$，都成立
\begin{equation}\Vert f + \epsilon g\Vert_{\infty} = \Vert f\Vert_{\infty} + \epsilon\, \mathcal{D}_f[\Vert f\Vert_{\infty},g] = \Vert f\Vert_{\infty}
+ \epsilon\max_{x\in\mathop{\text{argmax}}(|f(x)|)} \mathop{\text{sign}}(f(x)) g(x) \label{eq:eps-x}\end{equation}

充要条件 #

这一节正式开始讨论最优逼近。我们先证明一个比多项式逼近更一般的结果，它归功于Kolmogorov（就是KAN的那个K）：

Kolmogorov定理 设$\mathcal{S}\subseteq \mathcal{C}[a,b]$是$\mathcal{C}[a,b]$的一个线性子空间，$f\in \mathcal{S}$且$g\in \mathcal{C}[a,b]$，那么
\begin{equation}f^* = \mathop{\text{argmin}}_f \Vert f - g\Vert_{\infty} = \mathop{\text{argmin}}_f \max_{x\in[a,b]} |f(x) - g(x)|\end{equation}
的充要条件是对任意$h\in \mathcal{S}$，成立
\begin{equation}\mathcal{D}_{f^*}[\Vert f^* - g\Vert_{\infty}, h] = \max_{x\in\mathop{\text{argmax}}(|f^*(x) - g(x)|)} \mathop{\text{sign}}(f^*(x) - g(x)) h(x) \geq 0\label{eq:cond-1}\end{equation}

证明分必要性和充分性两部分，其中必要性直接可以从式$\eqref{eq:eps-x}$和最小值的定义得出，所以我们主要关心充分性。由展开式
\begin{equation}\begin{aligned}
|f(x) - g(x)|^2 =&\, |f(x)-f^*(x)+f^*(x)-g(x)|^2 \\[6pt]
=&\, |f(x)-f^*(x)|^2 + 2(f(x)-f^*(x))(f^*(x)-g(x)) + |f^*(x)-g(x)|^2
\end{aligned}\label{eq:cond-1x}\end{equation}
因为$f,f^*\in \mathcal{S}$，所以$f-f^* \in \mathcal{S}$，设$h=f-f^*$，取$x$为让条件$\eqref{eq:cond-1}$成立的$x$，那么
\begin{equation}(f(x)-f^*(x))(f^*(x)-g(x)) = h(x) \mathop{\text{sign}}(f^*(x)-g(x))|f^*(x)-g(x)| \geq 0\end{equation}
代入式$\eqref{eq:cond-1x}$得$|f(x) - g(x)|^2 \geq |f^*(x)-g(x)|^2$，这意味着$\Vert f-g\Vert_{\infty} \geq \Vert f^* - g\Vert_{\infty}$，所以$f^*$是最优逼近。

定理证明 #

为了完成等值振荡定理的证明，我们选取的子空间$\mathcal{S}$是全体不超过$n$阶的多项式。为了方便大家阅读，这里再重述一下定理内容：

等值振荡定理 设$f(x)$是不超过$n$阶的多项式，$g(x)$是区间$[a,b]$上的连续函数，那么
\begin{equation}f^* = \mathop{\text{argmin}}_f \Vert f(x) - g(x)\Vert_{\infty}= \mathop{\text{argmin}}_f \max_{x\in[a,b]} |f(x) - g(x)|\end{equation}
的充要条件是存在$a\leq x_0 < x_1 < \cdots < x_{n+1} \leq b$以及$\sigma\in\{0,1\}$，使得
\begin{equation}f^*(x_k) - g(x_k) = (-1)^{k+\sigma}\Vert f^*(x) - g(x)\Vert_{\infty} = (-1)^{k+\sigma} \max_{x\in[a,b]} |f^*(x) - g(x)|\label{eq:cond-2}\end{equation}

记$\mathcal{E} = \Vert f^*(x) - g(x)\Vert_{\infty}$，等值振荡定理有三个关键点：1、最大误差$\mathcal{E}$至少出现$n+2$次；2、$\pm \mathcal{E}$刚好是交替出现；3、这构成了最优解的充要条件。

类似地，我们分必要性和充分性来证明。首先我们来看充分性，根据Kolmogorov定理，我们只需要证明满足条件$\eqref{eq:cond-2}$，不可能存在$h\in \mathcal{S}$，使得$\forall x\in\mathop{\text{argmax}}(|f^*(x) - g(x)|)$，都有
\begin{equation}\mathop{\text{sign}}(f^*(x) - g(x)) h(x) < 0\end{equation}
这是因为$\pm \mathcal{E}$交替出现$n+2$次，如果上式成立，那么$h(x)$至少改变了$n+1$次符号，根据介值定理$h(x)$至少有$n+1$个不同的零点，这跟$h\in \mathcal{S}$（$n$次多项式）矛盾。

至于必要性，根据Kolmogorov定理，此时$\forall h\in \mathcal{S}$恒成立
\begin{equation}\max_{x\in\mathop{\text{argmax}}(|f^*(x) - g(x)|)} \mathop{\text{sign}}(f^*(x) - g(x)) h(x) \geq 0\label{eq:cond-3}\end{equation}
我们先将$\mathop{\text{argmax}}(|f^*(x) - g(x)|)$的元素从小到大排序，然后将让$f^*(x) - g(x)$符号相同的相邻元素合并在一组，那么必要性就是说我们至少能分出$n+2$组。假设只能分$m \leq n + 1$组，那么我们可以给这$m$组找到$m-1$个分隔点$z_1 < z_2 < \cdots < z_{m-1}$，这样一来我们考虑
\begin{equation}h_{\pm}(x) = \pm (x-z_1)(x-z_2)\cdots (x - x_{m-1})\in \mathcal{S}\end{equation}
$h_{\pm}(x)$至少有一个，它跟$f^*(x) - g(x)$总是异号的（$\forall x \in \mathop{\text{argmax}}(|f^*(x) - g(x)|)$），不妨设是$h_+(x)$，那么
\begin{equation} \mathop{\text{sign}}(f^*(x) - g(x)) h_+(x) < 0,\qquad \forall x\in\mathop{\text{argmax}}(|f^*(x) - g(x)|)\end{equation}
这就跟$\eqref{eq:cond-3}$矛盾。所以$m > n+1$，即$\mathop{\text{argmax}}(|f^*(x) - g(x)|)$元素至少有$n+2$个，相应的$f^*(x) - g(x)$符号至少改变$n+1$次。

唯一最优 #

一个自然的问题是，等值振荡定理里边的最优多项式逼近是唯一的吗？答案是肯定的。这个证明也比较巧妙，参考了笔记《Chebyshev Equioscillation Theorem》。

假设$f_1^*, f_2^*$是$g$的两个最优多项式，我们先证明$(f_1^* + f_2^*)/2$也是最优逼近：
\begin{equation}\left\Vert \frac{f_1^* + f_2^*}{2} - g\right\Vert_{\infty} = \left\Vert \frac{f_1^* - g}{2} + \frac{f_2^* - g}{2}\right\Vert_{\infty}\leq \frac{1}{2}\Vert f_1^* - g\Vert_{\infty} + \frac{1}{2}\Vert f_2^* - g\Vert_{\infty} = \mathcal{E} \end{equation}
最后的等号是因为$f_1^*, f_2^*$都是最优逼近，所以$\Vert f_1^* - g\Vert_{\infty} = \Vert f_2^* - g\Vert_{\infty} = \mathcal{E}$。由于$(f_1^* + f_2^*)/2$的最大误差也不超过$\mathcal{E}$，所以它也是最优逼近。

那么根据等值振荡定理，至少存在$n+2$个不同的$x$，使得
\begin{equation}\frac{f_1^*(x) + f_2^*(x)}{2} - g(x) = \pm\mathcal{E} \end{equation}
又因为
\begin{equation}\frac{f_1^* + f_2^*}{2} - g = \frac{f_1^* - g}{2} + \frac{f_2^* - g}{2}\end{equation}
且$f_1^*(x) - g(x),f_2^*(x) - g(x)\in[-\mathcal{E},\mathcal{E}]$，所以$f_1^*(x) - g(x),f_2^*(x) - g(x)$只能同号且都等于$\mathcal{E}$或$-\mathcal{E}$。这意味着多项式$f_1^*-f_2^*$至少有$n+2$个零点，但$f_1^*-f_2^*$是一个$n$次多项式，它有$n+2$个零点意味着它只能恒等于零，即$f_1^*=f_2^*$。

两个变体 #

最后，我们给出等值振荡定理在奇多项式/偶多项式上的变体。奇多项式/偶多项式是指只含有奇数次幂/偶数次幂的多项式，比如$x + 2x^3$和$1 + 4x^2 + x^4$，它们的特点是零点必然正负成对出现，所以一个不超过$2n+1$阶的奇多项式/偶多项式，在$(0,\infty)$上至多有$n$个零点。

对于奇多项式/偶多项式，我们有

等值振荡定理-奇/偶 设$f(x)$是不超过$2n+1$阶的奇多项式/偶多项式，$g(x)$是区间$[a,b]\subset (0,\infty)$上的连续函数，那么
\begin{equation}f^* = \mathop{\text{argmin}}_f \Vert f(x) - g(x)\Vert_{\infty}= \mathop{\text{argmin}}_f \max_{x\in[a,b]} |f(x) - g(x)|\end{equation}
的充要条件是存在$a\leq x_0 < x_1 < \cdots < x_{n+1} \leq b$以及$\sigma\in\{0,1\}$，使得
\begin{equation}f^*(x_k) - g(x_k) = (-1)^{k+\sigma}\Vert f^*(x) - g(x)\Vert_{\infty} = (-1)^{k+\sigma} \max_{x\in[a,b]} |f^*(x) - g(x)|\end{equation}

证明步骤跟一般的等值振荡定理基本相同，只需要稍微调整一下细节，请有兴趣的读者自行完成。

文章小结 #

本文介绍了多项式最优逼近的等值振荡定理（Equioscillation Theorem），以及与之相关的无穷范数求导问题。

转载到请包括本文地址：https://kexue.fm/archives/10972

更详细的转载事宜请参考：《科学空间FAQ》