旋转的弹簧将如何伸长?
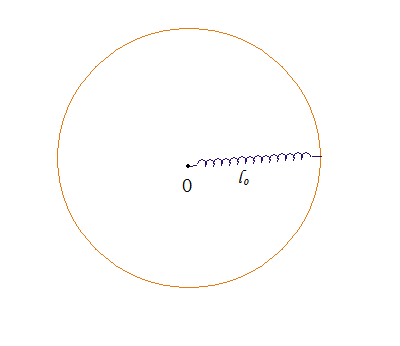
By 苏剑林 | 2010-07-30 | 122441位读者 |一根均匀的弹簧长度l0,线密度λ
0,劲度系数k,总质量M。现在没有重力的环境下,绕其一端作角速度ω的旋转(角速度恒定),则此时其长度变为多少?
这是网友“宇宙为家”在几天前提出的问题。期间我曾做过多次解答,犯了若干次错误,经过修修补补,得出了最后的答案,在此感谢“宇宙为家”朋友的多次提醒。如果下面的答案依旧有错误,望各位读者发现并指出。
首先要把题目理解清楚,弹簧在旋转前是均匀的,但是旋转后由于不同点受到的“惯性离心力”不同,所以每一部分弹簧必将不均匀地伸长,导致密度不再是常数。由于弹簧变得不均匀,因此以“长度比”来衡量劲度系数比已经不可靠了,应该以“质量比”来表达。设在旋转之后密度函数为$\lambda=\lambda(r)$,r是弹簧上的一个横断面到旋转重心O的距离,弹簧上每一点的惯性离心力为$dF_c=r\omega^2 dm=\lambda r\omega^2 dr$,那么距离圆心为r处的弹簧的断面受到的惯性离心力为$F_c=\int_r^{l}\lambda r\omega^2 dr$(注:$F_c$即Centrifugal force,离心力,这是为了避免与下面的F混淆)。每一段长度为dr弹簧的劲度系数为$\frac{M}{dm}k$,由于惯性离心力的作用,伸长量为$\frac{\int_r^{l}\lambda r\omega^2 dr}{Mk/dm}=\frac{\omega^2 dm}{Mk}\int_r^{l}\lambda r dr$,旋转前这一段的长度为$\frac{dm}{\lambda_0}$,显然这一段的密度为$\lambda=\frac{dm}{\frac{dm}{\lambda_0}+\frac{\omega^2 dm}{Mk}\int_r^{l}\lambda r dr}=\frac{1}{\frac{1}{\lambda_0}+\frac{\omega^2}{Mk}\int_r^{l}\lambda r dr}$
请看最后一步,我们已经是列出了关于密度函数的“积分方程”:
$$\lambda=\frac{1}{\frac{1}{\lambda_0}+\frac{\omega^2}{Mk}\int_r^{l}\lambda r dr}$$
这是BoJone解答这道题目的关键。对于BoJone来说,解积分方程是很困难的,通过变换,可以将其变为微分方程(其实对BoJone而言,解微分方程也不容易)。
设$F=\int_r^{l}\lambda r dr$,则$\lambda =-\frac{dF}{rdr}=-\frac{\dot{F}}{r}$,代入原来的方程,得到:
$$\begin{aligned}-\frac{\dot{F}}{r}=\frac{1}{\frac{1}{\lambda_0}+\frac{\omega^2}{Mk}F} \\ -r=\frac{\dot{F}}{\lambda_0}+\frac{\omega^2}{Mk}F\dot{F}\end{aligned}$$
这道微分方程显得如此简单,积分一次就得到:
$$C-\frac{1}{2} r^2=\frac{F}{\lambda_0}+\frac{\omega^2}{2Mk}F^2$$
C是积分常数,根据F的定义,可以得出当r=l时,应该有F=0,所以推出:$C=\frac{1}{2} l^2$,并且从中解出F,得到
$$F=\pm \sqrt{\frac{Mk}{\omega^2}(l^2-r^2)+(\frac{Mk}{\omega^2\lambda_0})^2}-\frac{Mk}{\omega^2\lambda_0}$$
舍去负值(自己想原因?)
可以计算
$$\lambda =-\frac{dF}{rdr}=\frac{Mk}{\omega^2\sqrt{\frac{M^2 k^2}{\omega^4 \lambda_0^2}+\frac{Mk (l^2-r^2) }{\omega^2}}}=\frac{1}{\sqrt{\frac{1}{\lambda_0^2}+\frac{\omega^2(l^2-r^2)}{Mk}}}$$
根据密度函数的定义,应该有
$$\int_0^l \lambda dr=\int_0^l \frac{dr}{\sqrt{\frac{1}{\lambda_0^2}+\frac{\omega^2(l^2-r^2)}{Mk}}}=M$$
这个积分的结果是
$$\frac{\sqrt{Mk}}{\omega}arcsin( \frac{r\omega}{\sqrt{l^2\omega^2+\frac{Mk}{\lambda_0^2}}})$$
于是我们有
$$M=\frac{\sqrt{Mk}}{\omega}arcsin( \frac{l\omega}{\sqrt{l^2\omega^2+\frac{Mk}{\lambda_0^2}}})$$
为了方便计算,根据$arcsin(\frac{a}{b})=arctg\frac{a}{\sqrt{b^2-a^2}}$,可以将上式变成
$$M=\frac{\sqrt{Mk}}{\omega}arctg(\frac{l\omega\lambda_0}{\sqrt{Mk}})$$
可以解出
$$l=\frac{\sqrt{Mk}}{\lambda_0 \omega}tg(\omega\sqrt{M/k})=l_0\cdot \frac{1}{\omega}\sqrt{k/M}tg(\omega\sqrt{M/k})$$
这个答案很漂亮!首先$\frac{1}{\omega}\sqrt{k/M}$和$\omega\sqrt{M/k})$互为倒数,这两个具有对称的美。而且M的量纲是$M$,k的量纲是$\frac{M}{T^2}$,那么$\sqrt{M/k}$的量纲就是$T$,而$\omega$的量纲是$1/T$,那么$\frac{1}{\omega}\sqrt{k/M}$和$\omega\sqrt{M/k})$均是无量纲的量,这与答案的运算过程是自洽的!再者,当$\omega\sqrt{M/k}->\pi/2$时,$l->\infty$,换句话说,$\omega\sqrt{M/k}$不能超过$\pi/2$,这给出了衡量弹簧性能的一个参数:$\omega=\pi/2 \sqrt{k/M}$,如果$\omega$越大,那么就说明弹簧“受折腾”能力越强,也就是性能越好!
转载到请包括本文地址:https://kexue.fm/archives/782
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 30, 2010). 《旋转的弹簧将如何伸长? 》[Blog post]. Retrieved from https://kexue.fm/archives/782
@online{kexuefm-782,
title={旋转的弹簧将如何伸长? },
author={苏剑林},
year={2010},
month={Jul},
url={\url{https://kexue.fm/archives/782}},
}










July 30th, 2010
我看懂了,自己算了一遍。不过最后的答案很诡异,omega是任意的,不能对它有什么限制,那岂不可以无限长或是负数了。诡异诡异
如果我的结果是正确的,那么omega就不能任意大。或许$\omega=\pi/2 \sqrt{k/M}$是衡量弹簧性能的一个参数,$\omega$越大,那么就说明弹簧“受折腾”能力越强,也就是性能越好!
July 30th, 2010
问题是$\omega\sqrt{M/k}$如果等于$\pi/2$呢?这是绝对可能的,如果大于$\pi/2$小于$pi$呢?这都是完全可能的啊,你说呢
你试验过了吗?
你说的试验是什么意思
按你的说法,给定一个弹簧,它的角速度不能超过$\pi/2\sqrt{k/M}$而且当角速度接近$\pi/2\sqrt{k/M}$时,弹簧无限长。力没有无限大弹簧怎会无限长呢?常理告诉我们$\omega$越大,弹簧越长。虽然常识也许是错的,但这个答案更荒谬
我说的试验指的是在实验中验证一下这道题目是否符合我的公式。
按照我的计算结果,角速度达到$\pi/2 sqrt{k/M}$时,力已经是无穷大了(或者说要维持这个角速度需要无穷大的向心力)。
不能着重于常理,更加不能着重于计算过程,你仔细想想,维持角速度一定,弹簧会由静止长度伸长,伸长后由于角速度不变,长度变了,必然导致力再次发生变化,这样一直下去达到平衡...
那$\omega$如果超过$\pi/2\sqrt{k/M}$呢
我不知道,或许弹簧会一直加速伸长下去,直到断裂(如果不断裂那么就是无限长)。
July 30th, 2010
还有$\lambda=-frac{dF}{rdr}$为什么加个负号啊
注意F是一个定积分,r是积分的下界,也就是说F=F(l)-F(r)
August 3rd, 2010
弹簧上每一个质量元会同时受到来自两侧的弹力,上面的式子计算离心力时似乎没有考虑向外的弹力。
可以这样类比:用F力拉着固定在墙上的弹簧,弹簧同样受到墙对弹簧有F的拉力,但是弹簧的伸长量是F/k而不是2F/k
March 5th, 2011
hey,find wow gold click here
January 3rd, 2012
若弹簧为压缩弹簧呢?外圆为固定端,以角速度ω旋转,会缩短多少呢?
答案应该是类似的,我用我的第一种方法算了一下,我好像算得$l=r[1-cos(\sqrt{\frac{M}{k}}\omega)+sin(\sqrt{\frac{M}{k}}\omega)*\sqrt{\frac{kl_0^2}{Mr^2\omega^2}-1} .]$,不知道正确与否,还没有时间检验。
August 24th, 2012
从r积分到l,这个r有点错误吧?前面一段也被拉伸了,就不该是r了。
可是这个r已经是拉伸后的长度函数了。
给个E-mail,交流下,我把你的文档整理了下,发给你
好呀,欢迎交流。^_^
邮箱在头顶的"关于本站"...
bojone@spaces.ac.cn
October 18th, 2013
如果考虑重力场的影响呢?
如果圆面与重力平行,那么重力与离心力的方向处处不相同,显然不能达到平衡状态的(或者说重力势能处处不等,所以无法达到平衡)。如果圆面与重力垂直,可以达到平衡状态,但是这涉及到弹簧的非线性弯曲了~这方面还没有研究过呢。
August 18th, 2014
答案应该没有错,我也算出来一样结果了,用到的方法很奇特,将弹簧当成皮筋,假想皮筋的“横截面积”与拉力的关系。然后一个关于皮筋各个位置拉力的微分方程,加初值解出了横截面积的函数。过程中字母都一大堆的,不过都是软件计算,没想到结果会如此简单。这题还可以弹簧一头连接个重物,估计结果会复杂点
本身的解答过程也不算特别复杂,那是我以前做的题目了,基本上都是手算,因为那时候对软件也不熟悉。连接个重物之后,大概长一点,但也没有难度上的差异了。毕竟,微元法就相当于已经把弹簧看成无限个小重物了。
May 5th, 2019
你这里面距离圆心为r处的弹簧的断面受到的惯性离心力和长度为dr弹簧两个dr感觉意义不同