函数图像旋转公式(“想当然”的教训)
By 苏剑林 | 2010-02-09 | 141845位读者 |阅读小提示:亲爱的读者,你可以选择不读这篇文章,但如果你选择了阅读,请一定要阅读完。BoJone对“半途而废”所造成的后果一概不负责任^_^。
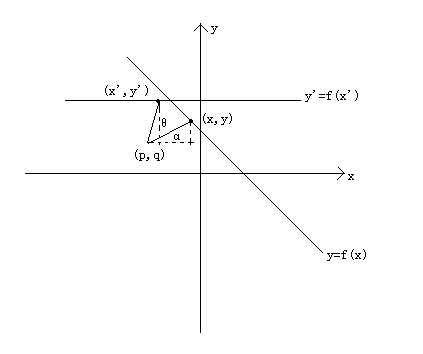
我们来考虑下一个旋转问题:将某一函数图像y=f(x),绕点(p,q)逆时针旋转了θ角之后,得到的图象的解析式。
首先,由于仅仅是通过了旋转,所以函数的整体图像并没有变化,因此一定也是原来的函数f,我们在原来的函数图像上随便选取一点(x,y),对应在旋转后的图像为(x’,y’),那么新的图像解析式应该是y’=f(x’).而且由于图像是绕(p,q)旋转的,所以(x,y)和(x’,y’) 两个点到(p,q)的距离应该相等,设这个距离为r,即$\sqrt{(x-p)^2+(y-q)^2}=r$;令(x,y)-(p,q)(这是指两个点之间的连线,下同)与x轴的“过(p,q)的平行线”所成的角为α,于是我们有:
$\sin\alpha=\frac{y-q}{r}$,$\cos\alpha=\frac{x-p}{r}$
继而:
$$\begin{aligned}\sin(\alpha +\theta)=\sin\alpha \cos\theta+\sin\theta \cos\alpha= \frac{y-q}{r} \cos\theta+\frac{x-p}{r}\sin\theta \\ \cos(\alpha +\theta)=\cos\alpha \cos\theta-\sin\theta \sin\alpha= \frac{x-p}{r} \cos\theta-\frac{y-q}{r}\sin\theta\end{aligned}$$
于是很显然:
$$\begin{aligned}y' =(\frac{y-q}{r} \cos\theta+\frac{x-p}{r}\sin\theta)r+q=(y-q)\cos\theta+(x-p)\sin\theta+q \\ x' =(\frac{x-p}{r} \cos\theta-\frac{y-q}{r}\sin\theta)r+p=(x-p)\cos\theta-(y-q)\sin\theta+p\end{aligned}$$
到此,问题解决了,新函数的解析式为:
$$(y-q)\cos\theta+(x-p)\sin\theta+q=f[(x-p)\cos\theta-(y-q)\sin\theta+p]$$
特别地,绕原点旋转的方程为:
$$y \cos\theta+x \sin\theta=f(x \cos\theta-y \sin\theta)$$
例如:y=6-x,绕(0,0)逆时针旋转45°后,结果为
$$\begin{aligned}\frac{\sqrt{2}}{2}(x+y)=6-[\frac{\sqrt{2}}{2}(x-y)] \\ x=3\sqrt{2}\end{aligned}$$
注意,问题来了!明明是$y=3\sqrt{2}$,怎么变成了…?哈哈,大家和我一样,掉进了“陷阱”了!再仔细推敲,发现似乎有点问题;再推一下,又好像没有呀。难道…?其实,问题在一开始的时候就出现了!
一开始我们就设新图像的函数是f(注意划线),这是毫无根据的、而且是错误的。我们已经知道了原来图像中的函数为y=f(x),然后可以确定(x,y)与(x’,y’)之间的关系,求的是x’与y’之间的关系。正确的做法是:分别求出x、y关于x’、y’的表达式,然后代入y=f(x),结果就是x’与y’的关系了!原来的思考过程是没有错误的,只要修改一下原来的过程,就可以得出答案了:
设β=α+θ,有
$$\begin{aligned}\sin(\beta-\theta)=\sin\beta \cos\theta-\sin\theta \cos\beta= \frac{y'-q}{r} \cos\theta-\frac{x'-p}{r}\sin\theta \\ \cos(\beta -\theta)=\cos\beta \cos\theta+\sin\theta \sin\beta= \frac{x'-p}{r} \cos\theta+\frac{y'-q}{r}\sin\theta\end{aligned}$$
于是很显然:
$$\begin{aligned}y =(\frac{y'-q}{r} \cos\theta-\frac{x'-p}{r}\sin\theta)r+q=(y'-q)\cos\theta-(x'-p)\sin\theta+q \\ x =(\frac{x'-p}{r} \cos\theta+\frac{y'-q}{r}\sin\theta)r+p=(x'-p)\cos\theta+(y'-q)\sin\theta+p\end{aligned}$$
代入y=f(x),就有
到此,我们终于得出了新函数的解析式(逆时针):
$$(y-q)\cos\theta-(x-p)\sin\theta+q=f[(x-p)\cos\theta+(y-q)\sin\theta+p]$$
要是顺时针旋转的话:
$$(y-q)\cos\theta+(x-p)\sin\theta+q=f[(x-p)\cos\theta-(y-q)\sin\theta+p]$$
特别地,绕原点旋转的方程为:
$y cos\theta-x sin\theta=f(x cos\theta+y sin\theta)$(逆时针)
$y cos\theta+x sin\theta=f(x cos\theta-y sin\theta)$(顺时针)
这一次没有错误了吧?y=6-x,绕(0,0)逆时针旋转45°后,结果为
$$\begin{aligned}\frac{\sqrt{2}}{2}(y-x)=6-[\frac{\sqrt{2}}{2}(x+y)] \\ y=3\sqrt{2}\end{aligned}$$
费了一番周折,答案终于出来……
感悟:
这时候读者明白我为什么要强调读完这篇文章的缘故了吧?并不是这篇文章特别地重要,只是如果一旦读到一半,就把公式或者方法抄了去,以后用的时候发现总是出错,那时候就不好了^_^。
为什么我一开始要把读者们都引入一个“陷阱”呢?其实我相信这样的错误很多人都犯过,这篇文章描述了BoJone对这个问题的整个思考过程,从思考、错误到修正错误,错误的根源在于“想当然”、“应该是”之类的想法。要是无法冲破这个牢笼,就难以在数学、物理领域前进。这篇文章既是让自己引以为鉴,也希望读者们不要“覆前人之车”。记住:数理没有想当然!
转载到请包括本文地址:https://kexue.fm/archives/416
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Feb. 09, 2010). 《函数图像旋转公式(“想当然”的教训) 》[Blog post]. Retrieved from https://kexue.fm/archives/416
@online{kexuefm-416,
title={函数图像旋转公式(“想当然”的教训)},
author={苏剑林},
year={2010},
month={Feb},
url={\url{https://kexue.fm/archives/416}},
}










February 18th, 2010
没有看完全文。
一看到“首先,由于仅仅是通过了旋转,所以函数的整体图像并没有变化,因此一定也是原来的函数f”这句我就马上感觉到这是不对的。除非特例,一个函数经过旋转之后,肯定不是原来的函数。比如一根直线,旋转后,其解析式就不同了。
之所以有文章开头划线部分的想法,大概是人的参照系跟着函数旋转而已。比如任一几个图形,它旋转后形状是不变,但其解析式(基于特定的坐标系)是变化的。而图形的形状是跟参照系无关的。或者这么说,一个图形,经过任意的转动之后,我们可以找到一个坐标系,在这个新坐标系中,图形的解析式跟未转动前它以原来的坐标系为参考所得的解析式一样。
这是一个“潜意识”的问题,我们在处理平移时,都是在原函数基础上对x,y进行加减处理的,所以很容易一下子就把这个理念用到了旋转上。我刚开始也是这样,后来才处理好。
一开始的时候我越做越怀疑,因为感觉找不到论据,直到用实例验证,才发现错误。后来经过修改,数理关系立即严明了,做起来会舒服很多。也许这就是数学爱好者的一种直觉吧。这也说明了验算多么重要。
August 23rd, 2010
哇哇哇,受益颇多
November 12th, 2010
用极坐标证明简单多了
写这篇文章的时候,还不怎么了解极坐标,特别是那时数学基础还不牢
August 4th, 2015
其实第二部你导出正确结论,只需要在第一部中,解出,x,y.
实质犯的错误是代入错误(小错误)。
August 20th, 2020
有问题请教,有空吗?
有问题请直接留言提问,不需要问是否有空
多谢苏老师回应。上传不了图片,麻烦苏老师移步至我发在贴吧的帖子tieba.baidu.com/p/6890649012。问的是曲线的方程式,麻烦了。
问题看到了,但是我没看懂你那几条虚线是按什么规则画出来的,是不是要说明一下?
等价于一个点A在圆周上匀速运动,点B从圆心出发以A的0.8倍速度一直朝向A运动,求B的轨迹。
那其实就是一个追踪问题了,跟 https://kexue.fm/archives/1047 差不多,只不过被追踪的轨迹变成了一个圆。
设圆周运动的轨迹为$(\cos t, \sin t)$,待求轨迹为$(x(t),y(t))$,那么可以列出微分方程
$$\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2=u^2,\quad \frac{dy}{dx}=\frac{\sin t - y}{\cos t - x}$$
得到
$$\left\{\begin{aligned}&\frac{dx}{dt}=\frac{(\cos t - x)u}{\sqrt{(\cos t - x)^2 + (\sin t - y)^2}}\\
&\frac{dy}{dt}=\frac{(\sin t - y)u}{\sqrt{(\cos t - x)^2 + (\sin t - y)^2}}\end{aligned}\right.$$
除了数值解我也想不到什么办法了~
感谢老师讲解!
老师,如何判断微分方程有没有解析解?比如以下的方程:{{∂y}\over{∂x}}={{k-sin(x)}\over{{{cos^2(x)+k*sin(x)}\over{L}}-{{cos(x)}\over{y}}}}
@意|comment-14293
我也不清楚
老师,如何求得这方程的近似解析解?麻烦您了!!
@意|comment-14300
不知道呀
September 23rd, 2020
老师,“那其实就是一个追踪问题了,跟 https://kexue.fm/archives/1047 差不多,”这里面最后一条式的s(t)一阶是什么来的?
哪里有s(t)?
“有兴趣的朋友可以自己推算,这里贴出BoJone的计算结果:
〈这里的式〉
上式是关于 和 的二阶微分方程。
(感谢上海交通大学数学系 ,这里提供上海交大的”
这段文字中间那里的式。
已经补充说明了,感谢指出。
老师,这个二阶微分方程怎么解呢?我算了两天都没算出来。
不知道。
老师,https://tieba.baidu.com/p/7148286856 这类微分方程怎么解?
October 23rd, 2020
老师,LaTeX怎么输入朗伯函数?
谢谢!
你说的“朗伯函数”是哪个?有没有图?我搜到的记号就是用W来表示。
是跟sin,cos之类的,直接写字母w吗?
维基百科都是直接用$W$。
多谢老师