你见过正方形轮子的自行车吗?一般认为,只有圆形的车轮才能使我们的车子平稳向前移动,但这只是针对平直道路而言的。谁规定路一定是平的?只要铺好一条适当的道路,正方形车轮的自行车照样可以平稳前行!本文就让我们为方轮自行车铺一条路。
其实,方轮自行车已经不是新鲜玩意了,它早已出现在不少科技馆中。从图片中可以看到,它的特殊轨道是有许多段弧组成的,每一段弧的长度等于正方形的边长。车轮前行时,正方形会保持与弧形相切(确保不会打滑)。这样的路的形状是什么曲线呢?很幸运,它并不十分复杂,而且让人意外的是,它就是我们之前已经研究过的“悬链线”!原来,要设计这样的一个曲线的轨道,不需要多么高深的设计师,只需要我们手拿一条铁链,让它自由垂下......
混沌的世界——“星之轨迹”的研究
By 苏剑林 | 2012-01-13 | 49004位读者 | 引用(本文已被刊登在2012年1月的《天文爱好者》上,于笔者而言这是一份很棒的新年礼物!)
在去年第七期《天爱》上,我们看到了N体问题所呈现出来的一些对称、漂亮的周期轨道,这体现了N体问题和谐有序的一面。但是这仅仅是N体问题的冰山一角,笔者也提到过N体问题的本质是混沌、无序的,通俗来讲就是非常乱,无法用数学方程来精确描述。这看起来是一种不完美。但试想,探索当初伽利略将望远镜对准月球后,看到的是如想象中光滑的月面,那么他还会惊叹宇宙的神奇吗?
本文就让我们来更深入地了解一下N体问题的研究历史。
观测&拟合时代
由于人类的自我优越感以及日月星辰东升西落的经验,让我们长期都认为地球是宇宙的中心。第一个比较系统提出地心说的人当属天文学家欧多克斯(Eudoxus,死于公元前347年左右),但他的地心说是非常粗糙的,以至于无法解释很多基本现象,如无法准确预言日食和解释行星逆行等。但亚里士多德接受了地心说,并且由于他在政治和科学上的权威,使地心说免去了夭折的命运。后来托勒密通过他的本轮,完善了地心说,使之延续到了16世纪。
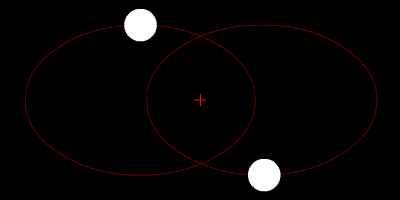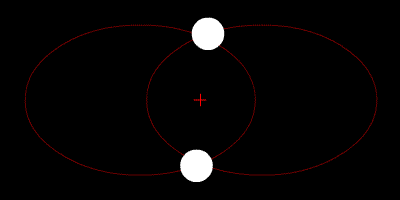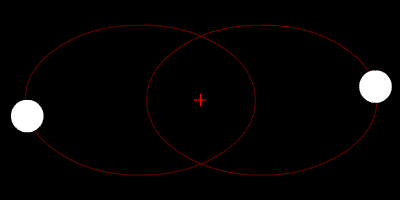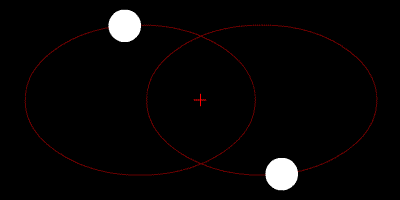
我们在研究地球附近的小天体运动时,如果把天体和地球看作一个二体系统,那最多只能算上一个零级近似,如果使用“地球+月球+小天体”组成的圆形限制性三体问题模型,那可以算上一个二级近似了。那么,一级近似又是什么了。BoJone认为,它就是本文将要讲的“双固定引力中心问题”了,也叫“双不动中心问题”,英文名是two fixed-center problem。这是一种特殊的限制性三体问题。在这个三体系统中,两个主天体(或称有限质量天体)固定不动,第三个小天体在两个固定的主天体吸引下运动。欧拉、拉格朗日、勒让德、雅可比等人很早就研究过这个问题。其中,欧拉最先成功地求出了这个系统的积分。[引用]
另外,双固定引力中心问题还有另外一个应用,在研究人造卫星的运动时,可以只考虑地球引力,但是由于地球不是完美的球体,把其看成一个质点其实不十分精确,要是把它拆分为两个引力源,就可以很大程度上提高精确度。毕竟双固定引力中心问题是完全可以积分的,可以作为一个比较好的中间轨道(介乎圆锥曲线和精确轨道之间的)。
《方程与宇宙》:限制性三体的那些事儿(八)
By 苏剑林 | 2011-02-04 | 34010位读者 | 引用在上一些关于限制性三体问题的探讨中,我们得出了在平面上的方程:
$$\ddot{R}+2i\omega \dot{R}=\omega^2 R-GM\frac{R-l_1}{|R-l_1|^3}-Gm\frac{R-l_2}{|R-l_2|^3}\tag{32}$$
能量积分为:
$$\frac{1}{2}|\dot{R}|^2=\frac{1}{2} \omega^2 |R|^2+\frac{GM}{|R-l_1|}+\frac{Gm}{|R-l_2|}-C\tag{33}$$
下面就以这两个方程为基础,再说说限制性三体问题的那些事儿...
唠叨下,关于三体问题周期轨道
By 苏剑林 | 2011-01-26 | 39089位读者 | 引用《方程与宇宙》:抛物线与双曲线轨道(三)
By 苏剑林 | 2010-04-03 | 64057位读者 | 引用《方程与宇宙》:二体问题的来来去去(一)
By 苏剑林 | 2010-03-20 | 121615位读者 | 引用为了让大家能够查询到“天体力学”方面的内容,同时锻炼我的表达和计算能力,BoJone构思了《方程与宇宙》这个主题,主要是写一些关于使用数学相对深入地讨论一些天文问题。其实我一直觉得,不用公式是无法完美地描述科学的(当然也不能纯公式),我记得霍金的《时间简史》以及《果壳中的宇宙》等之类的书,都力求不用或者尽可能少用数学公式来表达自己的观点。这种模式对于对于公众来说是很好的,但是对于希望深入研究的朋友来说却难以进行。所以我主张:宇宙是算出来的!
这个主题每一个字都是由BoJone敲击出来的,其中包括引用了《天体力学引论》里面的一些内容,以及加入了BoJone个人的一些见解。由于篇幅长及时间有限问题,BoJone打算分若干次撰写发布,并且尽可能写得通俗一点,力求让有一点微积分基础的朋友就可以弄懂。这里首先发布第一部分。由于时间匆忙等原因,可能会出现一些疏忽,欢迎大家挑错!










最近评论