科学空间|Scientific Spaces

陆陆续续写了几篇最小熵原理的博客，致力于无监督做NLP的一些基础工作。为了方便大家实验，把文章中涉及到的一些算法封装为一个库，供有需要的读者测试使用。

由于面向的是无监督NLP场景，而且基本都是NLP任务的基础工作，因此命名为nlp zero。

地址

Github: https://github.com/bojone/nlp-zero
Pypi: https://pypi.org/project/nlp-zero/

可以直接通过

pip install nlp-zero==0.1.6

进行安装。整个库纯Python实现，没有第三方调用，支持Python2.x和3.x。

点击阅读全文...

在前一文《最小熵原理（二）：“当机立断”之词库构建》中，我们以最小熵原理为出发点进行了一系列的数学推导，最终得到$(2.15)$和$(2.17)$式，它告诉我们两个互信息比较大的元素我们应该将它们合并起来，这有利于降低“学习难度”。于是利用这一原理，我们通过邻字互信息来实现了词库的无监督生成。

由字到词、由词到词组，考察的是相邻的元素能不能合并成一个好“套路”。可是套路为什么非得要相邻的呢？当然不一定相邻，我们学习语言的时候，不仅仅会学习到词语、词组，还要学习到“固定搭配”，也就是说词语怎么运用才是合理的，这是语法的体现，是本文所要探究的，希望最终能达到一定的无监督句法分析的效果。

由于这次我们考虑的是跨邻词的语言关联，因此我给它起个名字为“飞象过河”，正是

“套路宝典”第二式——“飞象过河”

语言结构

对于大多数人来说，并不会真正知道什么是语法，他们脑海里就只有一些“固定搭配”、“定式”，或者更正式一点可以叫“模版”。大多数情况下，我们是根据模版来说出合理的话来。而不同的人的说话模版可能有所不同，这就是个人的说话风格，甚至是“口头禅”。

点击阅读全文...

在本文，我们介绍“套路宝典”第一式——“当机立断”：1、导出平均字信息熵的概念，然后基于最小熵原理推导出互信息公式；2、并且完成词库的无监督构建、给出一元分词模型的信息熵诠释，从而展示有关生成套路、识别套路的基本方法和技巧。

这既是最小熵原理的第一个使用案例，也是整个“套路宝典”的总纲。

你练或者不练，套路就在那里，不增不减。

为什么需要词语

从上一篇文章可以看到，假设我们根本不懂中文，那么我们一开始会将中文看成是一系列“字”随机组合的字符串，但是慢慢地我们会发现上下文是有联系的，它并不是“字”的随机组合，它应该是“套路”的随机组合。于是为了减轻我们的记忆成本，我们会去挖掘一些语言的“套路”。第一个“套路”，是相邻的字之间的组合定式，这些组合定式，也就是我们理解的“词”。

平均字信息熵

假如有一批语料，我们将它分好词，以词作为中文的单位，那么每个词的信息量是$-\log p_w$，因此我们就可以计算记忆这批语料所要花费的时间为
$$-\sum_{w\in \text{语料}}\log p_w\tag{2.1}$$
这里$w\in \text{语料}$是对语料逐词求和，不用去重。如果不分词，按照字来理解，那么需要的时间为
$$-\sum_{c\in \text{语料}}\log p_c\tag{2.2}$$

点击阅读全文...

话在开头

在深度学习等端到端方案已经逐步席卷NLP的今天，你是否还愿意去思考自然语言背后的基本原理？我们常说“文本挖掘”，你真的感受到了“挖掘”的味道了吗？

无意中的邂逅

前段时间看了一篇关于无监督句法分析的文章，继而从它的参考文献中发现了论文《Redundancy Reduction as a Strategy for Unsupervised Learning》，这篇论文介绍了如何从去掉空格的英文文章中将英文单词复原。对应到中文，这不就是词库构建吗？于是饶有兴致地细读了一番，发现论文思路清晰、理论完整、结果漂亮，让人赏心悦目。

尽管现在看来，这篇论文的价值不是很大，甚至其结果可能已经被很多人学习过了，但是要注意：这是一篇1993年的论文！在PC机还没有流行的年代，就做出了如此前瞻性的研究。虽然如今深度学习流行，NLP任务越做越复杂，这确实是一大进步，但是我们对NLP原理的真正了解，还不一定超过几十年前的前辈们多少。

这篇论文是通过“去冗余”（Redundancy Reduction）来实现无监督地构建词库的，从信息论的角度来看，“去冗余”就是信息熵的最小化。无监督句法分析那篇文章也指出“信息熵最小化是无监督的NLP的唯一可行的方案”。我进而学习了一些相关资料，并且结合自己的理解思考了一番，发现这个评论确实是耐人寻味。我觉得，不仅仅是NLP，信息熵最小化很可能是所有无监督学习的根本。

点击阅读全文...

话说我觉得我自己最近写文章都喜欢长篇大论了，而且扎堆地来～之前连续写了三篇关于Capsule的介绍，这次轮到VAE了，本文是VAE的第三篇探索，说不准还会有第四篇～不管怎么样，数量不重要，重要的是能把问题都想清楚。尤其是对于VAE这种新奇的建模思维来说，更加值得细细地抠。

这次我们要关心的一个问题是：VAE为什么能成？

估计看VAE的读者都会经历这么几个阶段。第一个阶段是刚读了VAE的介绍，然后云里雾里的，感觉像自编码器又不像自编码器的，反复啃了几遍文字并看了源码之后才知道大概是怎么回事；第二个阶段就是在第一个阶段的基础上，再去细读VAE的原理，诸如隐变量模型、KL散度、变分推断等等，细细看下去，发现虽然折腾来折腾去，最终居然都能看明白了。

这时候读者可能就进入第三个阶段了。在这个阶段中，我们会有诸多疑问，尤其是可行性的疑问：“为什么它这样反复折腾，最终出来模型是可行的？我也有很多想法呀，为什么我的想法就不行？”

前文之要

让我们再不厌其烦地回顾一下前面关于VAE的一些原理。

VAE希望通过隐变量分解来描述数据$X$的分布
$$p(x)=\int p(x|z)p(z)dz,\quad p(x,z) = p(x|z)p(z)\tag{1}$$

点击阅读全文...

源起

前几天写了博文《变分自编码器（一）：原来是这么一回事》，从一种比较通俗的观点来理解变分自编码器（VAE），在那篇文章的视角中，VAE跟普通的自编码器差别不大，无非是多加了噪声并对噪声做了约束。然而，当初我想要弄懂VAE的初衷，是想看看究竟贝叶斯学派的概率图模型究竟是如何与深度学习结合来发挥作用的，如果仅仅是得到一个通俗的理解，那显然是不够的。

所以我对VAE继续思考了几天，试图用更一般的、概率化的语言来把VAE说清楚。事实上，这种思考也能回答通俗理解中无法解答的问题，比如重构损失用MSE好还是交叉熵好、重构损失和KL损失应该怎么平衡，等等。

建议在阅读《变分自编码器（一）：原来是这么一回事》后对本文进行阅读，本文在内容上尽量不与前文重复。

准备

在进入对VAE的描述之前，我觉得有必要把一些概念性的内容讲一下。

点击阅读全文...

过去虽然没有细看，但印象里一直觉得变分自编码器（Variational Auto-Encoder，VAE）是个好东西。于是趁着最近看概率图模型的三分钟热度，我决定也争取把VAE搞懂。于是乎照样翻了网上很多资料，无一例外发现都很含糊，主要的感觉是公式写了一大通，还是迷迷糊糊的，最后好不容易觉得看懂了，再去看看实现的代码，又感觉实现代码跟理论完全不是一回事啊。

终于，东拼西凑再加上我这段时间对概率模型的一些积累，并反复对比原论文《Auto-Encoding Variational Bayes》，最后我觉得我应该是想明白了。其实真正的VAE，跟很多教程说的的还真不大一样，很多教程写了一大通，都没有把模型的要点写出来～于是写了这篇东西，希望通过下面的文字，能把VAE初步讲清楚。

分布变换

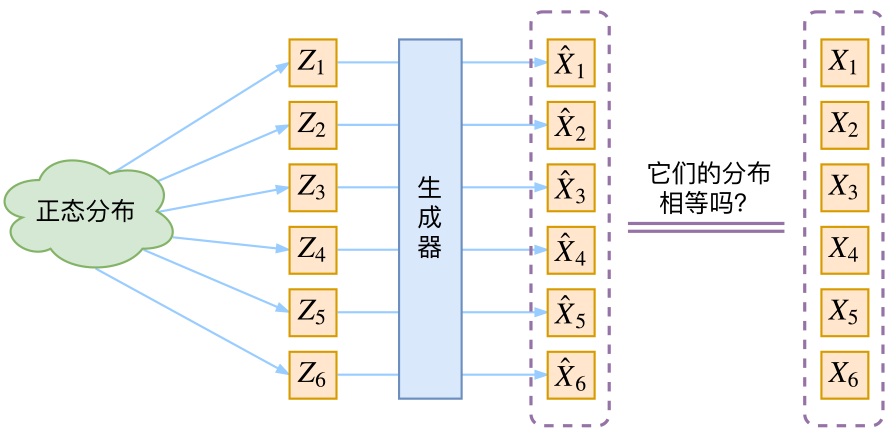
通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量$Z$生成目标数据$X$的模型，但是实现上有所不同。更准确地讲，它们是假设了$Z$服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型$X=g(Z)$，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式

点击阅读全文...

前言

GAN，全称Generative Adversarial Nets，中文名是生成对抗式网络。对于GAN来说，最通俗的解释就是“伪造者-鉴别者”的解释，如艺术画的伪造者和鉴别者。一开始伪造者和鉴别者的水平都不高，但是鉴别者还是比较容易鉴别出伪造者伪造出来的艺术画。但随着伪造者对伪造技术的学习后，其伪造的艺术画会让鉴别者识别错误；或者随着鉴别者对鉴别技术的学习后，能够很简单的鉴别出伪造者伪造的艺术画。这是一个双方不断学习技术，以达到最高的伪造和鉴别水平的过程。 然而，稍微深入了解的读者就会发现，跟现实中的造假者不同，造假者会与时俱进地使用新材料新技术来造假，而GAN最神奇而又让人困惑的地方是它能够将随机噪声映射为我们所希望的正样本，有噪声就有正样本，这不是无本生意吗，多划算～

另一个情况是，自从WGAN提出以来，基本上GAN的主流研究都已经变成了WGAN上去了，但WGAN的形式事实上已经跟“伪造者-鉴别者”差得比较远了。而且WGAN虽然最后的形式并不复杂，但是推导过程却用到了诸多复杂的数学，使得我无心研读原始论文。这迫使我要找从一条简明直观的线索来理解GAN。幸好，经过一段时间的思考，有点收获。

点击阅读全文...