单摆运动级数解:初试同伦分析
By 苏剑林 | 2013-03-13 | 24472位读者 | 引用开始之初,我偶然在图书馆看到了一本名为《超越摄动:同伦分析方法导论》,里边介绍了一种求微分方程近似解的新方法,关键是里边的内容看起来并不是十分难懂,因此我饶有兴致地借来研究了。果然,这是一种非常有趣的方法,在某种意义上来说,还是非常简洁的方法。这解决了我一直以来想要研究的问题:用傅里叶级数来近似描述单摆运动的近似解。当然,它带给我的冲击不仅仅是这些。为了得出周期解,我又同时研究了各种摄动方法的技巧,如消除长期项的PL(Poincaré–Lindstedt)方法。这同时增加了我对各种近似解析方法的了解。从开学到现在快三周的时间,我一直都在研究这些问题。
行星密度与其公转周期(更新)
By 苏剑林 | 2012-10-24 | 29734位读者 | 引用===我与《天文爱好者》不得不说的故事===
去年在订阅2012年的《天文爱好者》时,考虑到之后就要上大学了,所以只是订了半年,因此过了今年六月我就没有看新的《天文爱好者》了。暑假的两个月,还有九月、十月,将近四个月没有看它了,我本以为我已经适应了没有天爱的日子。
大概一个星期前,我在天爱的淘宝网重新买了最近四个月的《天文爱好者》,18日下午,我再见了它。那天晚上,我突然觉得很感动,有种感慨万千的感觉。虽然这么久没有看了,但是再看的感觉是如此的熟悉,如此的温馨。我原来觉得天文只是我的一个业余兴趣,如同生物化学那样,但在那瞬间我明白了我真的爱着天文,而且时间和空间的距离并不能减少我的爱!在那时,我决定了,我一定要从事天文相关专业——虽然我只是一个数学系学生!
==========行星周期下限==========
(2012.10.25:zwhzjh提出攝动力公式有错误,修正了攝动力的计算公式,之前写少了一个因子2,还有在最后的实际检验时,为了追求结果的合理性,忽略了方法的科学性,现在已经进行了修正,欢迎各位提更多意见。)
本文要探讨的东西是我在阅读《天文爱好者》的时候偶然发现的。在发现系外行星以前,人们通常都认为像木星这样的气态巨行星,公转周期都应该在十年以上。因此当瑞士天文学家米歇尔·迈耶和迪戴尔·邱洛兹发现第一颗系外行星时,他们简直无法确信自己的发现,因为这颗类木行星的公转周期只有短短的4.2天!但是经过确认,这的确是一颗系外行星,颠覆了过去的看法。我饶有兴致地研究下去,企图推导出某一密度行星的公转周期下限。
各位读者不妨先估计一下,它会与什么物理量有关?行星质量?母星质量?还是...?
我们经常听说牛顿力学、相对论力学、量子力学等物理名词,也不时会听到“理论力学”。其实,“理论力学”这个名词是不大妥当的,因为这很容易会让人误认为这是一种新的力学体系。而事实上,理论力学并不是像牛顿力学那样是一种力学体系,而是一种研究力学的方法,而研究的对象在多数情况下依然是经典力学(翻开任意一本《理论力学》教程都不难发现这一点)。简单来讲,它把牛顿时代用微积分来研究力学的方法转变为了“变分”,变“常微分”为“偏微分”。看上去这有点“化简为繁”,但事实上这样的一个转变却带来了力学研究的一个巨大的飞跃。
说到这里,也许有的读者会感到害怕了:这里边肯定又涉及了各种高深莫测的高等数学方法,我们只能望而却步。的确,理论力学中的方法很是深奥,纵使是一个优秀的大学数理本科生,也可能要花上一年多时间才能学完一本《理论力学》。可是,通过最小作用量原理的方法去研究物理又显得如此地诱人。难道像我们这些初级人士就无法亲身体验理论力学方法给我们带来的巨大便利和不一样的体验了吗?
唠叨下,关于三体问题周期轨道
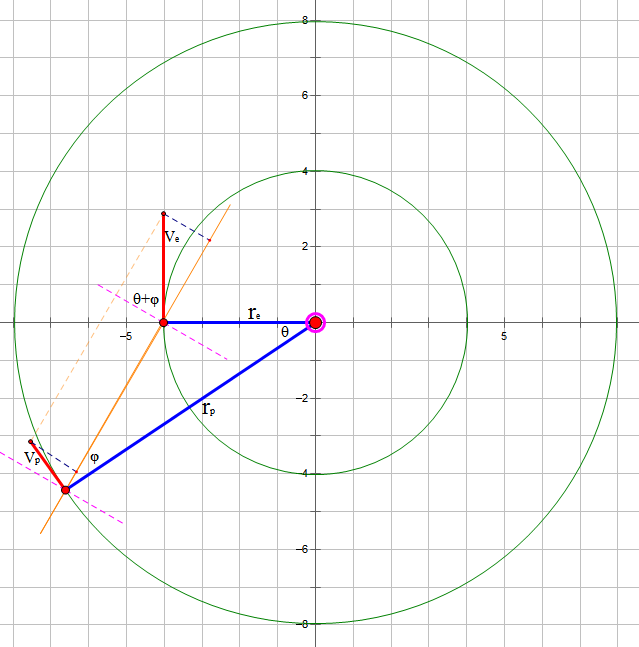
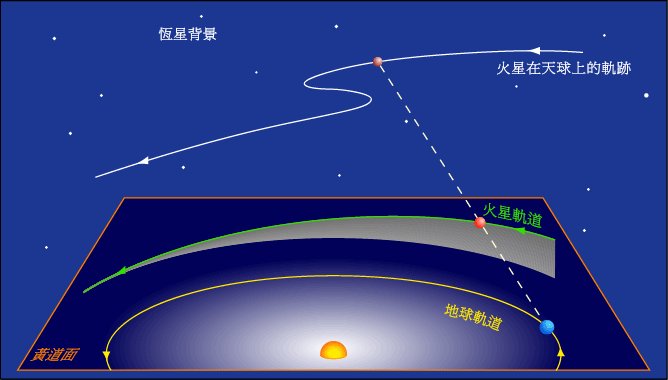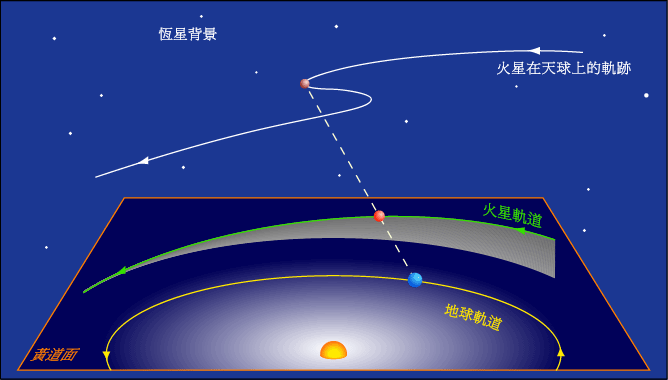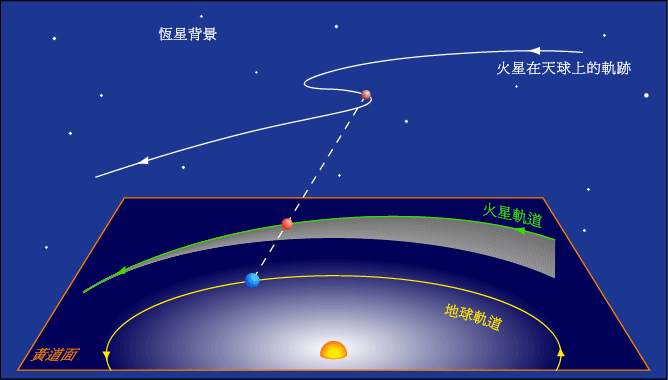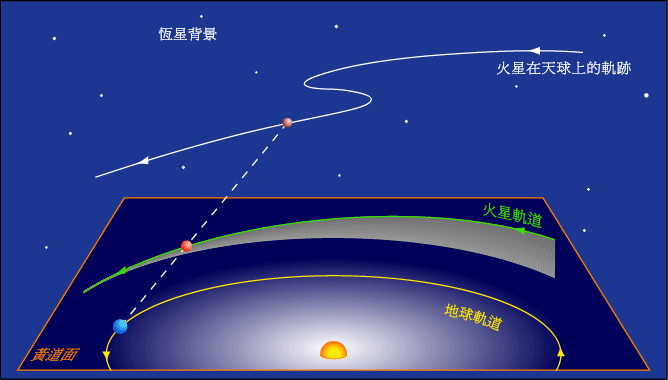
By 苏剑林 | 2011-01-26 | 39089位读者 | 引用关于行星留周期的几何讨论
By 苏剑林 | 2010-10-02 | 20849位读者 | 引用捉弄计划的失败——单摆周期
By 苏剑林 | 2010-06-09 | 55078位读者 | 引用“滴答滴答,滴答滴答——”当我们看到家里的摆钟来回摆动,并且能够准确地报时的时候,有没有想过其中的奥妙呢?
有一天,你想捉弄一下妈妈,把钟摆系上一个重物,心想着钟一定会走得更快,妈妈就会乱套了。可是很快你会失望地发现,摆钟依然准时地走着,没有任何异常,时间仿佛在宣告他的不可控制。你感到非常纳闷:为什么我的计划会失败呢?
据说,世界上第一个研究单摆的人是伽利略,他通过多次实验得出结论:单摆的周期只取决于摆绳的长度,和摆的重量无关。这是你明白了,原来要捉弄妈妈,应该要增加钟摆长度才对...^_^
现在我们来分析一下这个单摆....











最近评论