基于Conditional Layer Normalization的条件文本生成
By 苏剑林 | 2019-12-14 | 117900位读者 | 引用从文章《从语言模型到Seq2Seq:Transformer如戏,全靠Mask》中我们可以知道,只要配合适当的Attention Mask,Bert(或者其他Transformer模型)就可以用来做无条件生成(Language Model)和序列翻译(Seq2Seq)任务。
可如果是有条件生成呢?比如控制文本的类别,按类别随机生成文本,也就是Conditional Language Model;又比如传入一副图像,来生成一段相关的文本描述,也就是Image Caption。
相关工作
八月份的论文《Encoder-Agnostic Adaptation for Conditional Language Generation》比较系统地分析了利用预训练模型做条件生成的几种方案;九月份有一篇论文《CTRL: A Conditional Transformer Language Model for Controllable Generation》提供了一个基于条件生成来预训练的模型,不过这本质还是跟GPT一样的语言模型,只能以文字输入为条件;而最近的论文《Plug and Play Language Models: a Simple Approach to Controlled Text Generation》将$p(x|y)$转化为$p(x)p(y|x)$来探究基于预训练模型的条件生成。
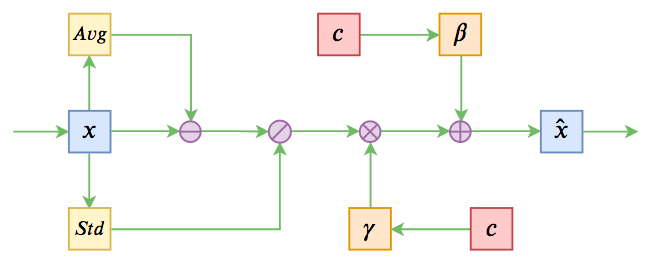
不过这些经典工作都不是本文要介绍的。本文关注的是以一个固定长度的向量作为条件的文本生成的场景,而方法是Conditional Layer Normalization——把条件融合到Layer Normalization的$\beta$和$\gamma$中去。
Keras:Tensorflow的黄金标准
By 苏剑林 | 2019-11-06 | 77396位读者 | 引用这两周投入了比较多的精力去做bert4keras的开发,除了一些API的规范化工作外,其余的主要工作量是构建预训练部分的代码。在昨天,预训练代码基本构建完毕,并同时在TPU/多GPU环境下测试通过,从而有志(有算力)改进预训练模型的同学多了一个选择。——这可能是目前最为清晰易懂的bert及其预训练代码。
预训练代码链接: https://github.com/bojone/bert4keras/tree/master/pretraining
经过这两周的开发(填坑),笔者的最大感想就是:Keras已经成为了tensorflow的黄金标准了。只要你的代码按照Keras的标准规范写,那可以轻松迁移到tf.keras中去,继而可以非常轻松地在TPU或多GPU环境下训练,真正的几乎是一劳永逸。相反,如果你的写法过于灵活,包括像笔者之前介绍的很多“移花接木”式的Keras技巧,就可能会有不少问题,甚至可能出现的一种情况是:就算你已经在多GPU上跑通了,在TPU上你也死活调不通。
从DCGAN到SELF-MOD:GAN的模型架构发展一览
By 苏剑林 | 2019-04-19 | 82074位读者 | 引用事实上,O-GAN的发现,已经达到了我对GAN的理想追求,使得我可以很惬意地跳出GAN的大坑了。所以现在我会试图探索更多更广的研究方向,比如NLP中还没做过的任务,又比如图神经网络,又或者其他有趣的东西。
不过,在此之前,我想把之前的GAN的学习结果都记录下来。
这篇文章中,我们来梳理一下GAN的架构发展情况,当然主要的是生成器的发展,判别器一直以来的变动都不大。还有,本文介绍的是GAN在图像方面的模型架构发展,跟NLP的SeqGAN没什么关系。
此外,关于GAN的基本科普,本文就不再赘述了。
JoSE:球面上的词向量和句向量
By 苏剑林 | 2019-11-11 | 70060位读者 | 引用这篇文章介绍一个发表在NeurIPS 2019的做词向量和句向量的模型JoSE(Joint Spherical Embedding),论文名字是《Spherical Text Embedding》。JoSE模型思想上和方法上传承自Doc2Vec,评测结果更加漂亮,但写作有点故弄玄虚之感。不过笔者决定写这篇文章,是因为觉得里边的某些分析过程有点意思,可能会对一般的优化问题都有些参考价值。
优化目标
在思想上,这篇文章基本上跟Doc2Vec是一致的:为了训练句向量,把句子用一个id表示,然后把它也当作一个词,跟句内所有的词都共现,最后训练一个Skip Gram模型,训练的方式都是基于负采样的。跟Doc2Vec不一样的是,JoSE将全体向量的模长都归一化了(也就是只考虑单位球面上的向量),然后训练目标没有用交叉熵,而是用hinge loss:
\begin{equation}\max(0, m - \cos(\boldsymbol{u}, \boldsymbol{v}) - \cos(\boldsymbol{u}, \boldsymbol{d}) + \cos(\boldsymbol{u}', \boldsymbol{v}) + \cos(\boldsymbol{u}', \boldsymbol{d})\label{eq:loss}\end{equation}
从动力学角度看优化算法(四):GAN的第三个阶段
By 苏剑林 | 2019-05-03 | 98376位读者 | 引用在对GAN的学习和思考过程中,我发现我不仅学习到了一种有效的生成模型,而且它全面地促进了我对各种模型各方面的理解,比如模型的优化和理解视角、正则项的意义、损失函数与概率分布的联系、概率推断等等。GAN不单单是一个“造假的玩具”,而是具有深刻意义的概率模型和推断方法。
作为事后的总结,我觉得对GAN的理解可以粗糙地分为三个阶段:
1、样本阶段:在这个阶段中,我们了解了GAN的“鉴别者-造假者”诠释,懂得从这个原理出发来写出基本的GAN公式(如原始GAN、LSGAN),比如判别器和生成器的loss,并且完成简单GAN的训练;同时,我们知道GAN有能力让图片更“真”,利用这个特性可以把GAN嵌入到一些综合模型中。
2、分布阶段:在这个阶段中,我们会从概率分布及其散度的视角来分析GAN,典型的例子是WGAN和f-GAN,同时能基本理解GAN的训练困难问题,比如梯度消失和mode collapse等,甚至能基本地了解变分推断,懂得自己写出一些概率散度,继而构造一些新的GAN形式。
3、动力学阶段:在这个阶段中,我们开始结合优化器来分析GAN的收敛过程,试图了解GAN是否能真的达到理论的均衡点,进而理解GAN的loss和正则项等因素如何影响的收敛过程,由此可以针对性地提出一些训练策略,引导GAN模型到达理论均衡点,从而提高GAN的效果。
Self-Orthogonality Module:一个即插即用的核正交化模块
By 苏剑林 | 2020-01-12 | 55511位读者 | 引用前些天刷Arxiv看到新文章《Self-Orthogonality Module: A Network Architecture Plug-in for Learning Orthogonal Filters》(下面简称“原论文”),看上去似乎有点意思,于是阅读了一番,读完确实有些收获,在此记录分享一下。
给全连接或者卷积模型的核加上带有正交化倾向的正则项,是不少模型的需求,比如大名鼎鼎的BigGAN就加入了类似的正则项。而这篇论文则引入了一个新的正则项,笔者认为整个分析过程颇为有趣,可以一读。
为什么希望正交?
在开始之前,我们先约定:本文所出现的所有一维向量都代表列向量。那么,现在假设有一个$d$维的输入样本$\boldsymbol{x}\in \mathbb{R}^d$,经过全连接或卷积层时,其核心运算就是:
\begin{equation}\boldsymbol{y}^{\top}=\boldsymbol{x}^{\top}\boldsymbol{W},\quad \boldsymbol{W}\triangleq (\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_k)\label{eq:k}\end{equation}
其中$\boldsymbol{W}\in \mathbb{R}^{d\times k}$是一个矩阵,它就被称“核”(全连接核/卷积核),而$\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_k\in \mathbb{R}^{d}$是该矩阵的各个列向量。
函数光滑化杂谈:不可导函数的可导逼近
By 苏剑林 | 2019-05-20 | 127025位读者 | 引用一般来说,神经网络处理的东西都是连续的浮点数,标准的输出也是连续型的数字。但实际问题中,我们很多时候都需要一个离散的结果,比如分类问题中我们希望输出正确的类别,“类别”是离散的,“类别的概率”才是连续的;又比如我们很多任务的评测指标实际上都是离散的,比如分类问题的正确率和F1、机器翻译中的BLEU,等等。
还是以分类问题为例,常见的评测指标是正确率,而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联,但它们不是绝对的单调相关关系。换句话说,交叉熵下降了,正确率不一定上升。显然,如果能用正确率的相反数做损失函数,那是最理想的,但正确率是不可导的(涉及到$\text{argmax}$等操作),所以没法直接用。
这时候一般有两种解决方案;一是动用强化学习,将正确率设为奖励函数,这是“用牛刀杀鸡”的方案;另外一种是试图给正确率找一个光滑可导的近似公式。本文就来探讨一下常见的不可导函数的光滑近似,有时候我们称之为“光滑化”,有时候我们也称之为“软化”。
max
后面谈到的大部分内容,基础点就是$\max$操作的光滑近似,我们有:
\begin{equation}\max(x_1,x_2,\dots,x_n) = \lim_{K\to +\infty}\frac{1}{K}\log\left(\sum_{i=1}^n e^{K x_i}\right)\end{equation}
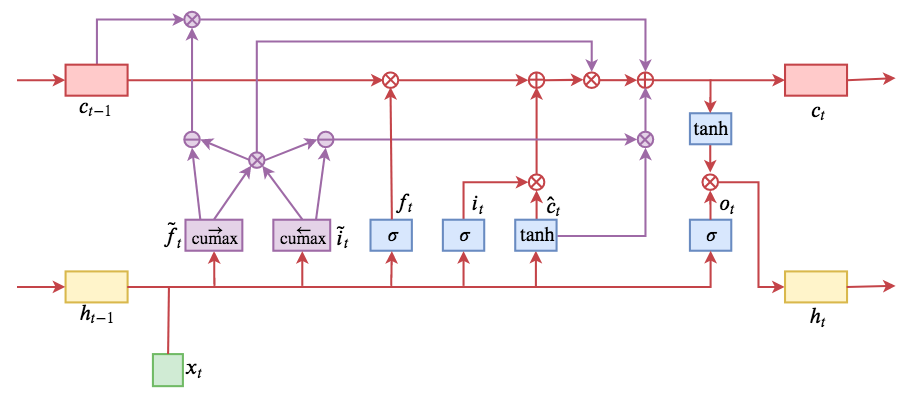
ON-LSTM:用有序神经元表达层次结构
By 苏剑林 | 2019-05-28 | 197175位读者 | 引用今天介绍一个有意思的LSTM变种:ON-LSTM,其中“ON”的全称是“Ordered Neurons”,即有序神经元,换句话说这种LSTM内部的神经元是经过特定排序的,从而能够表达更丰富的信息。ON-LSTM来自文章《Ordered Neurons: Integrating Tree Structures into Recurrent Neural Networks》,顾名思义,将神经元经过特定排序是为了将层级结构(树结构)整合到LSTM中去,从而允许LSTM能自动学习到层级结构信息。这篇论文还有另一个身份:ICLR 2019的两篇最佳论文之一,这表明在神经网络中融合层级结构(而不是纯粹简单地全向链接)是很多学者共同感兴趣的课题。
笔者留意到ON-LSTM是因为机器之心的介绍,里边提到它除了提高了语言模型的效果之外,甚至还可以无监督地学习到句子的句法结构!正是这一点特性深深吸引了我,而它最近获得ICLR 2019最佳论文的认可,更是坚定了我要弄懂它的决心。认真研读、推导了差不多一星期之后,终于有点眉目了,遂写下此文。
在正式介绍ON-LSTM之后,我忍不住要先吐槽一下这篇文章实在是写得太差了,将一个明明很生动形象的设计,讲得异常晦涩难懂,其中的核心是$\tilde{f}_t$和$\tilde{i}_t$的定义,文中几乎没有任何铺垫就贴了出来,也没有多少诠释,开始的读了好几次仍然像天书一样...总之,文章写法实在不敢恭维~










最近评论