科学空间|Scientific Spaces

2009leo-songjian

十一月夜空的主角，将是几个颇具看点的流星雨，南、北金牛以及狮子座流星雨的极大非常值得期待。当然，这段时间观测条件最好的行星还是木星，而到了月底，水星和金星的观测条件也将逐渐转好。其中水星是昏星，日落后在西方的低空中隐约可见，而金星作为晨星将在日出前出现在东方天空中，亮度可达-4.6等。

点击阅读全文...

开发太空天梯

漫话
BoJone认为，科学的意义并非在于无休止地计算，而是利用有限的科学理论来解释尽可能多的自然、生活现象。正因如此，科学家们追求和谐、简洁、优美的科学理论。科学就是想方设法地把未知变成已知，并在此基础上进一步发展。

随着媒体技术的发展，我们接触信息的渠道越来越多。每每我们从互联网或报纸上看到一则科学新闻时，我们几乎都会为之兴奋。但是，外行看热闹，内行看门道。对于真正热爱科学的朋友来说，也许会更加感兴趣新闻内容的来由。也就是说，我们希望进一步了解结论是怎样得出来的——哪怕只是在很浅的层面上认识。

点击阅读全文...

以下内容来源于《天文爱好者》杂志2010年10期（作者庞统，责任编辑李良）。
作为消息通告和交流学习所用，请勿用于商业或其他非法用途
ikaros图片版权：ISAS / JAXA；其余来自互联网搜索得到。

2010年5月21曰，日本用H-2A火箭成功发射了耗资15亿曰元（合1600万美元）的“伊卡洛斯”太阳帆，以检验它是否能够利用太阳能实现加速飞行，从而拉开了研制和发射太阳帆式新型推进航天器高潮的序幕。2010年9月和年底，美国还将先后发射纳帆-D2和光帆-1太阳帆。

ikaros

点击阅读全文...

美“发现”号航天飞机将于11月踏上绝唱之旅

美国航天局29日说，由于“发现”号航天飞机右侧轨道操控系统的加压部分发现两处氦气泄漏，其发射日期将被推迟一天。

“发现”号原计划美国东部时间11月1日发射升空。根据美国航天局最新安排，其发射将推迟到11月2日16时17分(北京时间3日4时17分)。这将是“发现”号计划中的绝唱之旅，也是美国航天飞机今年最后一次飞行任务。

点击阅读全文...

BoJone：阅读本文需要有电离平衡的相关知识作为基础。

这两个星期我们都在学习高中的人教版《化学选修4》中的电离平衡相关知识。虽然我们是“重点班”，可是进展仍然相当地慢。关于电离平衡，有同学向我提出过一个问题：

酸溶液继续加水后，为什么pH会趋于7？（常温常压）

显然，这个问题是很好理解的，因为加水后$H^+$被稀释了。然后我更感兴趣是由此引申出的一个问题：

（强）酸溶液继续加水后，平衡向哪边移动？

点击阅读全文...

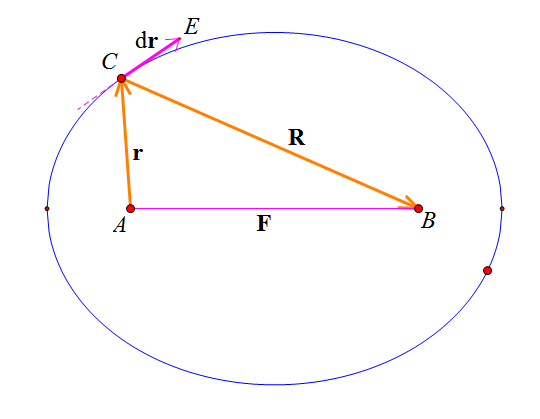
这个星期研究了两道微分方程问题：“导弹跟踪”以及“太阳炉”问题。从中我加深了对微分方程的理解，也熟悉了微分方程的相关运算。仅此记录，权当抛砖引玉。

一、微分方程的本质

很多读者都知道，自从牛顿和莱布尼兹发明微积分之后，微积分就迅速地渗透到了几乎所有的学科，后来发展出许多出色的分支，如变分、微分方程等。众所周知，微分方程是解决很多重要问题的工具。不知道各位读者对微分及微分方程的认识如何？其实对于常微分方程而言，它的本质和我们已经学习过的代数方程一样，只不过相互之间的对应运算关系除了常规的加减乘除幂等之外，还多了两个相互关系：微分和积分。例如对于一阶微分方程$\dot{y}=f(x,y)$，也许大家都认为它是一个二元方程，其实不然，这是一个“四个未知数、三道方程”所组成的方程组，我们可以将它写成

$$dy=f(x,y)dx,y=\int dy,x=\int dx$$

点击阅读全文...

很多读者都知道，反射望远镜、射电望远镜、太阳能集热器等都有一个抛物状的面，它们都是利用了抛物面能将平行射入的光汇聚到一个点（焦点）上的性质。如果问为什么抛物面具有此性质，相信很多高中生都可以利用抛物线的相关知识来证明。但是，如果反过来问：为什么具有此性质的曲面是抛物面？相信会难倒一部分读者。我们来尝试寻找这一曲线（由于对称的原因，这个曲面可以看作由曲线旋转而成，因此我们可以研究曲线）。

世上最大单孔径射电望远镜

点击阅读全文...

在《为什么是抛物线？——聚光面研究》这篇文章里头，我们从光学性质出发，推导出了符合该光学性质的曲线为抛物线，同时我们也不禁感到了向量分析的美妙。也许有的读者会意犹未尽：圆锥曲线有三种，文章只介绍了一种。那好，在这篇文章里，我们就从另外两个光学性质出发，推导出符合这两个光学性质的曲线（椭圆、双曲线）。

（注：在下面的描述中，橙色加粗向量表示光线，曲线表示反射面。）

一、从一个点发出的光线经过曲线（面）反射后汇集到另外一个点上。

椭圆的光学性质

点击阅读全文...