施密特系统的校正镜方程求解
By 苏剑林 | 2011-02-11 | 33254位读者 | 引用非抛物面望远镜的校正镜方程求解
The Corrector Plate of Non-parabola Telescope
本文在牧夫天文论坛的讨论:
http://www.astronomy.ac/bbs/thread-160257-1-1.html
为了克服折射望远镜的色差问题,1670年,牛顿制造了第一台实用的反射式望远镜,将望远镜的主镜由玻璃透镜换成了抛物反射面,从而消除了色差。然而,相比球面镜,大口径的抛物面并不容易磨制。因为制作大球面镜只需要将曲率相等的小镜片相对自由组合在一起就行了,而抛物线每点的曲率并不相等,所以需要逐个磨制曲率不等的小镜片,并按照严格的顺序组合起来。这无疑大大增加了磨制难度。
为了解决这一难题,天文学家们想到了一个折衷的办法:以球面为主镜,并配以校正镜来校正球差。迎着这一思路,施密特望远镜随之而生。而当代的大望远镜基本上都是沿用这一思路。然而,校正镜是一个比抛物面更加复杂的四次曲面,磨制工艺要求更高,因此,校正镜也不宜过大。
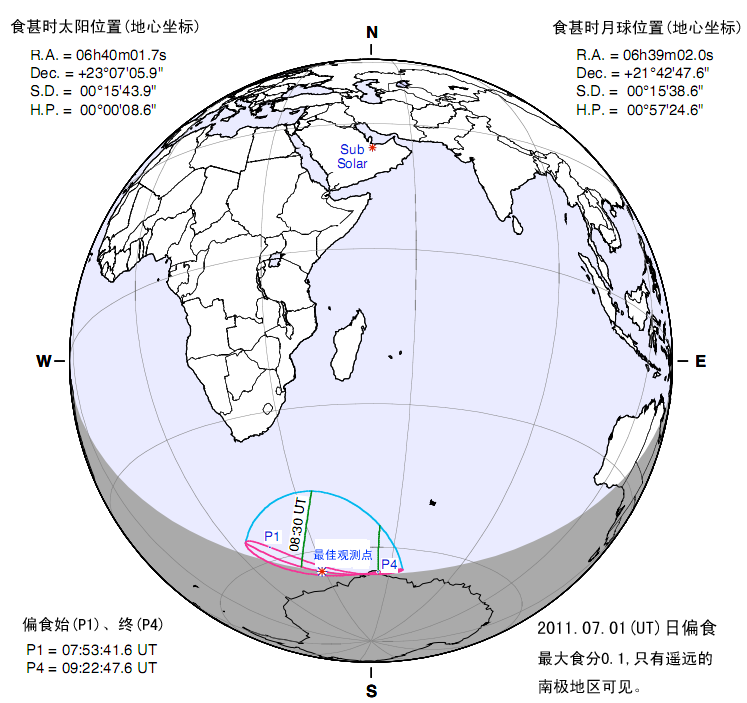
科学空间:2011年7月重要天象
By 苏剑林 | 2011-07-06 | 23556位读者 | 引用费曼路径积分思想的发展(一)
By 苏剑林 | 2012-12-26 | 29115位读者 | 引用注:这是郝刘祥前辈的一篇论文,98年的时候发表在《自然辩证法通讯》上,里边讲述了费曼以及路径积分的相关故事。我从网上下载下来,原文是很粗糙的pdf文件,我特意将它转化为网页文件,供大家欣赏。有些公式很模糊,所以我已经到图书馆查找了原文,但是由于作者非理论物理专业人员,还不确定部分公式是否正确,请读者慎读。原文较长,将分开几篇来发。如果涉及到版权问题,请作者告之(bojone@spaces.ac.cn),我将会尽快处理掉。
自然辩证法通讯(JOURNAL OF DIALECTICS OF NATURE)
第二十卷总115期,1998第3期
郝刘祥
摘要:该文首先阐述了 Richard Feynman为解决经典电动力学的发散问题而做的艰苦努力,进而论述了这种努力的副产品何以使他偏爱作用量表述,以及他是如何在Dirac文章的启发下得到非相对论量子力学的第三种形式--作用量量子化方案的。文章的第三部分叙述了费曼将其方案推广到相对论情形的尝试和费曼图的由来。最后,该文试图就路径积分方法在量子场论等领域中的广泛应用以及费曼对量子场论的重大疑惑作一简要的说明。
关键词:费曼,作用量,几率幅,路径积分
农村的孩子免不了常做家务,当然我家也没有什么特别沉重的家务,通常都是扫地、做饭、洗菜这些简单的活儿。说到洗菜,洗完菜后总喜欢边放水边搅水,然后就在水面上形成一个颇为有趣的漩涡。现在我们从数学物理的角度来分析一下这个漩涡。
在讲洗手盆的漩涡之前,我们先来看一下一个比较类似的、更古老的问题——牛顿的旋转液面问题。牛顿假设有一个水桶(假设为圆柱形吧,但这不重要),水桶在绕自己的中轴线匀角速度旋转,直到桶内的水也随着匀角速度旋转(即水与水桶相对静止),此时水的液面形状是凹的,我们来看看该液面的形状。
牛顿的水桶
要分析形状,我们还要回顾之前提到过的流体静力学平衡:
http://kexue.fm/archives/1964/
【理解黎曼几何】3. 测地线
By 苏剑林 | 2016-10-15 | 57527位读者 | 引用测地线
黎曼度量应该是不难理解的,在微分几何的教材中,我们就已经学习过曲面的“第一基本形式”了,事实上两者是同样的东西,只不过看待问题的角度不同,微分几何是把曲面看成是三维空间中的二维子集,而黎曼几何则是从二维曲面本身内蕴地研究几何问题。
几何关心什么问题呢?事实上,几何关心的是与变换无关的“客观实体”(或者说是在变换之下不变的东西),这也是几何的定义。根据Klein提出的《埃尔朗根纲领》,几何就是研究在某种变换(群)下的不变性质的学科。如果把变换局限为刚性变换(平移、旋转、反射),那么就是欧式几何;如果变换为一般的线性变换,那就是仿射几何。而黎曼几何关心的是与一切坐标都无关的客观实体。比如说,我有一个向量,方向和大小都确定了,在直角坐标系是$(1, 1)$,在极坐标系是$(\sqrt{2}, \pi/4)$,虽然两个坐标系下的分量不同,但它们都是指代同一个向量。也就是说向量本身是客观存在的实体,跟所使用的坐标无关。从代数层面看,就是只要能够通过某种坐标变换相互得到的,我们就认为它们是同一个东西。
因此,在学习黎曼几何时,往“客观实体”方向思考,总是有益的。
有了度规,可以很自然地引入“测地线”这一实体。狭义来看,它就是两点间的最短线——是平直空间的直线段概念的推广(实际的测地线不一定是最短的,但我们先不纠结细节,而且这不妨碍我们理解它,因为测地线至少是局部最短的)。不难想到,只要两点确定了,那么不管使用什么坐标,两点间的最短线就已经确定了,因此这显然是一个客观实体。有一个简单的类比,就是不管怎么坐标变换,一个函数$f(x)$的图像极值点总是确定的——不管你变还是不变,它就在那儿,不偏不倚。
从一个单位向量变换到另一个单位向量的正交矩阵
By 苏剑林 | 2021-06-05 | 45259位读者 | 引用这篇文章我们来讨论一个比较实用的线性代数问题:
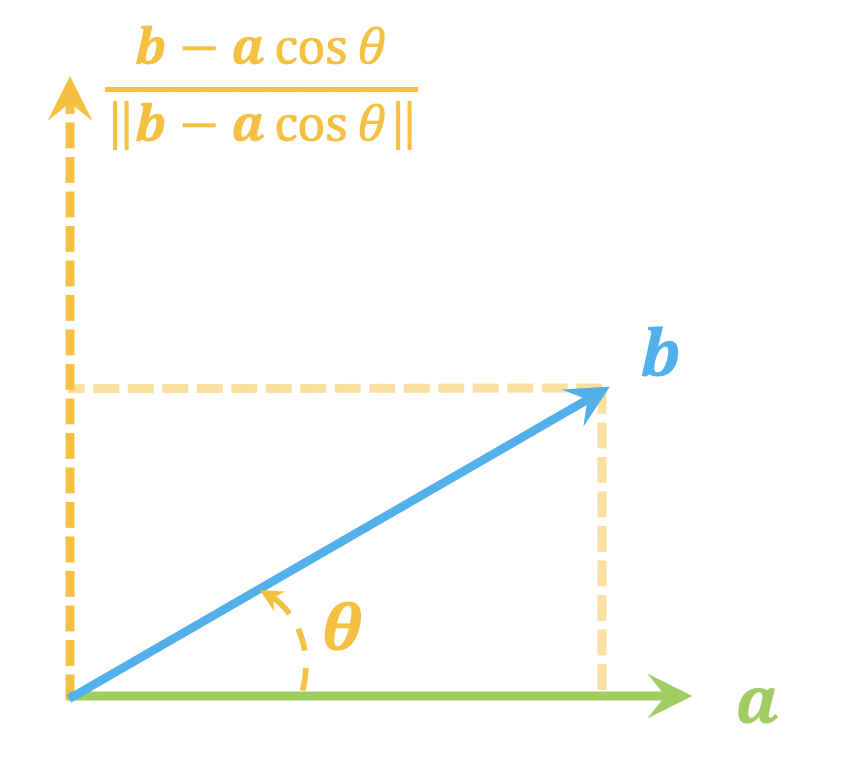
给定两个$d$维单位(列)向量$\boldsymbol{a},\boldsymbol{b}$,求一个正交矩阵$\boldsymbol{T}$,使得$\boldsymbol{b}=\boldsymbol{T}\boldsymbol{a}$。
由于两个向量模长相同,所以很显然这样的正交矩阵必然存在,那么,我们怎么把它找出来呢?
二维
不难想象,这本质上就是$\boldsymbol{a},\boldsymbol{b}$构成的二维子平面下的向量变换(比如旋转或者镜面反射)问题,所以我们先考虑$d=2$的情形。
低秩近似之路(二):SVD
By 苏剑林 | 2024-10-01 | 18248位读者 | 引用上一篇文章中我们介绍了“伪逆”,它关系到给定矩阵$\boldsymbol{M}$和$\boldsymbol{A}$(或$\boldsymbol{B}$)时优化目标$\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$的最优解。这篇文章我们来关注$\boldsymbol{A},\boldsymbol{B}$都不给出时的最优解,即
\begin{equation}\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2\label{eq:loss-ab}\end{equation}
其中$\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{M}\in\mathbb{R}^{n\times m},r < \min(n,m)$。说白了,这就是要寻找矩阵$\boldsymbol{M}$的“最优$r$秩近似(秩不超过$r$的最优近似)”。而要解决这个问题,就需要请出大名鼎鼎的“SVD(奇异值分解)”了。虽然本系列把伪逆作为开篇,但它的“名声”远不如SVD,听过甚至用过SVD但没听说过伪逆的应该大有人在,包括笔者也是先了解SVD后才看到伪逆。
接下来,我们将围绕着矩阵的最优低秩近似来展开介绍SVD。
结论初探
对于任意矩阵$\boldsymbol{M}\in\mathbb{R}^{n\times m}$,都可以找到如下形式的奇异值分解(SVD,Singular Value Decomposition):
\begin{equation}\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\end{equation}










最近评论