“未解之谜”：为何不讲中点矩形法则？

前言

在之前的一些文章中，我们已经指出过现行教材的一些毛病。比如主次不当（最明显的是那些一上来就讲线性方程组的线性代数教程）、缺乏直观性、缺少引导性等，我想其中最主要的原因可能是过于随大流了，别人怎么编我们也跟着怎么编，缺乏自己的观点和逻辑，因此导致一些常见的毛病就一直流传了下来。也许正因如此，就导致了有那么一种奇怪的现象——明明有一种计算量少的、精确度高一些的方法，教科书几乎从未提及；另外一种计算量稍大、精确度稍低的方法，但每一本同类教科书都讲述了它。不能不说这是一个“未解之谜”......

本文要讲的就是这样的两种方法，它们分别是用来求定积分近似值的“中点矩形法则”和“梯形法则”。对于后者我想绝大多数学习过微积分的朋友都会有印象，它就是那个几乎出现在了所有微积分教材的方法；而前者我相信不少读者都未曾听闻，但让人意外的是，它的计算量稍低，精确度却稍高。本文就简单介绍这两种方法，并且比较它们的精度。而本文的独特之处在于，证明过程沿用了《复分析:可视化方法》的思路，使用几何方法漂亮地估计误差！

我们的目标是在难以精确计算的情况下，通过一定的方法求出$\int_a^b f(x)dx$的近似值，这些方法基本上都是利用了积分即面积的思想。

两种不同的方法

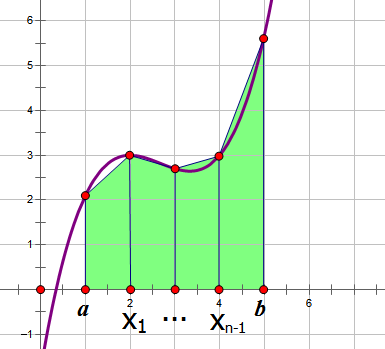
梯形法则的思想挺简单的，如图，我们把[a,b]区间等分为n份，每份长度为h，当然这里的等分不是必须的，但是等分有利于简化计算。然后将每个点$f(a),f(x_1),...,f(x_{n-1}),f(b)$顺次连起来，得到n个梯形。把这n个梯形的面积加起来，就得到了$\int_a^b f(x)dx$的近似值了。于是我们可以得到下面的结果：

$$\begin{aligned}\int_a^b f(x)dx \approx \frac{f(a)+f(x_1)}{2}\cdot h+\frac{f(x_1)+f(x_2)}{2}\cdot h+...+\frac{f(x_{n-1})+f(b)}{2}\cdot h \\ =[\frac{f(a)+f(b)}{2}+\sum_{i=1}^{n-1}f(x_i)]\cdot h\end{aligned}\tag{1}$$
直觉告诉我们，等分的份数n越大，即h越小，误差也会越小。具体的精度分析我们后面再谈及。现在我们继续来看另一种求定积分的近似值的方法——中点矩形法则。

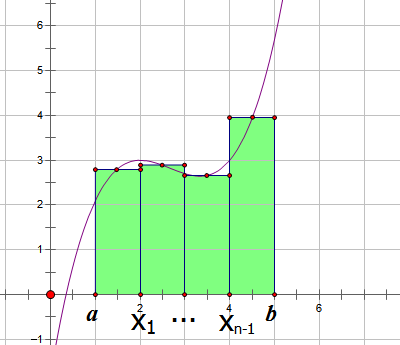
它的思路似乎更加显然。我们同样将[a,b]区间等分为n份，每份长度为h。然后我们取每一份的中点来计算f(x)，然后在每一个小区间都作长为f(x)宽为h的矩形，最后把每一个矩形的面积加起来。于是我们得到了以下公式：

$$\begin{aligned}\int_a^b f(x)dx \approx f(\frac{a+x_1}{2})\cdot h+f(\frac{x_1+x_2}{2})\cdot h+...+f(\frac{x_{n-1}+b}{2})\cdot h \\ =[f(\frac{a+x_1}{2})+f(\frac{x_1+x_2}{2})+...+f(\frac{x_{n-1}+b}{2})]h\end{aligned}\tag{2}$$
按照计算量来看，公式(1)需要计算(n+1)个节点（即f(x)）的值，公式(2)只需要计算n个节点的值，显然单从这一点看公式(2)就略胜一筹了。那么它们各自的精确度又怎样呢？一种很棒的几何思路出场了......

误差分析

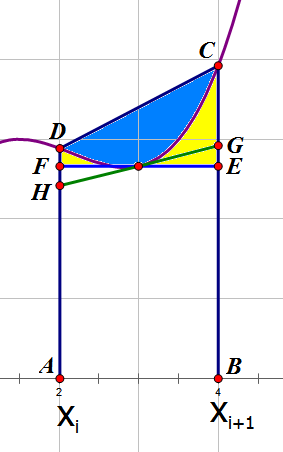
我们要“化整为零”，先把其中的一个小区间独立出来研究误差。我们选取足够小的h让区间内的那一小部分曲线具有单一的凸性（要不就是凸上，要不就是凹下）。图片绘有梯形法则和中点矩形法则的思路。

梯形法则给出的误差是直线DC与曲线围成的面积（蓝色部分），中点矩形法则给出的误差是直线EF与曲线围成的面积（黄色部分），一眼看上去我们就可以感觉蓝色部分面积会比黄色部分要大，这很直观地告诉我们梯形法则误差更大。当然万事不能单凭感觉，我们需要进一步证明。从图上很容易看出梯形法则的估算比准确值要大（仅仅是在本图的这种情况才是），但中点矩形却没有那么直观（中点的水平直线EF不一定是切线，它和原曲线可能有交点），一个绝妙的技巧是以中点为旋转中心，将EF旋转至与原曲线相切的GH直线为止，旋转后矩形ABEF变成了梯形ABGH，但是很显然面积不变的，所以我们也容易看出梯形ABGH面积比原曲线下方的面积要小，即中点矩形法则的估算比准确值要大。

事实上，从一般情况来讲，定积分的准确值就夹在梯形法则和中点矩形法则两者给出的结果之间。

这就告诉我们，两个方法的最大误差都不会超过四边形CDHG的面积，我们要做的就是求出它和h的关系。当h很小时，我们不妨把原曲线看成一段圆弧，然后将图形旋转一下，使得直线GH水平放置，设$|GH|=a$，而h和|GH|是成正比的，两者在某种程度下可以互换。

此时四边形CDHG已被我们近似看成了矩形了，它的面积是$\Delta S=|GH|*|PQ|$，而$|DP|^2=|OP|*|PQ|$。

所以$\Delta S=\frac{|GH|^3}{4|OP|}\propto |GH|^3 \propto h^3$

这里只算了每一份的误差，由于总误差还得把每一份误差累积起来，所以总误差为$\Delta \propto h^2$

其实理论分析告诉我们，两者的误差的确都在$h^2$这个数量级上。但是两者的相对误差如何？我们得计算一下蓝色面积（S₁）和黄色面积（S₂）之比。

$$\begin{aligned}S_1=r^2 \theta-r \cos\theta\cdot r \sin\theta=r^2 \theta-\frac{1}{2} r^2 \sin2\theta \\ S_2=2r \sin\theta\cdot r(1-\cos\theta)-(r^2 \theta-\frac{1}{2} r^2 \sin2\theta)=2r^2 \sin\theta-r^2 \theta-\frac{1}{2} r^2 \sin2\theta\end{aligned}$$

用泰勒级数展开到三阶，得到
$$\begin{aligned}S_1 \approx \frac{4\theta^3}{3} \\ S_2 \approx \frac{2\theta^3}{3}\end{aligned}$$

换句话说，梯形法则的误差是中点矩形法则的两倍！

后语

其实本文的主要目的是把中点矩形法则讲述给各位读者，并且将《复分析:可视化方法》中漂亮的几何证明方法与大家分享，而不在于批判教材。在我看来，中点矩形法则不失为一种很好的方法，疑惑的是教材上居然没有提到它，多亏了这本复分析教材我才知道这一点。不过这其实也提醒了我们在阅读的时候，要多想想为什么，还要多想想“还能怎样”。不能完全迷信书本的权威，因为只有知识才是硬道理。正如读完这篇文章之后，也要用批判性的眼光来重读这篇文章。^_^

另外，值得赞一下的是这本《复分析:可视化方法》，它以一种与常见的复分析教材截然不同的方式来讲述复分析，它强调几何应用，强调直观，也很着重于与物理的联系，这才是复分析教材应该做到的。细细阅读，让我获益匪浅。虽然我还只读了那么几页，但我已经决心要以它作为我自己的标准复分析教材！

转载到请包括本文地址：https://kexue.fm/archives/1668

更详细的转载事宜请参考：《科学空间FAQ》