科学空间|Scientific Spaces

前几天在台湾购买（淘宝代购）的《费曼统计力学》和《费曼计算学》在今天到手了，至此，我的费曼著作收藏基本完成了。

我是一个费曼迷，为费曼的小飞侠人格所吸引，为费曼的物理才能所折服。因此，我甚至像普通人追星那样追崇费曼，收藏他的书籍，还有学习他所发明的物理。

点击阅读全文...

前言：也许你从未见过宇宙飞船，也许你躺在星空下却无所事事，也许你有望远镜却无观测对象，不过，这种心情可以结束了，因为我们可以观测国际空间站！对于这一新闻，无疑是令我们振奋人心的消息！对于天文爱好者来说，更是令人兴奋！不论如何，在繁星中寻找国际空间站是一件无比写意的事情。不仅是能力的挑战，还有耐心！

点击阅读全文...

站长：因为10月8日就上学了，所以不能够及时上网查阅和更新文学奖和和平奖的消息。不过一直在用手机关注着，前天晚上7:00，就一直用手机关注着诺贝尔奖官方网站，最终发现德国人取得了文学奖。而昨天晚上，一个更加惊人的消息发出来了——2009年诺贝尔和平奖的得主竟然是Barack Obama！

太意外了！居然是我们熟悉的美国总统！世界各国也是这样的意外，然而，令人深思的应该是：颁布诺贝尔奖给奥巴马的主要原因，并非肯定奥巴马已经有的成就，应该是鼓励他带领美国为世界作出更大的贡献！由此观之，世界对这位美国总统的期望是十分大的！

中国网10月9日电 据路透社报道，10月9日美国总统贝拉克·奥巴马(Barack Obama )因为世界和平所做的工作，以及呼吁削减世界核武库而赢得2009年诺贝尔和平奖。

点击阅读全文...

阿达马不等式
设有$n$阶实矩阵$\boldsymbol{A}=(a_{ij})_{n\times n}$，那么它的行列式满足阿达马(Hadamard)不等式
$$\begin{equation}
\left(\det \boldsymbol{A}\right)^2 \leq \prod\limits_{i=1}^{n}\left(a_{1i}^2+a_{2i}^2+\dots+a_{ni}^2\right)
\end{equation}$$

这是阿达马在1893年首先发表的。根据体积就是行列式的说法，上述不等式具有相当明显的几何意义。当$n=2$时，它就是说平行四边形的面积不大于两边长的乘积；当$n=3$时，它就是说平行六面体的体积不大于三条棱长的乘积；高维可以类比。这些结论在几何中几乎都是“显然成立”的东西。因此很难理解为什么这个不等式在1893年才被发现。当然，代数不会接受如此笼统的说法，它需要严格的证明。

点击阅读全文...

伽马函数
$$\Gamma(x)=\int_0^{+\infty}t^{x-1}e^{-t}dt$$
作为阶乘的推广，会让很多初学者感到困惑，对于笔者来说也不例外。一个最自然的问题就是：这般复杂的推广公式是如何得到的？

在cos.name的文章《神奇的伽马函数》中，有比较详细地对伽马函数的历史介绍，笔者细读之后也获益匪浅。但美中不足的是，笔者还是没能从中找到引出伽马函数的一种“自然”的办法。所谓“自然”，并不是说最简单的，而是根据一些基本的性质和定义，直接把伽马函数的表达式反解出来。它的过程和运算也许并不简单，但是思想应当是直接而简洁的。当然，我们不能苛求历史上伽马函数以这种方式诞生，但是作为事后探索是有益的，有助于我们了解伽马函数的特性。于是笔者尝试了以下途径，得到了一些结果，可是也得到了一些困惑。

点击阅读全文...

我小时候一直有个疑问：

直升机上的螺旋桨能不能用来挡雨？

一般的螺旋桨是若干个“条状”物通过旋转对称而形成的，也就是说，它并非一个面，按常理来说，它是没办法用来挡雨的。但是，如果在高速旋转的情况下，甚至假设旋转速度可以任意大，那么我们任意时刻都没有办法穿过它了，这种情况下，它似乎与一个实在的面无异？

力的无穷分解

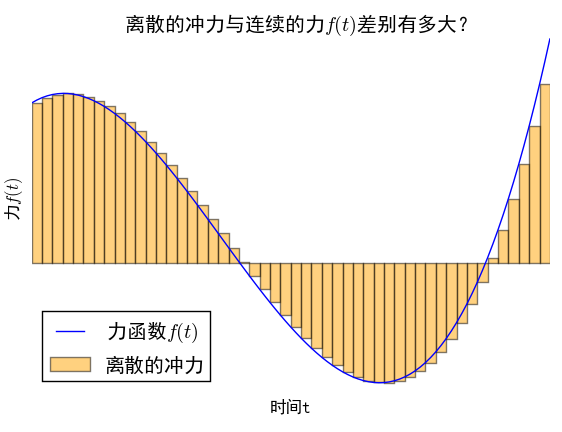
当然，以上只是笔者小时候的一个“异想天开”的念头，读者不必较真。不过，这个疑问跟本文有什么联系呢？我们在研究振动问题之时，通常会遇到在变力的作用下的受迫振动问题，已知变力是时间的函数，比如$f(t)$，然而，虽然知道$f(t)$的具体形式，但是由于$f$的非线性性，加上外力之后的运动，不一定容易求解。然而，如果可以将一个变化的力分段为无数个无穷小时间内的恒力（冲力），那么我们就可以分段讨论我们要研究的运动，而通常来说，恒力的问题会比变力容易。将一个变力离散化，然后再取极限，那么是不是跟原来在变力下的运动是一样的呢？这跟文章开头的疑问有着类似的思想——离线的极限，跟连续本身，是不是等价的？

而让人惊喜的是，在通常的物理系统中，将力分段为无数个小区间内的恒力的做法，能够导致正确的答案，而且，这恰好是线性常微分方程的格林函数法。下面我们来分析这一做法。

点击阅读全文...

如果真有外星人存在，你想对他说什么？

赶紧准备好要说的话，登录澳大利亚一个网站写下来。据英国《每日电讯报》日前报道，该网站将把信息传递到外太空，让外星人“听”见你的问候。

点击阅读全文...

本篇文章是《自然极值》系列最后一篇文章，估计也是2010年最后一篇文章了。在这个美好的2010年，想必大家一定收获匪浅，BoJone也在2010年成长了很多。在2010年的尾声，BoJone和科学空间都祝大家在新的一年里更加开心快乐，在科学的道路上更快速地前行。

在本文，BoJone将与大家讨论求极值的最基本原理。这一探讨思路受到了天才的费恩曼所著《费恩曼物理讲义》的启迪。我们分别对函数求极值（求导）和泛函数极值（变分）进行一些简略的分析。

一、函数求极值

对于一个函数$y=f(x)$，设想它在$x=x_0$处取到最大值，那么显然对于很小的增量$\Delta x$，有
$$f(x_0+\Delta x) \leq f(x_0)\tag{3}$$根据泰勒级数，我们有
$f(x_0+\Delta x)=f(x_0)+f'(x_0)\Delta x$————(4)

点击阅读全文...