地球“黑暗”的一小时
By 苏剑林 | 2010-03-21 | 28604位读者 | 引用【生物总结】到细胞内旅游
By 苏剑林 | 2010-04-05 | 26686位读者 | 引用科学空间:2010年5月重要天象
By 苏剑林 | 2010-04-24 | 21815位读者 | 引用科学空间:2010年3月重要天象
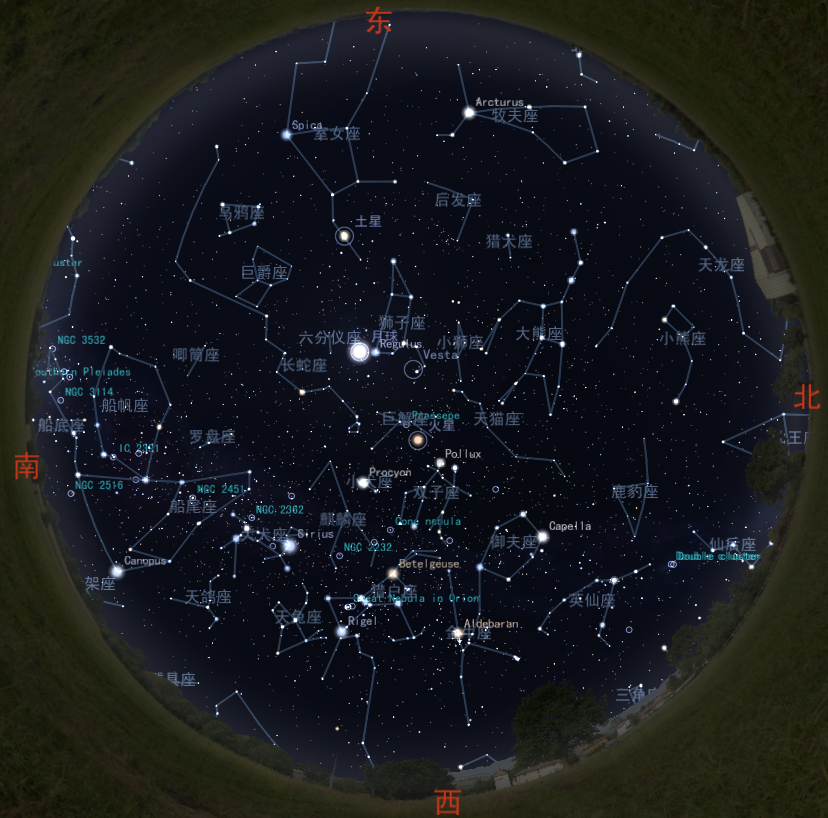
By 苏剑林 | 2010-02-28 | 24055位读者 | 引用 3月份,大地回暖,春暖花开了,精彩的天象在等着我们。这个月天空的主角无疑是美丽的土星,火星和金星也是较好的观测对象。而且3月又正值梅西叶马拉松的好时节,许多有趣、朦胧的深空天体,无疑会极大地挑起我们对神秘的春夜星空的兴趣。这里有一本《梅西叶马拉松全年指导手册》电子书,新手不妨作为入门的参考书。
3月份,大地回暖,春暖花开了,精彩的天象在等着我们。这个月天空的主角无疑是美丽的土星,火星和金星也是较好的观测对象。而且3月又正值梅西叶马拉松的好时节,许多有趣、朦胧的深空天体,无疑会极大地挑起我们对神秘的春夜星空的兴趣。这里有一本《梅西叶马拉松全年指导手册》电子书,新手不妨作为入门的参考书。
梅西叶马拉松是一个自我挑战性相对较强的活动,因为虽然一夜之间所有的梅西耶天体全都亮相,但是因为升起的时间相差很多,有些天体的角度就很低了,并不十分适宜观测,况且一夜之间观测103个天体,即使对星空和器材性能非常熟悉,也需要相当时间(当然啦,你如果有电动赤道仪和导星输入的话,就很简单拉),这会是一个非常辛苦的活动,需要充分准备。 爱好挑战困难者,上吧,探索我们的宇宙!
科学空间:2010年6月重要天象
By 苏剑林 | 2010-05-30 | 29399位读者 | 引用进入六月,除除了水星外肉眼可见的几颗大行星观测条件还不错。前半夜的主要观测目标是金星、火星和土星,他们之间的角距离也在逐渐缩小。后半夜木星升起,我们又有机会一睹这颗太阳系内最大行星的风采了。6月21日是夏至节气,当天北半球白昼是一年中最长的,而夜晚最短,且越往北越短。在北极圈以内地区当天太阳将不会落到地平线以下18度之内时,辉光都会影响到我们目视的极限星等,因此夏至前后一段时间北纬50度以上地区不太适合进行天文观测了。而对于北纬30至40度左右的观测者来说,这期间适合开展人造天体,特别是国际空间站的观测活动。
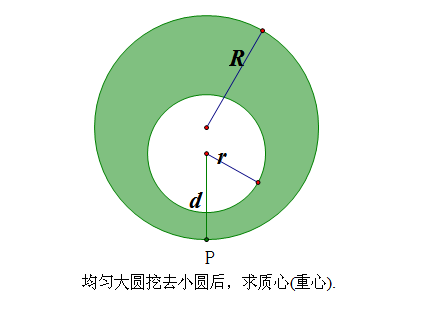
问世间质心(重心)知多少
By 苏剑林 | 2010-07-26 | 47951位读者 | 引用威力巨大的“有向线段”
By 苏剑林 | 2010-06-27 | 21452位读者 | 引用级数求和——近似的无穷级数
By 苏剑林 | 2010-09-10 | 50729位读者 | 引用级数是数学的一门很具有实用性的分支,而级数求和则是级数研究中的核心内容之一。很多问题都可以表示成一个级数的和或积,也就是$\sum_{i=1}^n f(i)$或者是$\prod_{i=1}^n f(i)$类型的运算。其中,$\ln(\prod_{i=1}^n f(i))=\sum_{i=1}^n \ln(f(i))=k$,因此$\prod_{i=1}^n f(i)=e^k$,也就是说,级数求积也可以变为级数求和来计算,换言之我们可以把精力放到级数求和上去。
为了解决一般的级数求和问题,我们考虑以下方程的解:
$$f(x+\epsilon)-f(x)=g(x)\tag{1}$$其中g(x)是已知的以x为变量的函数式,$\epsilon $是常数,初始条件是$f(k)=b$,要求f(x)的表达式。











最近评论