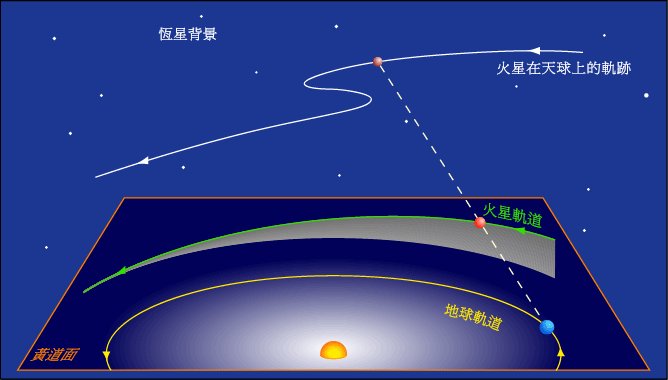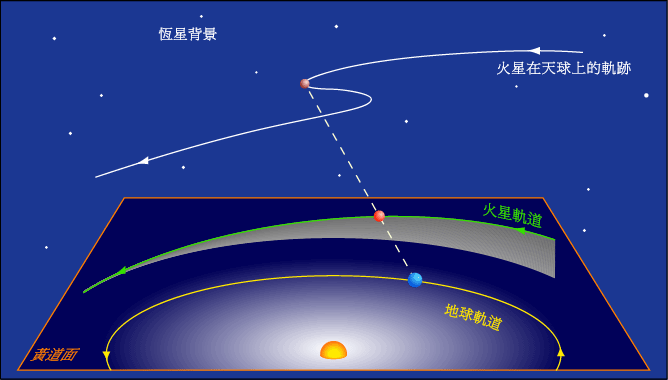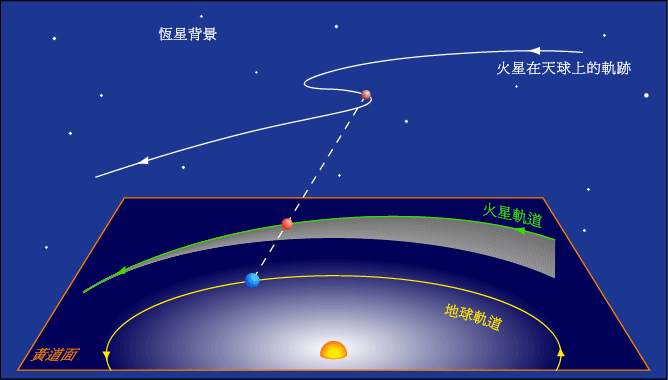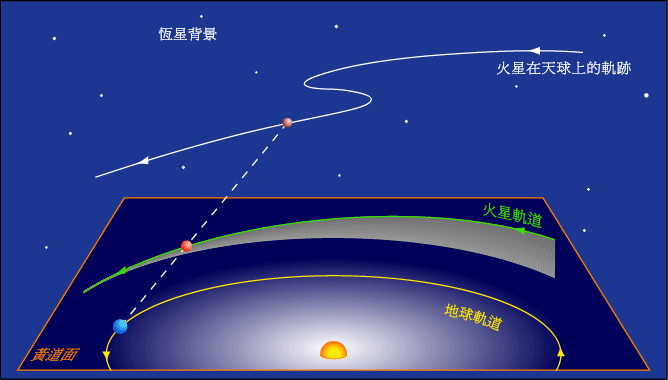
行星的逆行,顺行和留(计算公式)
By 苏剑林 | 2010-04-18 | 70024位读者 | 引用关于自由落体公式的简单修正
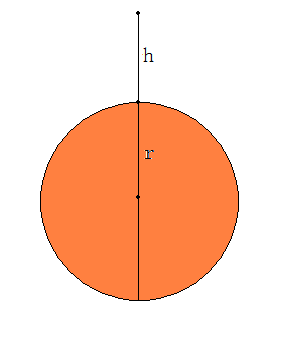
By 苏剑林 | 2010-04-04 | 74229位读者 | 引用自由落体的一般定义是:只考虑吸引天体和被吸引天体的引力因素,忽略其他的运动和大气摩擦等因素,物体从静止(相对于吸引天体)开始接近吸引天体的运动。根据这个定义,假设地球为一个均匀球体,半径为r,质量为M,物体从距离地表h高度处自由落下。求落到地面的时间t,或者根据时间t求h。
令s为t时刻物体左右下落的物体与地表的距离,忽略物体的小质量,那么可以列出微分方程:
$$\frac{d^2 s}{dt^2}=-\frac{GM}{(r+s)^2}\tag{1}$$并且初始条件是$t=0,s=h,\dot{s}=v=0$
在实际应用中,我们不必求出这道微分方程的精确解,因为这个解极其麻烦,在之前曾经讨论过。我们只需要求出一个有足够精确度的近似解就行。
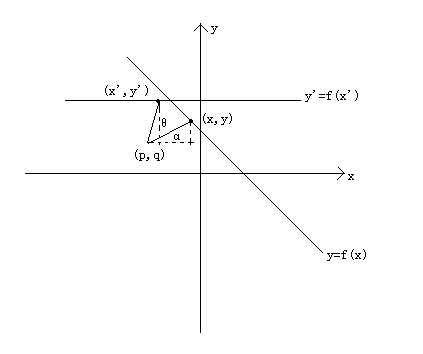
函数图像旋转公式(“想当然”的教训)
By 苏剑林 | 2010-02-09 | 115138位读者 | 引用寒假结束,今天上学了
By 苏剑林 | 2010-02-21 | 30898位读者 | 引用越来越佩服前人,说出了“光阴似箭,日月如梭”的真理。是呀,期末考试仿佛只是在昨天,今天已经又要上学了;俯仰之间,一个月的时间就过去了。
毫无疑问,又因为我的懒惰和不坚持,浪费了我很多的时间。回想一下寒假,我究竟收获了什么呢?主要是两个方面吧:学术和情感。
学术上,主要是数学和天文学里面的内容。数学我主要是深入了微积分方面的内容,把微积分的思想深刻了一点点,把微分方程(组)熟悉了一点点。我有一种很熟悉的感觉:现在自学高等数学,就好比我之前在小学时间学习中学数学。那时候超傻,书本上说了$\lim_{\Delta x->0} f'(x)=\frac{f(x+\Delta x)-f(x)}{\Delta x}$,我看不懂这个式子,整天郁闷$f(x)$是不是指$f\cdot (x)$。不过尽管那时候不懂这些,还是懂应用,我用导数最基本的定义去求极值,得出了一些有趣的发现,使我的兴趣倍增。现在学习微积分也是这样的感觉,我觉得我仅仅是很显浅地接触到,还有很多等待仔细琢磨....
丘成桐摘得沃尔夫奖——获数学界终身成就肯定
By 苏剑林 | 2010-02-27 | 31015位读者 | 引用1月31日晚,华裔数学家丘成桐收到以色列教育部部长兼沃尔夫基金会理事长Gideon Sa’ar亲笔签名的信,通知他获得了2010年的沃尔夫数学奖,原因是他“在几何分析方面的贡献已对几何和物理的许多领域产生深远而引人瞩目的影响”。
1978年开始颁发的沃尔夫奖每年评选一次,分别奖励在农业、化学、数学、医药、物理以及艺术领域中取得突出成绩的人士。其中沃尔夫数学奖影响很大。
今年的颁奖典礼定于5月13日在耶路撒冷举行,丘成桐将与美国数学家丹尼斯·沙利文分享10万美元的数学奖奖金。这是丘成桐继菲尔茨奖后,再次获得国际最顶尖的数学大奖。菲尔茨奖和沃尔夫奖双奖得主,迄今只有13位。
解答不等式的误区...
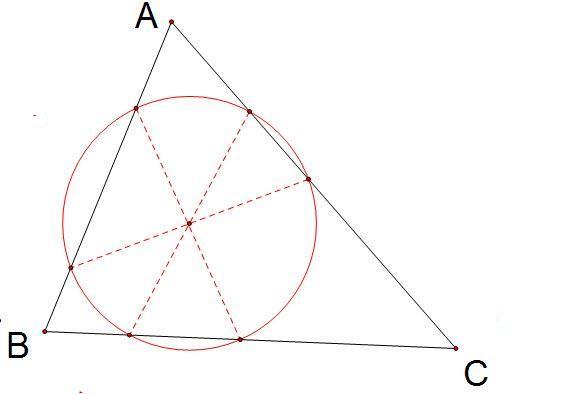
By 苏剑林 | 2010-05-02 | 37493位读者 | 引用神秘的圆——三角形的“六接圆”(添加新方法)
By 苏剑林 | 2010-07-24 | 35509位读者 | 引用《向量》系列——1.向心力公式证明
By 苏剑林 | 2010-07-15 | 63465位读者 | 引用向量在几何和物理中都有极其重要的作用,现在就让我们来看如何用向量研究物理中的圆周运动。
首先我们必须了解一些基础:
1.在向量中,只要一条“向径”($\vec{r}$)就可以描述出物体的运动,而不需要建立坐标系。这就是向量应用于物理的原因:物理定律不应该依赖于坐标系,而向量恰恰也不依赖于坐标系!
2.牛顿第二定律:$\vec{F}=m\vec{a}$
3.以及一些向量的微积分运算等(可以查阅维基百科或者相关资料)
在下面及以后的文章描述中,为了大家的阅读方便,把向量写成$\vec{r}$的形式,而非把字母加粗。一般情况下,在本站的描述中,有$|\vec{r}|=r,|\dot{\vec{r}}|=v,|\ddot{\vec{r}}|=a$。但是,$\dot{r}=\frac{d|\vec{r}|}{dt} != |\dot{\vec{r}}|$










最近评论