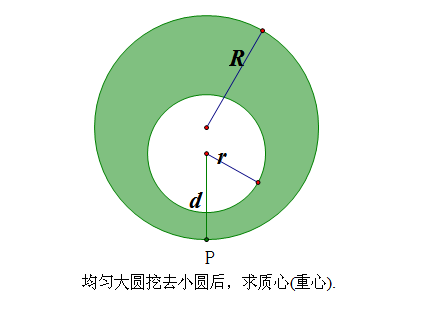
问世间质心(重心)知多少
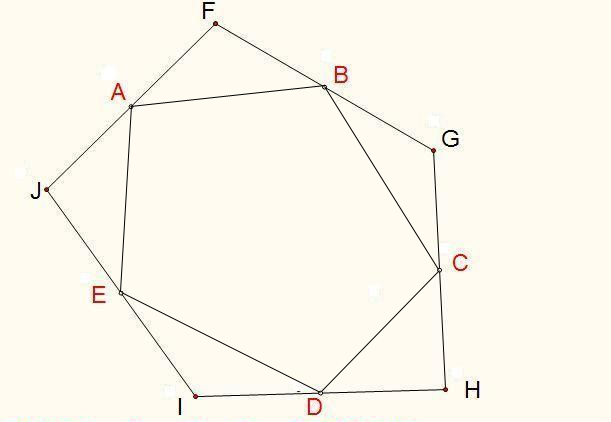
By 苏剑林 | 2010-07-26 | 60456位读者 | 引用已知中心五边形,作五边形
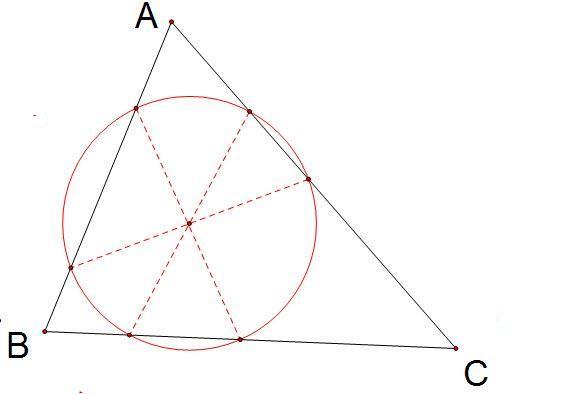
By 苏剑林 | 2010-07-25 | 39684位读者 | 引用神秘的圆——三角形的“六接圆”(添加新方法)
By 苏剑林 | 2010-07-24 | 43384位读者 | 引用《向量》系列——2.曲率半径
By 苏剑林 | 2010-07-18 | 69786位读者 | 引用圆周是如此地和谐与完美,致使数学家和物理学家对它钟爱有加。几何上可以把一条曲线的局部看做一个圆弧,利用圆的性质去研究它(在数学上,曲率半径的倒数就是曲率,曲率越大,曲线越弯曲);物理学家喜欢把一个质点的曲线运动轨迹的局部看做圆周运动,利用圆周运动的方法来描述这种运动。这两种研究方法都告诉了我们,两种不同的“线”在极小的范围内可以等效的,这也为我们对科学进行探究提供了一点指导思想:把未知变已知,以已知看未知。物理学和数学的两种处理方法中,有一点是殊途同归的:那就是看轨迹看成一个圆后,圆的半径是多少?我们首先得求出它。
在数学分析上可以利用微积分的相关知识来推导曲率半径公式,而BoJone则更偏爱物理方法,通过物理和向量知识的结合,推导出曲率半径公式,让BoJone感到“别有一番风味”。
威力巨大的“有向线段”
By 苏剑林 | 2010-06-27 | 25495位读者 | 引用数学魔术——漂亮的近似
By 苏剑林 | 2010-05-29 | 45348位读者 | 引用解答不等式的误区...
By 苏剑林 | 2010-05-02 | 45732位读者 | 引用数值方法解方程之终极算法
By 苏剑林 | 2010-04-04 | 60040位读者 | 引用呵呵,做了一回标题党,可能说得夸张了一点。说是“终极算法”,主要是因为它可以任意提高精度、而且几乎可以应付任何非线性方程(至少理论上是这样),提高精度是已知的迭代式上添加一些项,而不是完全改变迭代式的形式,当然在提高精度的同时,计算量也会随之增大。其理论基础依旧是泰勒级数。
我们考虑方程$x=f(y)$,已知y求x是很容易的,但是已知x求y并不容易。我们考虑把y在$(x_0,y_0)$处展开成x的的泰勒级数。关键是求出y的n阶导数$\frac{d^n y}{dx^n}$。我们记$f^{(n)}(y)=\frac{d^n x}{dy^n}$,并且有
$$\frac{dy}{dx}=\frac{1}{(\frac{dx}{dy})}=f'(y)^{-1}$$









最近评论