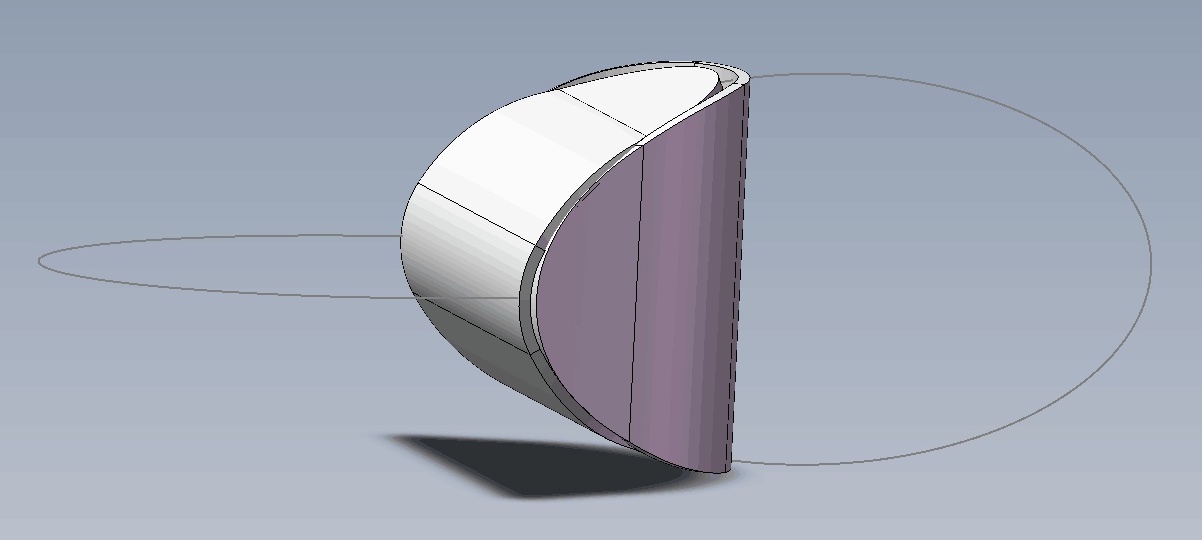
思考:两个椭圆片能粘合成一个立体吗?
By 苏剑林 | 2019-07-21 | 75832位读者 | 引用简述无偏估计和有偏估计
By 苏剑林 | 2019-06-19 | 103552位读者 | 引用对于大多数读者(包括笔者)来说,他们接触到的第一个有偏估计量,应该是方差
\begin{equation}\hat{\sigma}^2_{\text{有偏}} = \frac{1}{n}\sum_{i=1}^n \left(x_i - \hat{\mu}\right)^2,\quad \hat{\mu} = \frac{1}{n}\sum_{i=1}^n x_i\label{eq:youpianfangcha}\end{equation}
然后又了解到对应的无偏估计应该是
\begin{equation}\hat{\sigma}^2_{\text{无偏}} = \frac{1}{n-1}\sum_{i=1}^n \left(x_i - \hat{\mu}\right)^2\label{eq:wupianfangcha}\end{equation}
在很多人的眼里,公式$\eqref{eq:youpianfangcha}$才是合理的,怎么就有偏了?公式$\eqref{eq:wupianfangcha}$将$n$换成反直觉的$n-1$,反而就无偏了?
下面试图用尽量清晰的语言讨论一下无偏估计和有偏估计两个概念。
漫谈重参数:从正态分布到Gumbel Softmax
By 苏剑林 | 2019-06-10 | 334580位读者 | 引用最近在用VAE处理一些文本问题的时候遇到了对离散形式的后验分布求期望的问题,于是沿着“离散分布 + 重参数”这个思路一直搜索下去,最后搜到了Gumbel Softmax,从对Gumbel Softmax的学习过程中,把重参数的相关内容都捋了一遍,还学到一些梯度估计的新知识,遂记录在此。
文章从连续情形出发开始介绍重参数,主要的例子是正态分布的重参数;然后引入离散分布的重参数,这就涉及到了Gumbel Softmax,包括Gumbel Softmax的一些证明和讨论;最后再讲讲重参数背后的一些故事,这主要跟梯度估计有关。
基本概念
重参数(Reparameterization)实际上是处理如下期望形式的目标函数的一种技巧:
\begin{equation}L_{\theta}=\mathbb{E}_{z\sim p_{\theta}(z)}[f(z)]\label{eq:base}\end{equation}
这样的目标在VAE中会出现,在文本GAN也会出现,在强化学习中也会出现($f(z)$对应于奖励函数),所以深究下去,我们会经常碰到这样的目标函数。取决于$z$的连续性,它对应不同的形式:
\begin{equation}\int p_{\theta}(z) f(z)dz\,\,\,\text{(连续情形)}\qquad\qquad \sum_{z} p_{\theta}(z) f(z)\,\,\,\text{(离散情形)}\end{equation}
当然,离散情况下我们更喜欢将记号$z$换成$y$或者$c$。
函数光滑化杂谈:不可导函数的可导逼近
By 苏剑林 | 2019-05-20 | 164118位读者 | 引用一般来说,神经网络处理的东西都是连续的浮点数,标准的输出也是连续型的数字。但实际问题中,我们很多时候都需要一个离散的结果,比如分类问题中我们希望输出正确的类别,“类别”是离散的,“类别的概率”才是连续的;又比如我们很多任务的评测指标实际上都是离散的,比如分类问题的正确率和F1、机器翻译中的BLEU,等等。
还是以分类问题为例,常见的评测指标是正确率,而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联,但它们不是绝对的单调相关关系。换句话说,交叉熵下降了,正确率不一定上升。显然,如果能用正确率的相反数做损失函数,那是最理想的,但正确率是不可导的(涉及到$\text{argmax}$等操作),所以没法直接用。
这时候一般有两种解决方案;一是动用强化学习,将正确率设为奖励函数,这是“用牛刀杀鸡”的方案;另外一种是试图给正确率找一个光滑可导的近似公式。本文就来探讨一下常见的不可导函数的光滑近似,有时候我们称之为“光滑化”,有时候我们也称之为“软化”。
max
后面谈到的大部分内容,基础点就是$\max$操作的光滑近似,我们有:
\begin{equation}\max(x_1,x_2,\dots,x_n) = \lim_{K\to +\infty}\frac{1}{K}\log\left(\sum_{i=1}^n e^{K x_i}\right)\end{equation}
分享:用LaTeX+MathJax画一个三维三阶环方
By 苏剑林 | 2019-03-28 | 22594位读者 | 引用昨天看到数学研发论坛在讨论三维三阶幻方,论坛里的各大牛都已经讨论得差不多了,我也没什么好插话的。然后突发奇想,能不能用纯LaTeX画出一个这样的立体幻方出来?
昨天下午折腾了好一会儿,最后只抛出了个半成品,然后经过论坛的mathe大佬继续完善后,终于成功地画出来了:
$$\begin{array}{ccccccccccc}
& & & & 4 & —& —& — & — & 25 & —& —& — & — & 11
\\
& & & \require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & && &\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} && &&\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} &|
\\
& & 14 & — & — & —& — & 22 & — & — & — & —& 7 & & |
\\
& \require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}& &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & &\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}&&\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} & | & & | \\
24 & — & —& —& — & 1 & —& —& — & — & 18 & & | & & |\\
|& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & &\color{red}{13} &| & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} &\color{red}{27} & | & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & | &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&5\\
|& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & \require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & | & & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} &| & & |&\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} &|\\
|& & \color{red}{8} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}& | &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \color{red}{12} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}& | &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&22&&|\\
|&\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & | &\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}& | &\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} & | &&|\\
15 & — & —& —& — & 3 & — & — & —& —& 21 & & | & &|\\
|& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & & \color{red}{9} &| &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \color{red}{26} &|&\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&|&\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&6\\
|& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}&\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} & &| & &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &&|&&|&\style{display: inline-block; transform: rotate(45deg)}{|}\\
|& &\color{red}{16} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} &|&\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}& \color{red}{8} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}& | & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&17\\
|& \require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}}& & & &|& \require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &&&& | & \require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|}\\
23 & — & — & — & — & 2 & — & — & — & — & 19\\
\end{array}$$
事实上代码里边还内嵌了一些HTML代码,所以不算是严格的纯LaTeX代码,应该说是LaTeX+MathJax的结合。
构造一个显式的、总是可逆的矩阵
By 苏剑林 | 2019-03-01 | 53293位读者 | 引用从《恒等式 det(exp(A)) = exp(Tr(A)) 赏析》一文我们得到矩阵$\exp(\boldsymbol{A})$总是可逆的,它的逆就是$\exp(-\boldsymbol{A})$。问题是$\exp(\boldsymbol{A})$只是一个理论定义,单纯这样写没有什么价值,因为它要把每个$\boldsymbol{A}^n$都算出来。
有没有什么具体的例子呢?有,本文来构造一个显式的、总是可逆的矩阵。
其实思路非常简单,假设$\boldsymbol{x},\boldsymbol{y}$是两个$k$维列向量,那么$\boldsymbol{x}\boldsymbol{y}^{\top}$就是一个$k\times k$的矩阵,我们就来考虑
\begin{equation}\begin{aligned}\exp\left(\boldsymbol{x}\boldsymbol{y}^{\top}\right)=&\sum_{n=0}^{\infty}\frac{\left(\boldsymbol{x}\boldsymbol{y}^{\top}\right)^n}{n!}\\
=&\boldsymbol{I}+\boldsymbol{x}\boldsymbol{y}^{\top}+\frac{\boldsymbol{x}\boldsymbol{y}^{\top}\boldsymbol{x}\boldsymbol{y}^{\top}}{2}+\frac{\boldsymbol{x}\boldsymbol{y}^{\top}\boldsymbol{x}\boldsymbol{y}^{\top}\boldsymbol{x}\boldsymbol{y}^{\top}}{6}+\dots\end{aligned}\end{equation}
恒等式 det(exp(A)) = exp(Tr(A)) 赏析
By 苏剑林 | 2019-02-18 | 90460位读者 | 引用本文的主题是一个有趣的矩阵行列式的恒等式
\begin{equation}\det(\exp(\boldsymbol{A})) = \exp(\text{Tr}(\boldsymbol{A}))\label{eq:main}\end{equation}
这个恒等式在挺多数学和物理的计算中都出现过,笔者都在不同的文献中看到过好几次了。
注意左端是矩阵的指数,然后求行列式,这两步都是计算量非常大的运算;右端仅仅是矩阵的迹(一个标量),然后再做标量的指数。两边的计算量差了不知道多少倍,然而它们居然是相等的!这不得不说是一个神奇的事实。
所以,本文就来好好欣赏一个这个恒等式。
从Wasserstein距离、对偶理论到WGAN
By 苏剑林 | 2019-01-20 | 295149位读者 | 引用2017年的时候笔者曾写过博文《互怼的艺术:从零直达WGAN-GP》,从一个相对通俗的角度来介绍了WGAN,在那篇文章中,WGAN更像是一个天马行空的结果,而实际上跟Wasserstein距离没有多大关系。
在本篇文章中,我们再从更数学化的视角来讨论一下WGAN。当然,本文并不是纯粹地讨论GAN,而主要侧重于Wasserstein距离及其对偶理论的理解。本文受启发于著名的国外博文《Wasserstein GAN and the Kantorovich-Rubinstein Duality》,内容跟它大体上相同,但是删除了一些冗余的部分,对不够充分或者含糊不清的地方作了补充。不管怎样,在此先对前辈及前辈的文章表示致敬。
(注:完整理解本文,应该需要多元微积分、概率论以及线性代数等基础知识。还有,本文确实长,数学公式确实多,但是,真的不复杂、不难懂,大家不要看到公式就吓怕了~)









最近评论