生成扩散模型漫谈(二十一):中值定理加速ODE采样
By 苏剑林 | 2023-12-07 | 152032位读者 |在生成扩散模型的发展史上,DDIM和同期Song Yang的扩散SDE都称得上是里程碑式的工作,因为它们建立起了扩散模型与随机微分方程(SDE)、常微分方程(ODE)这两个数学领域的紧密联系,从而允许我们可以利用SDE、ODE已有的各种数学工具来对分析、求解和拓展扩散模型,比如后续大量的加速采样工作都以此为基础,可以说这打开了生成扩散模型的一个全新视角。
本文我们聚焦于ODE。在本系列的(六)、(十二)、(十四)、(十五)、(十七)等博客中,我们已经推导过ODE与扩散模型的联系,本文则对扩散ODE的采样加速做简单介绍,并重点介绍一种巧妙地利用“中值定理”思想的新颖采样加速方案“AMED”。
欧拉方法 #
正如前面所说,我们已经有多篇文章推导过扩散模型与ODE的联系,所以这里不重复介绍,而是直接将扩散ODE的采样定义为如下ODE的求解:
\begin{equation}\frac{d\boldsymbol{x}_t}{dt} = \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\label{eq:dm-ode}\end{equation}
其中$t\in[0,T]$,初值条件是$\boldsymbol{x}_T$,要返回的结果是$\boldsymbol{x}_0$。原则上我们并不关心$t\in(0,1)$时的中间值$\boldsymbol{x}_t$,只需要最终的$\boldsymbol{x}_0$。为了数值求解,我们还需要选定节点$0=t_0 < t_1 < t_2 < \cdots < t_N = T$,常见的选择是
\begin{equation}t_n=\left(t_1^{1 / \rho}+\frac{n-1}{N-1}\left(t_N^{1 / \rho}-t_1^{1 / \rho}\right)\right)^\rho\end{equation}
其中$\rho > 0$。该形式来自《Elucidating the Design Space of Diffusion-Based Generative Models》(EDM),AMED也沿用了该方案,个人认为节点的选择不算关键要素,因此本文对此不做深究。
最简单的求解器是“欧拉方法”:利用差分近似
\begin{equation}\left.\frac{d\boldsymbol{x}_t}{dt}\right|_{t=t_{n+1}}\approx \frac{\boldsymbol{x}_{t_{n+1}} - \boldsymbol{x}_{t_n}}{t_{n+1} - t_n}\end{equation}
我们可以得到
\begin{equation}\boldsymbol{x}_{t_n}\approx \boldsymbol{x}_{t_{n+1}} - \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_{n+1}}, t_{n+1})(t_{n+1} - t_n)\end{equation}
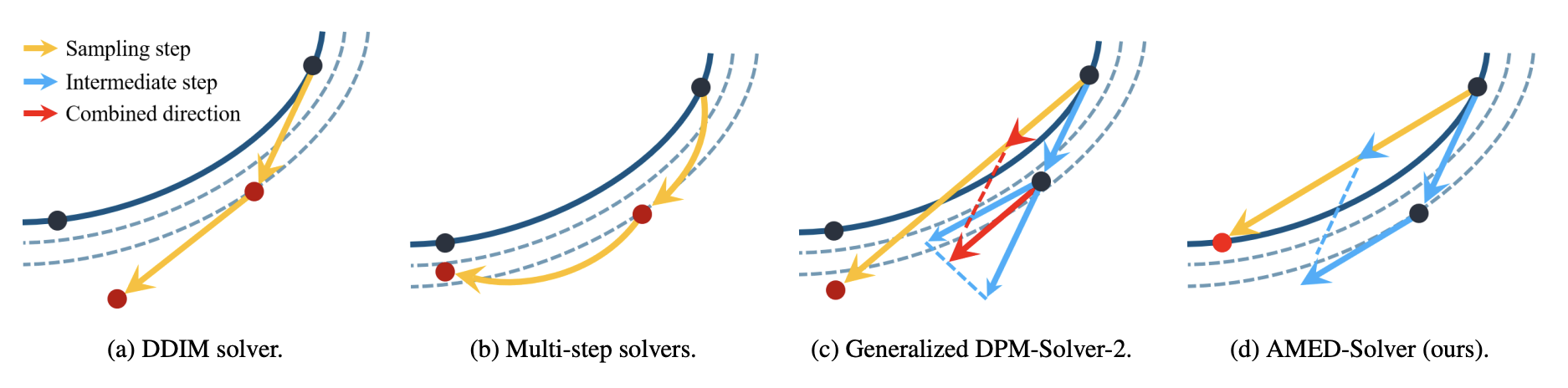
这通常也直接称为DDIM方法,因为是DDIM首先注意到它的采样过程对应于ODE的欧拉法,继而反推出对应的ODE。
高阶方法 #
从数值求解的角度来看,欧拉方法属于一阶近似,特点是简单快捷,缺点是精度差,所以步长不能太小,这意味着单纯利用欧拉法不大可能明显降低采样步数并且保证采样质量。因此,后续的采样加速工作都应用了更高阶的方法。
比如,直觉上差分$\frac{\boldsymbol{x}_{t_{n+1}} - \boldsymbol{x}_{t_n}}{t_{n+1} - t_n}$应该更接近中间点的导数而不是边界的导数,所以右端也换成$t_n$和$t_{n+1}$的平均应该会有更高的精度:
\begin{equation}\frac{\boldsymbol{x}_{t_{n+1}} - \boldsymbol{x}_{t_n}}{t_{n+1} - t_n}\approx \frac{1}{2}\left[\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_n}, t_n) + \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_{n+1}}, t_{n+1})\right]\label{eq:heun-0}\end{equation}
由此我们可以得到
\begin{equation}\boldsymbol{x}_{t_n}\approx \boldsymbol{x}_{t_{n+1}} - \frac{1}{2}\left[\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_n}, t_n) + \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_{n+1}}, t_{n+1})\right](t_{n+1} - t_n) \end{equation}
然而,右端出现了$\boldsymbol{x}_{t_n}$,而我们要做的就是计算$\boldsymbol{x}_{t_n}$,所以这样的等式并不能直接用来迭代,为此,我们用欧拉方法“预估”一下$\boldsymbol{x}_{t_n}$,然后替换掉上式中的$\boldsymbol{x}_{t_n}$:
\begin{equation}\begin{aligned}
\tilde{\boldsymbol{x}}_{t_n}=&\, \boldsymbol{x}_{t_{n+1}} - \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_{n+1}}, t_{n+1})(t_{n+1} - t_n) \\
\boldsymbol{x}_{t_n}\approx&\, \boldsymbol{x}_{t_{n+1}} - \frac{1}{2}\left[\boldsymbol{v}_{\boldsymbol{\theta}}(\tilde{\boldsymbol{x}}_{t_n}, t_n) + \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_{n+1}}, t_{n+1})\right](t_{n+1} - t_n)
\end{aligned}\label{eq:heun}\end{equation}
这就是EDM所用的“Heun方法”,是一种二阶方法。这样每步迭代需要算两次$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$,但精度明显提高,因此可以明显减少迭代步数,总的计算成本是降低的。
二阶方法还有很多变体,比如式$\eqref{eq:heun-0}$的右端我们可以直接换成中间点$t=(t_n+t_{n+1})/2$的函数值,这得到
\begin{equation}\boldsymbol{x}_{t_n}\approx \boldsymbol{x}_{t_{n+1}} - \boldsymbol{v}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{(t_n+t_{n+1})/2}, \frac{t_n+t_{n+1}}{2}\right)(t_{n+1} - t_n) \end{equation}
中间点也有不同的求法,除了代数平均$(t_n+t_{n+1})/2$外,也可以考虑几何平均
\begin{equation}\boldsymbol{x}_{t_n}\approx \boldsymbol{x}_{t_{n+1}} - \boldsymbol{v}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{\sqrt{t_n t_{n+1}}}, \sqrt{t_n t_{n+1}}\right)(t_{n+1} - t_n) \label{eq:dpm-solver-2}\end{equation}
事实上,式$\eqref{eq:dpm-solver-2}$就是DPM-Solver-2的一个特例。
除了二阶方法外,ODE的求解还有不少更高阶的方法,如"Runge-Kutta方法”、“线性多步法”等。然而,不管是二阶方法还是高阶方法,虽然都能一定程度上加速扩散ODE的采样,但由于这些都是“通法”,没有针对扩散模型的背景和形式进行定制,因此很难将采样过程的计算步数降到极致(个位数)。
中值定理 #
至此,本文的主角AMED登场了,其论文《Fast ODE-based Sampling for Diffusion Models in Around 5 Steps》前两天才放到Arxiv,可谓“新鲜滚热辣”。AMED并非像传统的ODE求解器那样一味提高理论精度,而是巧妙地类比了“中值定理”,并加上非常小的蒸馏成本,为扩散ODE定制了高速的求解器。
首先,我们对方程$\eqref{eq:dm-ode}$两端积分,那么可以写出精确的等式:
\begin{equation} \boldsymbol{x}_{t_{n+1}} - \boldsymbol{x}_{t_n} = \int_{t_n}^{t_{n+1}}\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)dt\end{equation}
如果$\boldsymbol{v}$只是一维的标量函数,那么由“积分中值定理”我们可以知道存在点$s_n\in(t_n, t_{n+1})$,使得
\begin{equation}\frac{1}{t_{n+1} - t_n}\int_{t_n}^{t_{n+1}}\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)dt = \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{s_n}, s_n) \end{equation}
很遗憾,中值定理对一般的向量函数并不成立。不过,在$t_{n+1}-t_n$不太大以及一定的假设之下,我们依然可以类比地写出近似
\begin{equation}\frac{1}{t_{n+1} - t_n}\int_{t_n}^{t_{n+1}}\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)dt \approx \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{s_n}, s_n) \end{equation}
于是我们得到
\begin{equation} \boldsymbol{x}_{t_n}\approx \boldsymbol{x}_{t_{n+1}} - \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{s_n}, s_n)(t_{n+1}-t_n)\end{equation}
当然,目前还只是一个形式解,$s_n$和$\boldsymbol{x}_{s_n}$怎么来还未解决。对于$\boldsymbol{x}_{s_n}$,我们依然用欧拉方法进行预估,即$\tilde{\boldsymbol{x}}_{s_n}= \boldsymbol{x}_{t_{n+1}} - \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_{n+1}}, t_{n+1})(t_{n+1} - s_n)$;对于$s_n$,我们则用一个小型的神经网络去估计它:
\begin{equation}s_n = g_{\boldsymbol{\phi}}(\boldsymbol{h}_{t_{n+1}}, t_{n+1})\end{equation}
其中$\boldsymbol{\phi}$是训练参数,$\boldsymbol{h}_{t_{n+1}}$是U-Net模型$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_{n+1}}, t_{n+1})$的中间特征。最后,为了求解参数$\boldsymbol{\phi}$,我们采用蒸馏的思想,预先用步数更多的求解器求出精度更高的轨迹点对$(\boldsymbol{x}_{t_n},\boldsymbol{x}_{t_{n+1}})$,然后最小化估计误差。这就是论文中的AMED-Solver(Approximate MEan-Direction Solver),它具备常规ODE-Solver的形式,但又需要额外的蒸馏成本,然而这点蒸馏成本相比其他蒸馏加速方法又几乎可以忽略不计,所以笔者将它理解为“定制”求解器。
定制一词非常关键,扩散ODE的采样加速研究由来已久,在众多研究人员的贡献加成下,非训练的求解器大概已经走了非常远,但依然未能将采样步数降到极致,除非未来我们对扩散模型的理论理解有进一步的突破,否则笔者不认为非训练的求解器还有显著的提升空间。因此,AMED这种带有少量训练成本的加速度,既是“剑走偏锋”、“另辟蹊径”,也是“应运而生”、“顺理成章”。
实验结果 #
在看实验结果之前,我们首先了解一个名为“NFE”的概念,全称是“Number of Function Evaluations”,说白了就是模型$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$的执行次数,它跟计算量直接挂钩。比如,一阶方法每步迭代的NFE是1,因为只需要执行一次$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$,而二阶方法每一步迭代的NFE是2,AMED-Solver的$g_{\boldsymbol{\phi}}$计算量很小,可以忽略不计,所以AMED-Solver每一步的NFE也算是2。为了实现公平的比较,需要保持整个采样过程中总的NFE不变,来对比不同Solver的效果。
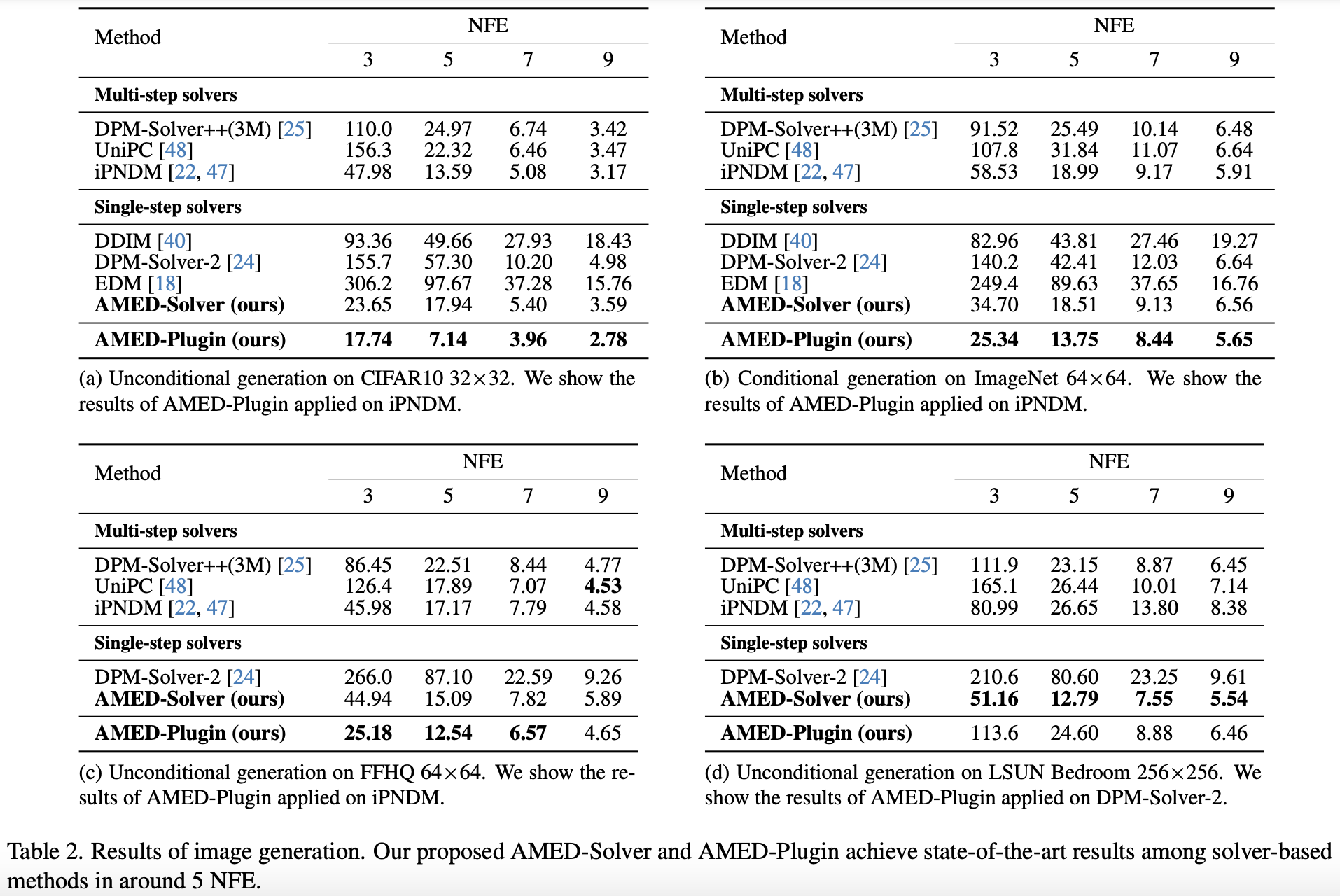
基本的实验结果是原论文的Table 2:
这个表格有几个值得特别留意的地方。第一,在NFE不超过5时,二阶的DPM-Solver、EDM效果还不如一阶的DDIM,这是因为Solver的误差不仅跟阶次有关,还跟步长$t_{n+1}-t_n$有关,大致上的关系就是$\mathcal{O}((t_{n+1}-t_n)^m)$,其中$m$就是“阶”,在总NFE较小时,高阶方法只能取较大的步长,所以实际精度反而更差,从而效果不佳;第二,同样是二阶方法的SMED-Solver,在小NFE时效果取得了全面SOTA,这充分体现了“定制”的重要性;第三,这里的“AMED-Plugin”是原论文提出的将AMED的思想作为其他ODESolver的“插件”的用法,细节更加复杂一些,但取得了更好的效果。
可能有读者会疑问:既然二阶方法每一步迭代都需要2个NFE,那么表格中怎么会出现奇数的NFE?其实,这是因为作者用到了一个名为“AFS(Analytical First Step)”的技巧来减少了1个NFE。该技巧出自《Genie: Higher-order denoising diffusion solvers》,具体是指在扩散模型背景下我们发现$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_N}, t_N)$与$\boldsymbol{x}_{t_N}$非常接近(不同的扩散模型表现可能不大一样,但核心思想都是第一步可以直接解析求解),于是在采样的第一步直接用$\boldsymbol{x}_{t_N}$替代$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_N}, t_N)$,这就省了一个NFE。论文附录的Table 8、Table 9、Table 10也更详尽地评估了AFS对效果的影响,有兴趣的读者可以自行分析。
最后,由于AMED使用了蒸馏的方法来训练$g_{\boldsymbol{\phi}}$,那么也许会有读者想知道它跟其他蒸馏加速的方案的效果差异,不过很遗憾,论文没有提供相关对比。为此我也邮件咨询过作者,作者表示AMED的蒸馏成本是极低的,CIFAR10只需要在单张A100上训练不到20分钟,256大小的图片也只需要在4张A100上训练几个小时,而相比之下其他蒸馏加速的思路需要的时间是数天甚至数十天,因此作者将AMED视为Solver的工作而不是蒸馏的工作。不过作者也表示,后面有机会也尽可能补上跟蒸馏工作的对比。
假设分析 #
前面在讨论中值定理到向量函数的推广时,我们提到“一定的假设之下”,那么这里的假设是什么呢?是否真的成立呢?
不难举出反例证明,即便是二维函数积分中值定理都不恒成立,换言之积分中值定理只在一维函数上成立,这意味着如果高维函数成立积分中值定理,那么该函数所描述的空间轨迹只能是一条直线,也就是说采样过程中所有的$\boldsymbol{x}_{t_0},\boldsymbol{x}_{t_1},\cdots,\boldsymbol{x}_{t_N}$构成一条直线。这个假设自然非常强,实际上几乎不可能成立,但也侧面告诉我们,要想积分中值定理在高维空间尽可能成立,那么采样轨迹要保持在一个尽可能低维的子空间中。
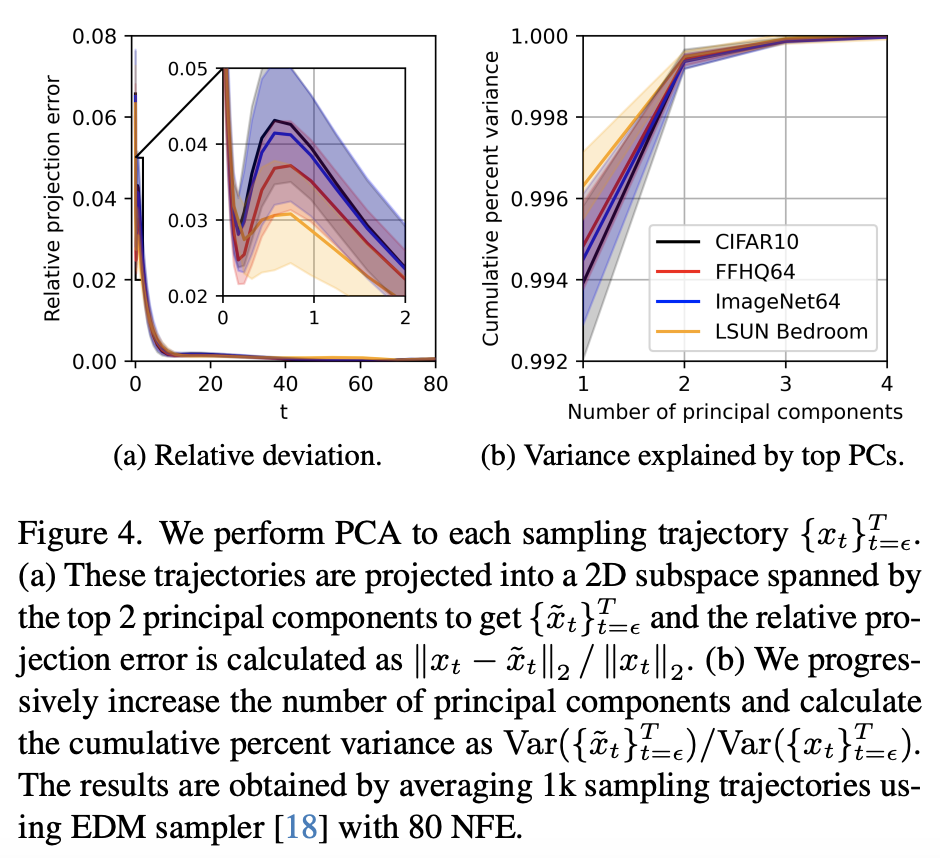
为了验证这一点,论文作者加大了采样步数得到了较为精确的采样轨迹,然后对轨迹做主成分分析,结果如下图所示:
主成分分析的结果显示,只保留top1的主成分,就可以保留轨迹的大部分精度,而同时保留前两个主成本,那么后面的误差几乎可以忽略了,这告诉我们采样轨迹几乎都集中在一个二维子平面上,甚至非常接近这个子平面上的的一个直线,于是在$t_{n+1}-t_n$并不是特别大的时候,扩散模型的高维空间的积分中值定理也近似成立。
这个结果可能会让人比较意外,但事后来看其实也能解释:在《生成扩散模型漫谈(十五):构建ODE的一般步骤(中)》、《生成扩散模型漫谈(十七):构建ODE的一般步骤(下)》我们介绍了先指定$\boldsymbol{x}_T$到$\boldsymbol{x}_0$的“伪轨迹”,然后再构建对应的扩散ODE的一般步骤,而实际应用中,我们所构建的“伪轨迹”都是$\boldsymbol{x}_T$与$\boldsymbol{x}_0$的线性插值(关于$t$可能是非线性的,关于$\boldsymbol{x}_T$和$\boldsymbol{x}_0$则是线性的),于是构建的“伪轨迹”都是直线,这会进一步鼓励真实的扩散轨迹是一条直线,这就解释了主成分分析的结果。
文章小结 #
本文简单回顾了扩散ODE的采样加速方法,并重点介绍了前两天刚发布的一个名为“AMED”的新颖加速采样方案,该Solver类比了积分中值定理来构建迭代格式,以极低的蒸馏成本提高了Solver在低NFE时的表现。
转载到请包括本文地址:https://kexue.fm/archives/9881
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Dec. 07, 2023). 《生成扩散模型漫谈(二十一):中值定理加速ODE采样 》[Blog post]. Retrieved from https://kexue.fm/archives/9881
@online{kexuefm-9881,
title={生成扩散模型漫谈(二十一):中值定理加速ODE采样},
author={苏剑林},
year={2023},
month={Dec},
url={\url{https://kexue.fm/archives/9881}},
}










December 7th, 2023
[...]Read More [...]
December 8th, 2023
这和Progressive Distillation把多步的teacher蒸到少步数的student有什么区别呢....Consistency Model和CONSISTENCY TRAJECTORY MODEL还考虑了求解的一致性,还有一阶段训练的Consistency Training方法,比这种先进的得多啊。
跟纯粹的蒸馏方法相比,蒸馏成本低很多;跟Consistency Training相比的话...我觉得Consistency Training有点丑...
这个方法特点是保留了Solver本身的特性,一次训练完之后,可以改变NFE来实现不同质量的生成结果。从蒸馏的角度来看的话,可以看作是发现了可以用solver来简化student model的结构。
我get到了,蒸馏需要记录下这个中值梯度,而这个solve只需要给出中值位置,用teacher给出梯度,所以solve可以很轻量
不过现有的发展趋势如果像CT一阶段就能训出,只需要很少NFE的类diffusion模型,定制求解器这一方向是不是就没那么重要了呢
我不大确定,Consistency Training虽然是一阶段的,但是它总训练成本跟“正常训练一个DDPM(或者其它ODE扩散模型) + AMED蒸馏”哪个高呢?相比于扩散模型本身的训练成本,AMED蒸馏几乎可以忽略不计的,那么就看Consistency Training跟原本扩散模型的训练成本差距了。
我做的实验是没什么额外成本,甚至有可能通过课程学习大幅降低成本。至于精度损失,又很容易用GAN微调回来
如果考虑GAN微调这种“耍赖”的技术得话,1step是有独特价值的。AMED看起来是至少两次NFE,如果能想办法内置到DDPM,变成1step看起来是不错的思路
AMED跟各种ODE-Solver的方法一样,不改变原始梯度场,而Progressive Distillation,Consistency Distillation等等方法是通过改变一些点的梯度场来加速采样。这是他们之间的本质区别。
其次,AMED的思路也可以推广到更少的NFE,这在理论上没有区别。
AMED可以看做一种微调技术,冻结DDPM引入少量新参数进行蒸馏训练
您好,请问GAN微调是什么意思呢?有没有什么论文中讲解过这个方法呢
December 11th, 2023
这种优化思路会对$g_\phi$的输出或者推理步数会有限制吗?$g_\phi$的输出是否也要限制在区间$(t_n,t_{n+1})$里?如果给定采样步数$N$进行训练,那么推理的时候是不是好像也得固定$N$效果才最好?另外,如果将$(14)$式中的$h_{t_{n+1}}$换成$x_{t_{n+1}}$会对结果产生什么程度的影响吗?鄙人知识尚浅,希望多指教!
$g_{\boldsymbol{\phi}}$只需要输出一个0~1之间的数,然后做变换$t_n + g_{\boldsymbol{\phi}}(t_{n+1}-t_n)$即可(或者其他$[0,1]$到$[t_n,t_{n+1}]$的映射)。
AMED之所以自称Solver,是因为它单次训练之后,还是可以自由地改变NFE以达到不同的生成效果,所以结论是无须固定。
$g_{\boldsymbol{\phi}}$的输入换成$\boldsymbol{x}_{t_{n+1}}$理论上自然没问题,但这可能会让$g_{\boldsymbol{\phi}}$的计算量明显增加(毕竟直接处理原始图片)。
不同的节点选择,中值的位置不是会变化吗,AMED应该依赖于节点吧?如果需要自由变化NFE和节点那么需要$h_{t_{n+1}}, t_{n+1}, t_{n}$三个输入吧,就像CTM那样
对的,AMED需要先选定$t_0,t_1,\cdots,t_N$,然后AMED的作用就是用$g_{\boldsymbol{\phi}}$在$t_i,t_{i+1}$之间插入一个中间点,它的AMED-Plugin也是这样推广到一般的Solver。
所以如果想改变NFE,那么只需要改变$t_0,t_1,\cdots,t_N$中的$N$就行。
那如果想改变N,不就需要重训solve吗
AMED的意思是不需要,一次训练,结果可以改变$N$使用。
那AMED是怎么识别不同的N呢,有N这个输入项吗
可能一个比较说服力的消融实验是随机选一点作为$s_n$的估计,和训练过后的$g_\phi$做对比,不过我在实验部分没看见。
Table 6已经对s_n进行了网格搜索,可以看出中间点的取值对结果影响很大。随机选取情况下,NFE=4对应FID 130+,NFE=6对应FID 50+
这个只能说明选取某一个$r$比较好,况且tab.6的那个$r$不是固定DPM-Solver-2的参数吗?不是随机的吧。我很好奇$s_n$的输出分布,如果不同的$t$的$g_\phi$的输出是一致的,那是不是在推理阶段变成非参,并且保证效果?
不过我还是很疑惑为什么它能自由地改变$N$而保持高性能,我们设$s_n$是基于$N$的前提下采样$(x_{t_n},x_{t_{n+1}})$作为输入和优化目标,那么目标函数应该是 $\min_\phi||x_{t_{n+1}} -v_\theta(x_{t_{n+1}}-v_\theta(x_{t_{n+1}},t_{n+1})(t_{n+1}-g_\phi(h_{t_{n+1}},t_{n+1})),g_\phi(h_{t_{n+1}},t_{n+1})))(t_{n+1}-t_n)-x_{t_n}||$.
一旦$N$变了,那么这个优化目标不就错了吗?中间那一项$v_\theta(x_{t_{n+1}}-v_\theta(x_{t_{n+1}},t_{n+1})(t_{n+1}-g_\phi(h_{t_{n+1}},t_{n+1})),g_\phi(h_{t_{n+1}},t_{n+1})))(t_{n+1}-t_n)$由于$v_\theta$内的函数只与$t_{n+1}$有关,而后面乘积那一项$(t_{n+1}-t_n)$可以视为常数权重,按道理他只会学会一种常数权重的插值模式,但是无论是外推和内插的方式,它对$g_\phi$应该是OOD?我不太理解这一点。如果只是说这么训练的效果就是好,那么我就很怀疑是不是能总结出一个很general的$s_n$,对任意N的采样都能达到一个非常好的效果。
退一步来说,如果不同的$N$均训练需要训练不同的solver,这篇工作的价值是不是就可能没有那么大了?因为不具备迁移性。另外,如果以高阶ODE求解方法预先生成轨迹,那么这个方法的性能的上界应该就是高阶ODE,所以这一篇文章的主要贡献应该就是对高阶ODE进行蒸馏?
1. 随机的结果之前已经回复了。Fig 7已经给了s_n的输出分布。
2. 针对不同的N需要训练不同的$g_\phi$,而$g_\phi$仅有18k参数,储存和推理成本都非常小。此外,由于不同轨迹几何结构类似,还可以让所有轨迹共享权重(time-wise,网络输入只有t),进而只需存下$g_\phi$得到的schedule进行采样即可。这跟以consistency models为代表的蒸馏方法相比,计算量完全不在一个数量级。我们追求的是随着NFE的增加,效果能稳定提升。该性质以consistency models为代表的蒸馏方法不能满足。
3. 上限显然是teacher跑出来的结果。注意teacher可以通过不断增加NFE提升自身的效果。teacher和student可以是相同的solver也可以是不同的solver。该论文的贡献在于,在不改变原始梯度场的情况下(与各种ODE-Solver的方法相同)找approximate mean direction,而非通过改变一些点的梯度场(如Progressive Distillation,Consistency Distillation等)来实现加速采样。
fig 7的一致性我看还是挺高的(浅色的部分应该是方差?),那是不是可以直接用这个训练出来的参数作为每个$s_n$的估计,效果应该也挺不错的?也就是说不同的$x_{t_{n+1}}$并不会影响结果,就像你说的,我们只需要$t_{n+1}$作为网络的唯一输入,那么$t$是离散的话,那么网络只会输出同等量级的答案,所以其实可以不用网络?
大致了解了,谢谢你的解答,这个schedule不知道有没有更好的办法得到,用蒸馏的方法我个人感觉不算太巧妙,不过确实也是一种可行的思路。
December 11th, 2023
我觉得主要诟病的地方是生成大量ODE的GT本身就很耗时,consistency是在线进行单步求解的并不需要生成大量ODE的GT
Section 4.1 Training部分写了训练时间,AMED比consistency models的训练快了几个数量级。
没算生成ODE的时间啊
你似乎没有理解这篇论文的方法,AMED不需要预先生成ODE
见论文Alg1 Generate teacher trajectory
1. 我们计算是总时间,包括你所谓的生成轨迹时间.
2. teacher trajectory是在线生成的,跟consistency models随机取时间点在期望意义下没有区别。总时间主要由iteration和参数量决定。
cifar10单卡生成20k张图就得十多分钟,再加训练时间5-20min这好怪哦
AMED的训练不需要在线生成,如果选择在线生成反而比较不合理
1. 写了A100,不需要5分钟
2. 哪种都无所谓,关键的是计算量很小。这跟consistency models完全不是一个数量级,也不是一类方法。
我在V100上用EDM的源码和环境20步的求解生成20k需要20多分钟,A100的速度一般是2.2倍。所以我看到他报告的时间,就默认他刨去ODE求解了。如果真的包含了,就快得难以置信了。
谢谢您的解答,我还有个疑问是不同的N是一次训练的solver,还是多个分别训练的solve呢
1. EDM默认用Heun solver求解,一步是2NFE。按照EDM源码,num_steps=20时,NFE=39,花20分钟是正常的。AMED中teacher NFE最高为20。十分钟的gap跟consistency models的训练开销相比可以忽略不计。
2. 预测$s_n$也要求知道$t_n$,$t_{n+1}$,所以不同的$N$也是需要训练不同的$g_\phi$。此外可以补充的是,$g_\phi$仅有18k参数,储存和推理成本都非常小。由于不同轨迹几何结构类似,还可以让所有轨迹共享权重(time-wise,网络输入只有$t$),进而只需存下$g_\phi$得到的schedule进行采样即可。
公平比较得让CM只针对一组特定的节点训练,同时冻结DDPM主干使用训练参数量相当的微调技术,再使用一种最先进solve求解。这么比AMDE这个精度不见得有优势。。蒸馏还没有中值定理不存在这种理论上的偏差
哈哈,如此轻量让人有牺牲一些训练成本换取精度的冲动
December 17th, 2023
Bespoke Solvers for Generative Flow Models 也是类似的思想,但参数量更少,期待苏神解析。
感谢推荐,有空读读。
January 4th, 2024
期待苏老师讲解一下一致性模型
September 6th, 2024
请问几种扩散ODE-Solver示意图中深色的实线和虚线分别是什么意思?
实线是理想轨迹,虚线是初始点有所偏离后形成的轨迹。
请问这种偏移是怎么形成的?
大家都是从$\boldsymbol{x}_T$出发,绝对精确地求解方程得到一条准确的轨迹(实线);
不精确的求解方法会得到不精确的$\boldsymbol{x}_{T-1}$,然后从$\boldsymbol{x}_{T-1}$出发,绝对精确地求解方程则得到一条稍微不精确的轨迹(虚线1);
从不精确的$\boldsymbol{x}_{T-1}$出发,不精确的求解方法会得到不精确的$\boldsymbol{x}_{T-2}$,然后从$\boldsymbol{x}_{T-2}$出发,绝对精确地求解方程则得到一条更加不精确的轨迹(虚线2);
依此类推。
September 7th, 2024
您好,我不太理解原文中使用不同的sn形成baseline trajectory和searched trajectory有什么作用,这个表示的意义是什么
不就是想证明精细地搜索$s_n$能取得更好的结果吗
September 10th, 2024
想问一下原文里teacher trajectory那里用M个插值点是怎么进行生成的,不是只需要一个插值点就好了吗,用M个插值点要怎么进行迭代,是用M个插值点都试一下然后选最好的吗
这个我记得好像是用来构建高阶采样器的。
September 24th, 2024
请问为什么AMED-Solver每一步的NFE是2,好像每次只对v计算一次,从公式来看应该怎么理解呢?
首先$\boldsymbol{x}_{t_n}\approx \boldsymbol{x}_{t_{n+1}} - \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{s_n}, s_n)(t_{n+1}-t_n)$,这需要一步$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{s_n}, s_n)$,但别忘了$\boldsymbol{x}_{s_n}$是不知道的,还需要用欧拉法估计一下,即$\boldsymbol{x}_{s_n}\approx \boldsymbol{x}_{t_{n+1}} - \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t_{n+1}}, s_n)(t_{n+1}-s_n)$