Transformer升级之路：10、RoPE是一种β进制编码

对关心如何扩展LLM的Context长度的读者来说，上周无疑是激动人心的一周，开源社区接连不断地出现令人振奋的成果。首先，网友@kaiokendev在他的项目SuperHOT中实验了“位置线性内插”的方案，显示通过非常少的长文本微调，就可以让已有的LLM处理Long Context。几乎同时，Meta也提出了同样的思路，带着丰富的实验结果发表在论文《Extending Context Window of Large Language Models via Positional Interpolation》上。惊喜还远不止此，随后网友@bloc97提出了NTK-aware Scaled RoPE，实现了不用微调就可以扩展Context长度的效果！

以上种种进展，尤其是NTK-aware Scaled RoPE，迫使笔者去重新思考RoPE的含义。经过分析，笔者发现RoPE的构造可以视为一种$\beta$进制编码，在这个视角之下，开源社区的这些进展可以理解为对进制编码编码的不同扩增方式。

进制表示 #

假设我们有一个1000以内（不包含1000）的整数$n$要作为条件输入到模型中，那么要以哪种方式比较好呢？

最朴素的想法是直接作为一维浮点向量输入，然而0～999这涉及到近千的跨度，对基于梯度的优化器来说并不容易优化得动。那缩放到0～1之间呢？也不大好，因为此时相邻的差距从1变成了0.001，模型和优化器都不容易分辨相邻的数字。总的来说，基于梯度的优化器都有点“矫情”，它只能处理好不大不小的输入，太大太小都容易出问题。

所以，为了避免这个问题，我们还需要继续构思新的输入方式。在不知道如何让机器来处理时，我们不妨想想人是怎么处理呢。对于一个整数，比如759，这是一个10进制的三位数，每位数字是0～9。既然我们自己都是用10进制来表示数字的，为什么不直接将10进制表示直接输入模型呢？也就是说，我们将整数$n$以一个三维向量$[a,b,c]$来输入，$a,b,c$分别是$n$的百位、十位、个位。这样，我们既缩小了数字的跨度，又没有缩小相邻数字的差距，代价了增加了输入的维度——刚好，神经网络擅长处理高维数据。

如果想要进一步缩小数字的跨度，我们还可以进一步缩小进制的基数，如使用8进制、6进制甚至2进制，代价是进一步增加输入的维度。

直接外推 #

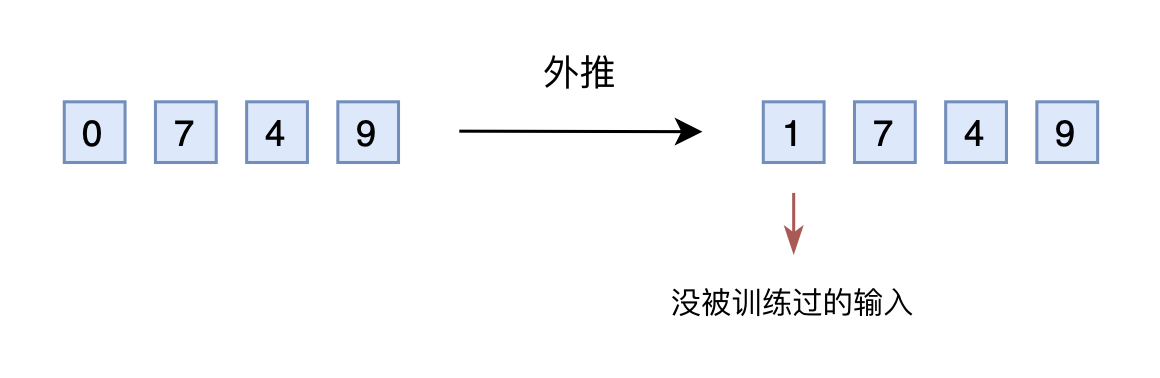
假设我们还是用三维10进制表示训练了模型，模型效果还不错。然后突然来了个新需求，将$n$上限增加到2000以内，那么该如何处理呢？

如果还是用10进制表示的向量输入到模型，那么此时的输入就是一个四维向量了。然而，原本的模型是针对三维向量设计和训练的，所以新增一个维度后，模型就无法处理了。可能有读者想说，为什么不能提前预留好足够多的维度呢？没错，是可以提前预留多几维，训练阶段设为0，推理阶段直接改为其他数字，这就是外推（Extrapolation）。

直接外推

然而，训练阶段预留的维度一直是0，如果推理阶段改为其他数字，效果不见得会好，因为模型对没被训练过的情况不一定具有适应能力。也就是说，由于某些维度的训练数据不充分，所以直接进行外推通常会导致模型的性能严重下降。

线性内插 #

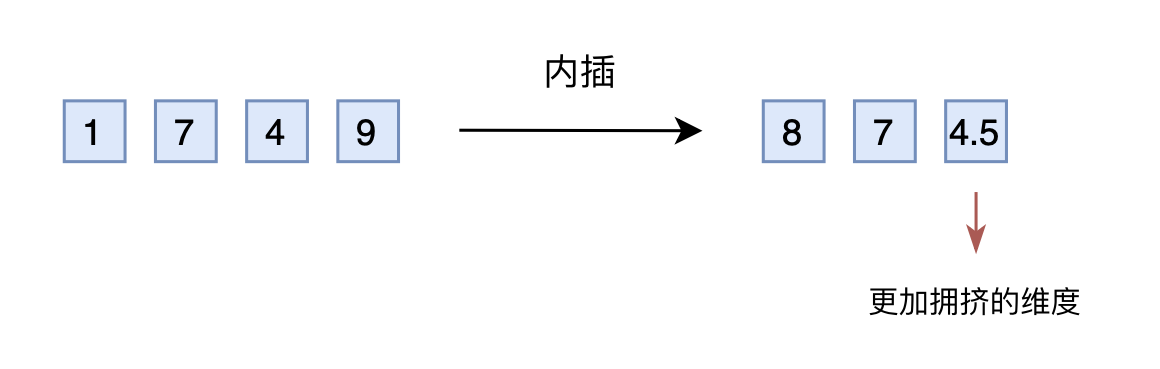
于是，有人想到了将外推改为内插（Interpolation），简单来说就是将2000以内压缩到1000以内，比如通过除以2，1749就变成了874.5，然后转为三维向量[8,7,4.5]输入到原来的模型中。从绝对数值来看，新的$[7,4,9]$实际上对应的是1498，是原本对应的2倍，映射方式不一致；从相对数值来看，原本相邻数字的差距为1，现在是0.5，最后一个维度更加“拥挤”。所以，做了内插修改后，通常都需要微调训练，以便模型重新适应拥挤的映射关系。

线性内插

当然，有读者会说外推方案也可以微调。是的，但内插方案微调所需要的步数要少得多，因为很多场景（比如位置编码）下，相对大小（或许说序信息）更加重要，换句话说模型只需要知道874.5比874大就行了，不需要知道它实际代表什么多大的数字。而原本模型已经学会了875比874大，加之模型本身有一定的泛化能力，所以再多学一个874.5比874大不会太难。

不过，内插方案也不尽完美，当处理范围进一步增大时，相邻差异则更小，并且这个相邻差异变小集中在个位数，剩下的百位、十位，还是保留了相邻差异为1。换句话说，内插方法使得不同维度的分布情况不一样，每个维度变得不对等起来，模型进一步学习难度也更大。

进制转换 #

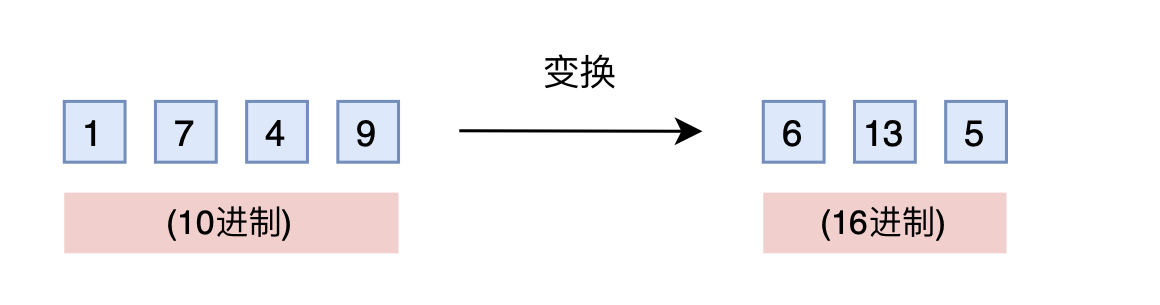
有没有不用新增维度，又能保持相邻差距的方案呢？有，我们也许很熟悉，那就是进制转换！三个数字的10进制编码可以表示0～999，如果是16进制呢？它最大可以表示$16^3 - 1 = 4095 > 1999$。所以，只需要转到16进制，如1749变为$[6,13,5]$，那么三维向量就可以覆盖目标范围，代价是每个维度的数字从0～9变为0～15。

进制转换

仔细想想，就会发现这真是一个绝妙的想法。刚才说到，我们关心的场景主要利用序信息，原来训练好的模型已经学会了$875 > 874$，而在16进制下同样有$875 > 874$，比较规则是一模一样的（模型根本不知道你输入的是多少进制）。唯一担心的是每个维度超过9之后（10～15）模型还能不能正常比较，但事实上一般模型也有一定的泛化能力，所以每个维度稍微往外推一些是没问题的。所以，这个转换进制的思路，甚至可能不微调原来模型也有效！另外，为了进一步缩窄外推范围，我们还可以换用更小的$\left\lceil\sqrt[3]{2000}\right\rceil =13$进制而不是16进制。

接下来我们将会看到，这个进制转换的思想，实际上就对应着文章开头提到的NTK-aware scaled RoPE！

位置编码 #

为了建立起它们的联系，我们先要建立如下结果：

位置$n$的旋转位置编码（RoPE），本质上就是数字$n$的$\beta$进制编码！

看上去可能让人意外，因为两者表面上迥然不同。但事实上，两者的运算有着相同的关键性质。为了理解这一点，我们首先回忆一个10进制的数字$n$，我们想要求它的$\beta$进制表示的（从右往左数）第$m$位数字，方法是
\begin{equation}\left\lfloor\frac{n}{\beta^{m-1}}\right\rfloor\bmod\beta\label{eq:mod}\end{equation}
也就是先除以$\beta^{k-1}$次方，然后求模（余数）。然后再来回忆RoPE，它的构造基础是Sinusoidal位置编码，可以改写为
\begin{equation}\left[\cos\left(\frac{n}{\beta^0}\right),\sin\left(\frac{n}{\beta^0}\right),\cos\left(\frac{n}{\beta^1}\right),\sin\left(\frac{n}{\beta^1}\right),\cdots,\cos\left(\frac{n}{\beta^{d/2-1}}\right),\sin\left(\frac{n}{\beta^{d/2-1}}\right)\right]\label{eq:sinu}\end{equation}
其中，$\beta=10000^{2/d}$。现在，对比式$\eqref{eq:mod}$，式$\eqref{eq:sinu}$是不是也有一模一样的$\frac{n}{\beta^{m-1}}$？至于模运算，它的最重要特性是周期性，式$\eqref{eq:sinu}$的$\cos,\sin$是不是刚好也是周期函数？所以，除掉取整函数这个无关紧要的差异外，RoPE（或者说Sinusoidal位置编码）其实就是数字$n$的$\beta$进制编码！

建立起这个联系后，前面几节讨论的整数$n$的扩增方案，就可以对应到文章开头的各种进展上了。其中，直接外推方案就是啥也不改，内插方案就是将$n$换成$n/k$，其中$k$是要扩大的倍数，这就是Meta的论文所实验的Positional Interpolation，里边的实验结果也证明了外推比内插确实需要更多的微调步数。

至于进制转换，就是要扩大$k$倍表示范围，那么原本的$\beta$进制至少要扩大成$\beta (k^{2/d})$进制（式$\eqref{eq:sinu}$虽然是$d$维向量，但$\cos,\sin$是成对出现的，所以相当于$d/2$位$\beta$进制表示，因此要开$d/2$次方而不是$d$次方），或者等价地原来的底数$10000$换成$10000k$，这基本上就是NTK-aware Scaled RoPE。跟前面讨论的一样，由于位置编码更依赖于序信息，而进制转换基本不改变序的比较规则，所以NTK-aware Scaled RoPE在不微调的情况下，也能在更长Context上取得不错的效果。

追根溯源 #

可能有读者好奇，这跟NTK有什么关系呢？NTK全称是“Neural Tangent Kernel”，我们之前在《从动力学角度看优化算法（七）：SGD ≈ SVM？》也稍微涉及过。要说上述结果跟NTK的关系，更多的是提出者的学术背景缘故，提出者对《Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains》等结果比较熟悉，里边利用NTK相关结果证明了神经网络无法直接学习高频信号，解决办法是要将它转化为Fourier特征——其形式就跟式$\eqref{eq:mod}$的Sinusoidal位置编码差不多。

所以，提出者基于NTK相关结果的直觉，推导了NTK-aware Scaled RoPE。笔者向提出者请教过他的推导，其实他的推导很简单，就是把外推和内插结合起来——高频外推、低频内插。具体来说，式$\eqref{eq:sinu}$最低频是$\frac{n}{\beta^{d/2-1}}$项，引入参数$\lambda$变为$\frac{n}{(\beta\lambda)^{d/2-1}}$，让它跟内插一致，即
\begin{equation}\frac{n}{(\beta\lambda)^{d/2-1}} = \frac{n/k}{\beta^{d/2-1}}\end{equation}
那么解得$\lambda=k^{2/(d-2)}$。至于最高频是$\frac{n}{\beta}$项，引入$\lambda$后变为$\frac{n}{\beta\lambda}$，由于$d$通常很大，$\lambda$很接近1，所以它还是接近于$\frac{n}{\beta}$，即等价于外推。

所以这样的方案简单巧妙地将外推和内插结合了起来。另外，由于$d$比较大（BERT是64，LLAMA是128），$k^{2/(d-2)}$跟$k^{2/d}$差别不大，所以它跟笔者基于进制思想提出的$k^{2/d}$解是基本一致的。还有，从提出者这个思想来看，任意能实现“高频外推、低频内插”的方案都是可以的，并非只有上述引入$\lambda$的方案，这个读者可以亲自尝试一下。

个人测试 #

作为号称不用微调就可以增加LLM的Context长度的方案，笔者第一次看到NTK-aware Scaled RoPE时，也感到很震惊，并且迫不及待地去测试它。毕竟根据《Transformer升级之路：9、一种全局长度外推的新思路》的经验，在笔者所偏爱的“GAU+Post Norm”组合上，很多主流的方案都失效了，那么这个方法又如何？

当$k$取8时，对比结果如下（关于“重复”与“不重复”的区别，可以参考这里）
\begin{array}{c|cc}
\hline
\text{测试长度} & 512(\text{训练}) & 4096(\text{重复}) & 4096(\text{不重复})\\
\hline
\text{Baseline} & 49.41\% & 24.17\% & 23.16\% \\
\text{Baseline-}\log n & 49.40\% & 24.60\% & 24.02\% \\
\hline
\text{PI-RoPE} & 49.41\% & 15.04\% & 13.54\% \\
\text{PI-RoPE-}\log n & 49.40\% & 14.99\% & 16.51\% \\
\hline
\text{NTK-RoPE} & 49.41\% & 51.28\% & 39.27\% \\
\text{NTK-RoPE-}\log n & 49.40\% & 61.71\% & 43.75\% \\
\hline
\end{array}
以上报告的都是没有经过长文本微调的结果，其中Baseline就是外推，PI（Positional Interpolation）就是Baseline基础上改内插，NTK-RoPE就是Baseline基础上改NTK-aware Scaled RoPE。带$\log n$的选项，是指预训练时加入了《从熵不变性看Attention的Scale操作》中的scale，考虑这个变体是因为笔者觉得NTK-RoPE虽然解决了RoPE的长度泛化问题，但没有解决注意力不集中问题。

表格的实验结果完全符合预期：

1、直接外推的效果不大行；

2、内插如果不微调，效果也很差；

3、NTK-RoPE不微调就取得了非平凡（但有所下降）的外推结果；

4、加入$\log n$来集中注意力确实有帮助。

所以，NTK-RoPE成功地成为目前第二种笔者测试有效的不用微调就可以扩展LLM的Context长度的方案（第一种自然是NBCE），再次为提出者的卓越洞察力点赞！更加值得高兴的是，NTK-RoPE在“重复”外推上比“不重复”外推效果明显好，表明这样修改之后是保留了全局依赖，而不是单纯将注意力局部化。

写在最后 #

本文从$\beta$进制编码的角度理解RoPE，并借此介绍了目前开源社区关于Long Context的一些进展，其中还包含了一种不用微调就可以增加Context长度的修改方案。

仅仅一周，开源社区的Long Context进展就让人应接不暇，也大快人心，以至于网友@ironborn123评论道

上周看上去是插值器的报复:) OpenClosedAI最好小心了

转载到请包括本文地址：https://kexue.fm/archives/9675

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。