RSGAN:对抗模型中的“图灵测试”思想
By 苏剑林 | 2018-10-22 | 163352位读者 |这两天无意间发现一个非常有意义的工作,称为“相对GAN”,简称RSGAN,来自文章《The relativistic discriminator: a key element missing from standard GAN》,据说该文章还得到了GAN创始人Goodfellow的点赞。这篇文章提出了用相对的判别器来取代标准GAN原有的判别器,使得生成器的收敛更为迅速,训练更为稳定。
可惜的是,这篇文章仅仅从训练和实验角度对结果进行了论述,并没有进行更深入的分析,以至于不少人觉得这只是GAN训练的一个trick。但是在笔者来看,RSGAN具有更为深刻的含义,甚至可以看成它已经开创了一个新的GAN流派。所以,笔者决定对RSGAN模型及其背后的内涵做一个基本的介绍。不过需要指出的是,除了结果一样之外,本文的介绍过程跟原论文相比几乎没有重合之处。
“图灵测试”思想 #
SGAN #
SGAN就是标准的GAN(Standard GAN)。就算没有做过GAN研究的读者,相信也从各种渠道了解到GAN的大概原理:“造假者”不断地进行造假,试图愚弄“鉴别者”;“鉴别者”不断提高鉴别技术,以分辨出真品和赝品。两者相互竞争,共同进步,直到“鉴别者”无法分辨出真、赝品了,“造假者”就功成身退了。
在建模时,通过交替训练实现这个过程:固定生成器,训练一个判别器(二分类模型),将真实样本输出1,将伪造样本输出0;然后固定判别器,训练生成器让伪造样本尽可能输出1,后面这一步不需要真实样本参与。
问题所在 #
然而,这个建模过程似乎对判别器的要求过于苛刻了,因为判别器是孤立运作的:训练生成器时,真实样本没有参与,所以判别器必须把关于真实样本的所有属性记住,这样才能指导生成器生成更真实的样本。
在生活实际中,我们并不是这样做的,所谓“没有对比就没有伤害,没有伤害就没有进步”,我们很多时候是根据真、赝品的对比来分辨的。比如识别一张假币,可能需要把它跟一张真币对比一下;识别山寨手机,只需要将它跟正版手机对比一下就行了;等等。类似地,如果要想把赝品造得更真,那么需要把真品放在一旁不断地进行对比改进,而不是单单凭借“记忆”中的真品来改进。
“对比”能让我们更容易识别出真、赝品出来,从而更好地制造赝品。而在人工智能领域,我们知道有非常著名的“图灵测试”,指的是测试者在无法预知的情况下同时跟机器人和人进行交流,如果测试者无法成功分别出人和机器人,那么说明这个机器人已经(在某个方面)具有人的智能了。“图灵测试”也强调了对比的重要性,如果机器人和人混合起来后就无法分辨了,那么说明机器人已经成功了。
接下来我们将会看到,RSGAN就是基于“图灵测试”的思想的:如果鉴别器无法鉴别出混合的真假图片,那么生成器就成功了;而为了生成更好的图片,生成器也需要直接借助于真实图片。
RSGAN基本框架 #
SGAN分析 #
首先,我们来回顾一下标准的GAN的流程。设真实样本分布为$\tilde{p}(x)$,伪造样本分布为$q(x)$,那么固定生成器后,我们来优化判别器$T(x)$:
\begin{equation}\min_{T}-\mathbb{E}_{x\sim \tilde{p}(x)}[\log \sigma(T(x))] - \mathbb{E}_{x\sim q(x)}[\log(1-\sigma(T(x)))]\label{eq:sgan-d}\end{equation}
这里的$\sigma$就是sigmoid激活函数。然后固定判别器,我们优化生成器$G(z)$:
\begin{equation}\min_{G}\mathbb{E}_{x=G(z),z\sim q(z)}[h(T(x))]\label{eq:sgan-g}\end{equation}
注意这里我们有个不确定$h$,我们马上就来分析它。
从$\eqref{eq:sgan-d}$我们可以解出判别器的最优解满足(后面有补充证明)
\begin{equation}\frac{\tilde{p}(x)}{q(x)}=\frac{\sigma(T(x))}{1 - \sigma(T(x))} = e^{T(x)}\end{equation}
代入$\eqref{eq:sgan-g}$,可以发现结果为
\begin{equation}\min_{G}\mathbb{E}_{x=G(z),z\sim q(z)}\left[h\left(\log\frac{\tilde{p}(x)}{q(x)}\right)\right]=\min_{G}\int q(x)\left[h\left(\log\frac{\tilde{p}(x)}{q(x)}\right)\right]dx
\end{equation}
写成最后一个等式,是因为只需要设$f(t)=h(\log(t))$,就能够看出它具有f散度的形式。也就是说,最小化$\eqref{eq:sgan-g}$就是在最小化对应的f散度。关于f散度,可以参数我之前写的《f-GAN简介:GAN模型的生产车间》。f散度中的f的本质要求是$f$是一个凸函数,所以只需要选择$h$使得$h(\log(t))$为凸函数就行。最简单的情况是$h(t)=-t$,对应$h(\log(t))=-\log t$为凸函数,这时候$\eqref{eq:sgan-g}$为
\begin{equation}\min_{G}\mathbb{E}_{x=G(z),z\sim q(z)}[-T(x)]\end{equation}
类似的选择有很多,比如当$h(t)=-\log \sigma(t)$时,$h(\log(t))=\log \left(1+\frac{1}{t}\right)$也是凸函数($t > 0$时),所以
\begin{equation}\min_{G}\mathbb{E}_{x=G(z),z\sim q(z)}[-\log\sigma(T(x))]\end{equation}
也是一个合理的选择,它便是GAN常用的生成器loss之一。类似地还有$h(t)=\log(1-\sigma(t))$,这些选择就不枚举了。
RSGAN目标 #
这里,我们先直接给出RSGAN的优化目标:固定生成器后,我们来优化判别器$T(x)$:
\begin{equation}\min_{T}-\mathbb{E}_{x_r\sim \tilde{p}(x), x_f\sim q(x)}[\log \sigma(T(x_r)-T(x_f))]\label{eq:rsgan-d}\end{equation}
这里的$\sigma$就是sigmoid激活函数。然后固定判别器,我们优化生成器$G(z)$:
\begin{equation}\min_{G}\mathbb{E}_{x_r\sim \tilde{p}(x), x_f=G(z),z\sim q(z)}[h(T(x_f) - T(x_r))]\label{eq:rsgan-g}\end{equation}
跟SGAN一样,我们这里保留了一般的$h$,$h$的要求跟前面的SGAN的讨论一致。而RSGAN原论文的选择是
\begin{equation}\min_{G}-\mathbb{E}_{x_r\sim \tilde{p}(x), x_f=G(z),z\sim q(z)}[\log\sigma(T(x_f) - T(x_r))]\end{equation}
看上去就是把SGAN的判别器的两项换成一个相对判别器了,相关的分析结果有什么变化呢?
理论结果 #
通过变分法(后面有补充证明)可以得到,$\eqref{eq:rsgan-d}$的最优解为
\begin{equation}\frac{\tilde{p}(x_r)q(x_f)}{\tilde{p}(x_f)q(x_r)}=\frac{\sigma(T(x_r)-T(x_f))}{\sigma(T(x_f)-T(x_r))}=e^{T(x_r)-T(x_f)}\end{equation}
代入到$\eqref{eq:rsgan-g}$,结果是
\begin{equation}\begin{aligned}&\min_{G}\mathbb{E}_{x_r\sim \tilde{p}(x), x_f=G(z),z\sim q(z)}\left[h\left(\log\frac{\tilde{p}(x_f)q(x_r)}{\tilde{p}(x_r)q(x_f)}\right)\right]\\
=&\min_{G}\iint \tilde{p}(x_r)q(x_f)\left[h\left(\log\frac{\tilde{p}(x_f)q(x_r)}{\tilde{p}(x_r)q(x_f)}\right)\right] dx_r dx_f\end{aligned}\label{eq:rsgan-gg}\end{equation}
这个结果便是整个RSGAN的精华所在了,它优化的是$\tilde{p}(x_r)q(x_f)$与$\tilde{p}(x_f)q(x_r)$的f散度!
这是什么意思呢?它就是说,假如我从真实样本采样一个$x_r$出来,从伪造样本采样一个$x_f$出来,然后将它们交换一下,把假的当成真,真的当成假,那么还能分辨出来吗?换言之:$\tilde{p}(x_f)q(x_r)$有大变化吗?
假如没有什么变化,那就说明真假样本已经无法分辨了,训练成功,假如还能分辨出来,说明还需要借助真实样本来改善伪造样本。所以,式$\eqref{eq:rsgan-gg}$就是RSGAN中的“图灵测试”思想的体现:打乱了数据,是否还能分辨出来?
模型效果分析 #
作者在原论文中还提出了一个RaSGAN,a是average的意思,就是用整个batch的平均来代替单一的真/伪样本。但我觉得这不是一个特别优雅的做法,而且论文也表明RaSGAN的效果并非总是比RSGAN要好,所以这就不介绍了,有兴趣的读者看看原论文即可。
至于效果,论文中的效果列表显示,RSGAN在不少任务上都提升了模型的生成质量,但这并非总是这样,平均而言有轻微的提升吧。作者特别指出的是RSGAN能够加快生成器的训练速度,我个人也实验了一下,比SGAN、SNGAN都要快一些。
我的参考代码:
https://github.com/bojone/gan/blob/master/keras/rsgan_sn_celeba.py
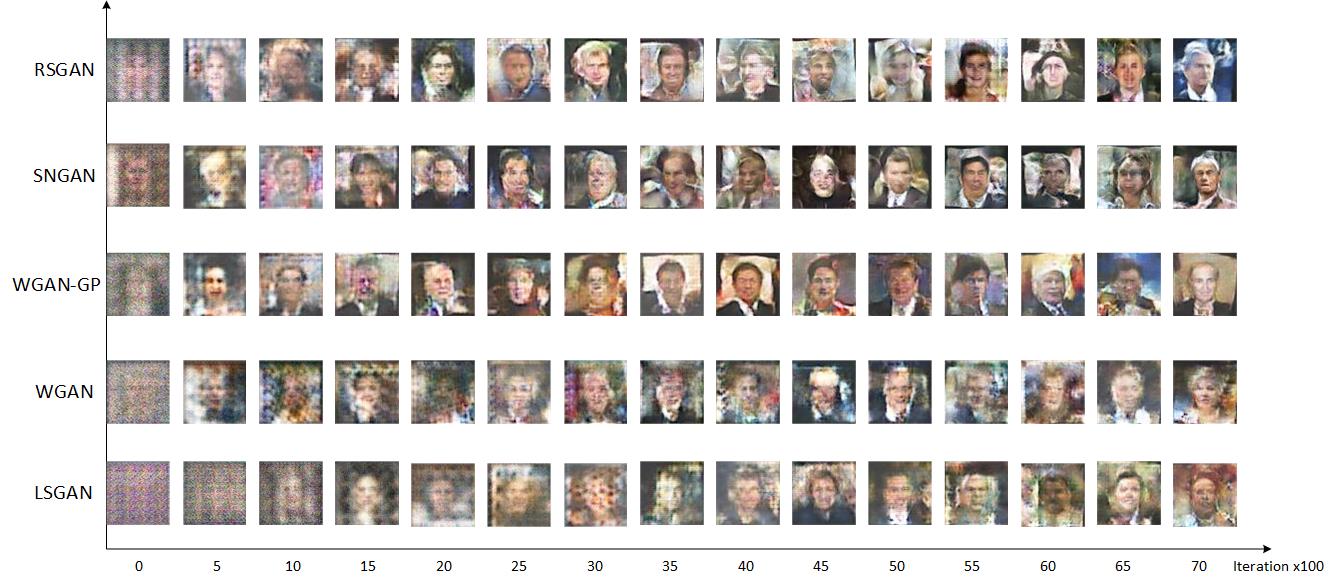
借用MingtaoGuo的一张图来对比RSGAN的收敛速度:
从直观来看,RSGAN更快是因为在训练生成器时也借用了真实样本的信息,而不仅仅通过判别器的“记忆”;从理论上看,通过$T(x_r)$、$T(x_f)$作差的方式,使得判别器只依赖于它们的相对值,从而简单地改善了判别器$T$可能存在的偏置情况,使得梯度更加稳定。甚至我觉得,把真实样本也引入到生成器的训练中,有可能(没仔细证明)提升伪造样本的多样性,因为有了各种真实样本来对比,模型如果只生成单一样本,也很难满足判别器的对比判别标准。
相关话题讨论 #
简单总结 #
总的来说,我觉得RSGAN是对GAN的改进是从思想上做了改变的,也许RSGAN的作者也没有留意到这一点。
我们经常说,WGAN是GAN之后的一大突破,这没错,但这个突破是理论上的,而在思想上还是一样,都是在减少两个分布的距离,只不过以前用JS散度可能有各种问题,而WGAN换用了Wasserstein距离。我觉得RSGAN更像是一种思想上的突破——转化为真假样本混淆之后的分辨——尽管效果未必有大的进步。(当然你要是说大家最终的效果都是拉近了分布距离,那我也没话说^_^)
RSGAN的一些提升是容易重现的,当然由于不是各种任务都有提升,所以也有人诟病这不过是GAN训练的一个trick。这些评论见仁见智吧,不妨碍我对这篇论文的赞赏和研究。
对了,顺便说一下,作者Alexia Jolicoeur-Martineau是犹太人总医院(Jewish General Hospital)的一名女生物统计学家,论文中的结果是她只用一颗1060跑出来的(出处在这里)。我突然也为我只有一颗1060感到自豪了...(然而我有1060但我并没有paper~)
延伸讨论 #
最后胡扯一些延伸的话题。
首先,可以留意到,WGAN的判别器loss本身就是两项的差的形式,也就是说WGAN的判别器就是一个相对判别器,作者认为这是WGAN效果好的重要原因。
这样看上去WGAN跟RSGAN本身就有一些交集,但我有个更进一步的想法,就是基于$\tilde{p}(x_r)q(x_f)$与$\tilde{p}(x_f)q(x_r)$的比较能否完全换用Wasserstein距离来进行?我们知道WGAN的生成器训练目标也是跟真实样本没关系的,怎么更好地将真实样本的信息引入到WGAN的生成器中去?
还有一个问题,就是目前作差仅仅是判别器最后输出的标量作差,那么能不能是判别器的某个隐藏层作差,然后算个mse或者再接几层神经网络?。总之,我觉得这个模型的事情应该还没完...
补充证明 #
1、$\eqref{eq:sgan-d}$的最优解
\begin{equation}\begin{aligned}&-\mathbb{E}_{x\sim \tilde{p}(x)}[\log \sigma(T(x))] - \mathbb{E}_{x\sim q(x)}[\log(1-\sigma(T(x)))]\\
=&-\int \Big(\tilde{p}(x) \log \sigma(T(x)) + q(x) \log(1-\sigma(T(x))) \Big)dx\end{aligned}\end{equation}
变分用$\delta$表示,跟微分基本一样:
\begin{equation}\begin{aligned}&\delta \int \Big(\tilde{p}(x) \log \sigma(T(x)) + q(x) \log(1-\sigma(T(x))) \Big)dx\\
=& \int \left(\tilde{p}(x) \frac{\delta \sigma(T(x))}{\sigma(T(x))} + q(x) \frac{-\delta \sigma(T(x))}{1-\sigma(T(x))} \right)dx\\
=& \int \left(\tilde{p}(x) \frac{1}{\sigma(T(x))} - q(x) \frac{1}{1-\sigma(T(x))} \right)\delta \sigma(T(x)) dx
\end{aligned}\end{equation}
极值在变分为0时取到,而$\delta \sigma(T(x))$代表任意增量,所以如果上式恒为0,意味着括号内的部分恒为0,即
\begin{equation}\tilde{p}(x) \frac{1}{\sigma(T(x))} = q(x) \frac{1}{1-\sigma(T(x))}\end{equation}2、$\eqref{eq:rsgan-d}$的最优解
\begin{equation}\begin{aligned}&-\mathbb{E}_{x_r\sim \tilde{p}(x), x_f\sim q(x)}[\log \sigma(T(x_r)-T(x_f))]\\
=&-\iint \tilde{p}(x_r)q(x_f)\log \sigma(T(x_r)-T(x_f)) dx_r dx_f\end{aligned}\end{equation}
变分上式:
\begin{equation}\begin{aligned}&\delta \iint \tilde{p}(x_r)q(x_f)\log \sigma(T(x_r)-T(x_f)) dx_r dx_f\\
=& \iint \tilde{p}(x_r)q(x_f)\frac{\delta \sigma(T(x_r)-T(x_f))}{\sigma(T(x_r)-T(x_f))} dx_r dx_f\quad[\text{接下来利用}\sigma'(x)=\sigma(x)\sigma(-x)]\\
=& \iint \tilde{p}(x_r)q(x_f)\sigma(T(x_f)-T(x_r)) \times (\delta T(x_r)-\delta T(x_f)) dx_r dx_f\\
=& \iint \tilde{p}(x_r)q(x_f)\sigma(T(x_f)-T(x_r)) \delta T(x_r) dx_r dx_f \quad[\text{接下来交换第二项的}x_r,x_f]\\
&\qquad - \iint \tilde{p}(x_r)q(x_f)\sigma(T(x_f)-T(x_r)) \delta T(x_f) dx_r dx_f\\
=& \iint \tilde{p}(x_r)q(x_f)\sigma(T(x_f)-T(x_r)) \delta T(x_r) dx_r dx_f \\
&\qquad - \iint \tilde{p}(x_f)q(x_r)\sigma(T(x_r)-T(x_f)) \delta T(x_r) dx_f dx_r\\
=& \iint \Big[\tilde{p}(x_r)q(x_f)\sigma(T(x_f)-T(x_r)) \\
&\qquad\qquad- \tilde{p}(x_f)q(x_r)\sigma(T(x_r)-T(x_f))\Big] \delta T(x_r) dx_r dx_f
\end{aligned}\end{equation}
极值在变分为0时取到,所以方括号内的部分恒为0,即
\begin{equation}\tilde{p}(x_r)q(x_f)\sigma(T(x_f)-T(x_r))=\tilde{p}(x_f)q(x_r)\sigma(T(x_r)-T(x_f))\end{equation}
转载到请包括本文地址:https://kexue.fm/archives/6110
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Oct. 22, 2018). 《RSGAN:对抗模型中的“图灵测试”思想 》[Blog post]. Retrieved from https://kexue.fm/archives/6110
@online{kexuefm-6110,
title={RSGAN:对抗模型中的“图灵测试”思想},
author={苏剑林},
year={2018},
month={Oct},
url={\url{https://kexue.fm/archives/6110}},
}










October 22nd, 2018
公式不支持
嗯,小程序里边目前还没有想到好办法~
October 22nd, 2018
gan在nlp上应用如何哈?
October 23rd, 2018
式子16是不是有些问题?感觉利用sigmoid的导数时,多了一个负号。
不过不影响最终结果
哪里多了一个负号呢?第几行?
在利用sigmoid的导数时,应该是xr的变分减去xf的变分
式子16的第二行到第三行
是的,你是对的,已经改过来了。我有点想当然了~
写得很赞,打call
October 24th, 2018
请问16式为什么可以交换 $x_r$ 和 $x_f$
$x_r,x_f$只不过是两个积分变量的记号,交换之后不改变结果呀。好比$\int_0^1 xdx = \int_0^1 tdt$,这就是把$x$换成$t$。
October 25th, 2018
请教一下,公式1到公式2,优化完鉴定器后,生成器的h函数为什么可以设置为其他函数,而不是生成器对应的log函数?
文中已经证明了呀,$(1)$式实际上在想办法估计$\tilde{p}(x)$,估计完之后,就可以拉近$q(x)$和$\tilde{p}(x)$的距离了,这个距离可以是任意的$f$散度,不一定局限于KL散度或者是JS散度,从而我们可以灵活选择$h$。
October 29th, 2018
您好,(2)式中$x\tidle G(x)$而(3)式子中x是空间的均匀采样,这可以在(4)式中直接带入吗?
$(3)$式为什么是空间均匀采样?
November 6th, 2018
看了你的论文,图灵测试思想让人眼前一亮,太有意思了
November 6th, 2018
是否能在cifar-10上面做实验,看看与SN-GAN、SA-GAN的效果对比?
最新的论文版本已经在cifar-10做了简单实验,不过没有完整地对比。
November 6th, 2018
Progressive growing of gans for improved quality, stability, and variation
这篇ICLR 2018的文章,已经在CELEBA HQ dataset上做出了非凡的效果,你可以试试把它的思想加上你的思想,看看最后的实验结果,这样才能证明你的方法的有效性。
另外,这篇文章的附录里也有在CIFAR10上面做的实验,用的metric是Inception Score。
感谢你的关注和建议,我可能跑不起来PGGAN的模型了(苦笑)。
其实我的结果只想证明,在同样的技术手段并且大家都work的情况下,T-GANs能比SGANs和WGANs收敛更快、更稳甚至更好,论文上的实验大体能证明这一点。
我比较关注的点是:如何用更自然的、更符合理论解释的、更少超参的方式训练出一个比较好的GAN模型。比如我基于T-GANs得到了一个新的正则方案(还没有写在论文中),这个正则方案表明能较好地稳定判别器,同时几乎没有超参数,而且不像“梯度惩罚”那样感觉是一种拼凑的结果。
欢迎后续关注。
Nice,期待大作
November 6th, 2018
T(xr, xf) = D(E(xr) − E(xf))
两个Encoder的结果直接相减是一种暴力的方式;把两个拼接起来,再送入判别器可能效果会更好。
其实相减能起到更好的正则作用,后面我会进一步写文章探讨这个问题。