变分自编码器(四):一步到位的聚类方案
By 苏剑林 | 2018-09-17 | 485246位读者 |由于VAE中既有编码器又有解码器(生成器),同时隐变量分布又被近似编码为标准正态分布,因此VAE既是一个生成模型,又是一个特征提取器。在图像领域中,由于VAE生成的图片偏模糊,因此大家通常更关心VAE作为图像特征提取器的作用。提取特征都是为了下一步的任务准备的,而下一步的任务可能有很多,比如分类、聚类等。本文来关心“聚类”这个任务。
一般来说,用AE或者VAE做聚类都是分步来进行的,即先训练一个普通的VAE,然后得到原始数据的隐变量,接着对隐变量做一个K-Means或GMM之类的。但是这样的思路的整体感显然不够,而且聚类方法的选择也让我们纠结。本文介绍基于VAE的一个“一步到位”的聚类思路,它同时允许我们完成无监督地完成聚类和条件生成。
理论 #
一般框架 #
回顾VAE的loss(如果没印象请参考《变分自编码器(二):从贝叶斯观点出发》):
$$KL\Big(p(x,z)\Big\Vert q(x,z)\Big) = \iint p(z|x)\tilde{p}(x)\ln \frac{p(z|x)\tilde{p}(x)}{q(x|z)q(z)} dzdx\tag{1}$$
通常来说,我们会假设$q(z)$是标准正态分布,$p(z|x),q(x|z)$是条件正态分布,然后代入计算,就得到了普通的VAE的loss。
然而,也没有谁规定隐变量一定是连续变量吧?这里我们就将隐变量定为$(z, y)$,其中$z$是一个连续变量,代表编码向量;$y$是离散的变量,代表类别。直接把$(1)$中的$z$替换为$(z,y)$,就得到
$$KL\Big(p(x,z,y)\Big\Vert q(x,z,y)\Big) = \sum_y \iint p(z,y|x)\tilde{p}(x)\ln \frac{p(z,y|x)\tilde{p}(x)}{q(x|z,y)q(z,y)} dzdx\tag{2}$$
这就是用来做聚类的VAE的loss了。
分步假设 #
啥?就完事了?呃,是的,如果只考虑一般化的框架,$(2)$确实就完事了。
不过落实到实践中,$(2)$可以有很多不同的实践方案,这里介绍比较简单的一种。首先我们要明确,在$(2)$中,我们只知道$\tilde{p}(x)$(通过一批数据给出的经验分布),其他都是没有明确下来的。于是为了求解$(2)$,我们需要设定一些形式。一种选取方案为
$$p(z,y|x)=p(y|z)p(z|x),\quad q(x|z,y)=q(x|z),\quad q(z,y)=q(z|y)q(y)\tag{3}$$
代入$(2)$得到
$$KL\Big(p(x,z,y)\Big\Vert q(x,z,y)\Big) = \sum_y \iint p(y|z)p(z|x)\tilde{p}(x)\ln \frac{p(y|z)p(z|x)\tilde{p}(x)}{q(x|z)q(z|y)q(y)} dzdx\tag{4}$$
其实$(4)$式还是相当直观的,它分布描述了编码和生成过程:
1、从原始数据中采样到$x$,然后通过$p(z|x)$可以得到编码特征$z$,然后通过分类器$p(y|z)$对编码特征进行分类,从而得到类别;
2、从分布$q(y)$中选取一个类别$y$,然后从分布$q(z|y)$中选取一个随机隐变量$z$,然后通过生成器$q(x|z)$解码为原始样本。
具体模型 #
$(4)$式其实已经很具体了,我们只需要沿用以往VAE的做法:$p(z|x)$一般假设为均值为$\mu(x)$方差为$\sigma^2(x)$的正态分布,$q(x|z)$一般假设为均值为$G(z)$方差为常数的正态分布(等价于用MSE作为loss),$q(z|y)$可以假设为均值为$\mu_y$方差为1的正态分布,至于剩下的$q(y),p(y|z)$,$q(y)$可以假设为均匀分布(它就是个常数),也就是希望每个类大致均衡,而$p(y|z)$是对隐变量的分类器,随便用个softmax的网络就可以拟合了。
最后,可以形象地将$(4)$改写为
$$\mathbb{E}_{x\sim\tilde{p}(x)}\Big[-\log q(x|z) + \sum_y p(y|z) \log \frac{p(z|x)}{q(z|y)} + KL\big(p(y|z)\big\Vert q(y)\big)\Big],\quad z\sim p(z|x) \tag{5}$$
其中$z\sim p(z|x)$是重参数操作,而方括号中的三项loss,各有各的含义:
1、$-\log q(x|z)$希望重构误差越小越好,也就是$z$尽量保留完整的信息;
2、$\sum_y p(y|z) \log \frac{p(z|x)}{q(z|y)}$希望$z$能尽量对齐某个类别的“专属”的正态分布,就是这一步起到聚类的作用;
3、$KL\big(p(y|z)\big\Vert q(y)\big)$希望每个类的分布尽量均衡,不会发生两个几乎重合的情况(坍缩为一个类)。当然,有时候可能不需要这个先验要求,那就可以去掉这一项。
实验 #
实验代码自然是Keras完成的了(^_^),在mnist和fashion-mnist上做了实验,表现都还可以。实验环境:Keras 2.2 + tensorflow 1.8 + Python 2.7。
代码实现 #
代码位于:https://github.com/bojone/vae/blob/master/vae_keras_cluster.py
其实注释应该比较清楚了,而且相比普通的VAE改动不大。可能稍微有难度的是$\sum_y p(y|z) \log \frac{p(z|x)}{q(z|y)}$这个怎么实现。首先我们代入
$$\begin{aligned}p(z|x)&=\frac{1}{\prod\limits_{i=1}^d\sqrt{2\pi\sigma_i^2(x)}}\exp\left\{-\frac{1}{2}\left\Vert\frac{z - \mu(x)}{\sigma(x)}\right\Vert^2\right\}\\
q(z|y)&=\frac{1}{(2\pi)^{d/2}}\exp\left\{-\frac{1}{2}\left\Vert z - \mu_y\right\Vert^2\right\}\end{aligned}\tag{6}$$
得到
$$\log \frac{p(z|x)}{q(z|y)}=-\frac{1}{2}\sum_{i=1}^d \log \sigma_i^2(x)-\frac{1}{2}\left\Vert\frac{z - \mu(x)}{\sigma(x)}\right\Vert^2 + \frac{1}{2}\left\Vert z - \mu_y\right\Vert^2 \tag{7}$$
注意其实第二项是多余的,因为重参数操作告诉我们$z = \varepsilon\otimes \sigma(x) + \mu(x),\,\varepsilon\sim \mathcal{N}(0,1)$,所以第二项实际上只是$-\Vert \varepsilon\Vert^2/2$,跟参数无关,所以$$\log \frac{p(z|x)}{q(z|y)}\sim -\frac{1}{2}\sum_{i=1}^d \log \sigma_i^2(x) + \frac{1}{2}\left\Vert z - \mu_y\right\Vert^2 \tag{8}$$
然后因为$y$是离散的,所以事实上$\sum_y p(y|z) \log \frac{p(z|x)}{q(z|y)}$就是一个矩阵乘法(相乘然后对某个公共变量求和,就是矩阵乘法的一般形式),用K.batch_dot实现。
其他的话,读者应该清楚普通的VAE的实现过程,然后才看本文的内容和代码,不然估计是一脸懵的。
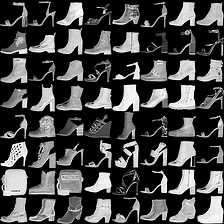
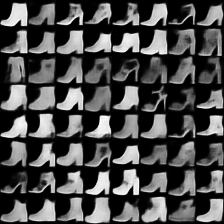
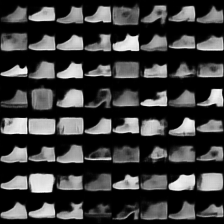
mnist #
这里是mnist的实验结果图示,包括类内样本图示和按类采样图示。最后还简单估算了一下,以每一类对应的数目最多的那个真实标签为类标签的话,最终的test准确率大约有83%,对比这篇文章《Unsupervised Deep Embedding for Clustering Analysis》的结果(最高也是84%左右),感觉应该很不错了。
聚类图示 #
按类采样 #
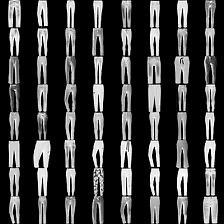
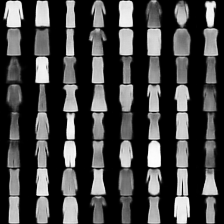
fashion-mnist #
这里是fashion-mnist的实验结果图示,包括类内样本图示和按类采样图示,最终的test准确率大约有58.5%。
聚类图示 #
按类采样 #
总结 #
文章简单地实现了一下基于VAE的聚类算法,算法的特点就是一步到位,结合“编码”、“聚类”和“生成”三个任务同时完成,思想是对VAE的loss的一般化。
感觉还有一定的提升空间,比如式$(4)$只是式$(2)$的一个例子,还可以考虑更加一般的情况。代码中的encoder和decoder也都没有经过仔细调优,仅仅是验证想法所用。
转载到请包括本文地址:https://kexue.fm/archives/5887
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Sep. 17, 2018). 《变分自编码器(四):一步到位的聚类方案 》[Blog post]. Retrieved from https://kexue.fm/archives/5887
@online{kexuefm-5887,
title={变分自编码器(四):一步到位的聚类方案},
author={苏剑林},
year={2018},
month={Sep},
url={\url{https://kexue.fm/archives/5887}},
}








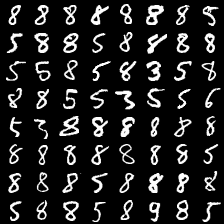
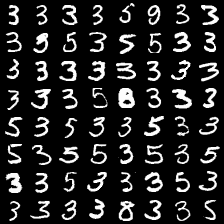
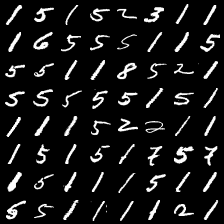
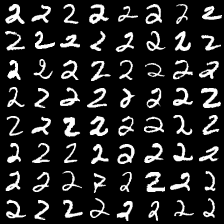
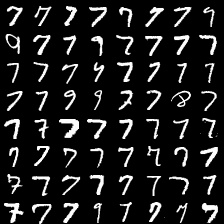
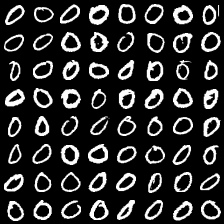
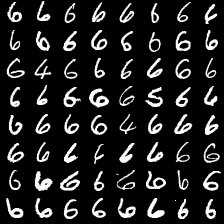

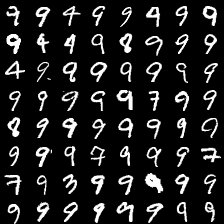




























September 18th, 2018
你好,看了你的文章,对于vae的理解又多了一些。非常感谢。
在这里,我想问几个关于vae训练的问题。希望您能帮忙解答。
1. vae的encoder和decoder在设计时有什么注意事项呢。比如我想要预训练好的resnet50作为vae的encoder,然后用随机初始化的resnet18(结构类似,中间用反卷积)作为解码器。请问这个结构设计是否合理呢。
2. vae在训练的时候,有没有一些技巧呢。经常容易出现kl loss下降到某个点,然后就一直上升。但是mse loss一直下降。请问这个现象为什么会出现呢。
3. vae中mse loss和kl loss之间是否需要有weights呢?一般对于mnist数据,mse loss比较小,但是当使用224x224x3大小的图片来训练的话,mse loss就会非常大,远远超过kl loss。
问的比较乱,希望能回答一下。非常感谢。
真心请教,希望博主能够帮忙解答一下。
不好意思,信息太多,一下子忘记了。
1、decoder和encoder在结构上一般互逆,一般都是自己写的结构,网上也有很多现成的例子,找来看看对比一下规律就明白了。我还没见过直接用预训练的模型的。毕竟像resnet50这样的模型太庞大了,还要引入一个同样庞大的decoder,不大现实;
2、我也没有特别研究技巧,但是VAE的生成质量一般直接看总的loss,不需要分别观察两部分loss;
3、mse和kl loss之间可以考虑加入一个权重。但是要注意“mse loss很大远超过kl loss”表明你的模型设计上就不合理,因为虽然VAE允许降维,但是输入x和隐变量z的维度至少要在同一数量级才能保证比较好的生成效果。在这个前提下,事实上两者在量级上不会差别很大。
非常感谢
September 20th, 2018
(4) 到(5)的改写能详细点么?自己推了一下,总是和(5)式不一致,不知道问题在哪里。。。
$$\begin{aligned}&\sum_y \iint p(y|z)p(z|x)\tilde{p}(x)\ln \frac{p(y|z)p(z|x)\tilde{p}(x)}{q(x|z)q(z|y)q(y)} dzdx\\
=&\mathbb{E}_{x\sim\tilde{p}(x)}\left[\sum_y \int p(y|z)p(z|x)\ln \frac{p(y|z)p(z|x)\tilde{p}(x)}{q(x|z)q(z|y)q(y)} dz\right]\\
=&\mathbb{E}_{x\sim\tilde{p}(x)}\left[\sum_y \int p(y|z)p(z|x)\left(-\ln q(x|z) + \ln\frac{p(z|x)}{q(z|y)}+\ln\frac{p(y|z)}{q(y)}+\ln \tilde{p}(x) \right)dz\right]
\end{aligned}$$
$\ln \tilde{p}(x)$相当于常数,不影响结果,可以去掉,所以结果等价于
$$\begin{aligned}&\mathbb{E}_{x\sim\tilde{p}(x)}\left[\sum_y \int p(y|z)p(z|x)\left(-\ln q(x|z) + \ln\frac{p(z|x)}{q(z|y)}+\ln\frac{p(y|z)}{q(y)}\right)dz\right]
\end{aligned}$$
重参数运算实际上就相当于完成了$p(z|x)dz$这部分积分,所以等价于
$$\begin{aligned}&\mathbb{E}_{x\sim\tilde{p}(x)}\left[\sum_y p(y|z)\left(-\ln q(x|z) + \ln\frac{p(z|x)}{q(z|y)}+\ln\frac{p(y|z)}{q(y)}\right)\right],z\sim p(z|x)
\end{aligned}$$
剩下的在文中已经做了推导。
请问第二项的p(y|z)怎么提到dz积分外面来了呢?难道p(y|z)跟z无关?谢谢
感谢提出这个问题,经检查确实是一个bug,已经修正,对结果有些不小不大的影响。
赞速度~
老师,请问,修改完bug,最终的结果应该是什么?
就是本文。
大神,$\mathbb{E}_{x\sim\tilde{p}(x)}\left[\sum_y p(y|z)\left(-\ln q(x|z) + \ln\frac{p(z|x)}{q(z|y)}+\ln\frac{p(y|z)}{q(y)}\right)\right],z\sim p(z|x)
$变换以后应该是$\mathbb{E}_{x\sim\tilde{p}(x)}\Big[- \sum_y p(y|z)\log q(x|z) + \sum_y p(y|z) \log \frac{p(z|x)}{q(z|y)} + KL\big(p(y|z)\big\Vert q(y)\big)\Big],\quad z\sim p(z|x) $,
你的公式5中第一项没有$\sum_y p(y|z)$,只有$\log q(x|z)$,把$\sum_y p(y|z)$去掉了,不理解。
@niu|comment-16034
如果连$\sum_y p(y|z)=1$都不理解,那你是怎么看到第四篇的?
可是我看到你后两项都保留p(y|z),既然p(y|z)的和为1,那为什么后两项不去掉?
@niu|comment-16056
建议你去补习一下基本的数学运算常识。第一项是$\sum_y p(y|z)$,后两项哪里是$\sum_y p(y|z)$了?
请问一下,在公式 $(4)$ 和公式 $(5)$ 之间是不是还缺少一个求期望的过程?如下公式$(**)$所示。
\begin{align}&\mathbb{E}_{x\sim\tilde{p}(x)}\left[\sum_y \int p(y|z)p(z|x)\left(-\ln q(x|z) + \ln\frac{p(z|x)}{q(z|y)}+\ln\frac{p(y|z)}{q(y)}\right)dz\right] \tag{4}
\end{align}
\begin{align}&\mathbb{E}_{x\sim\tilde{p}(x)}\left[\sum_y \mathbb{E}_{z\sim{p}(z|x)}\left[ p(y|z)p(z|x)\left(-\ln q(x|z) + \ln\frac{p(z|x)}{q(z|y)}+\ln\frac{p(y|z)}{q(y)}\right)\right]\right],z\sim p(z|x)\tag{**}
\end{align}
\begin{align}
&\mathbb{E}_{x\sim\tilde{p}(x)}\left[\sum_y p(y|z)\left(-\ln q(x|z) + \ln\frac{p(z|x)}{q(z|y)}+\ln\frac{p(y|z)}{q(y)}\right)\right],z\sim p(z|x) \tag{5}
\end{align}
@ak422|comment-18541
不明白你要表达什么。
你的$(**)$应该是
$$\mathbb{E}_{x\sim\tilde{p}(x)}\left[\sum_y \mathbb{E}_{z\sim{p}(z|x)}\left[ p(y|z)\left(-\ln q(x|z) + \ln\frac{p(z|x)}{q(z|y)}+\ln\frac{p(y|z)}{q(y)}\right)\right]\right],z\sim p(z|x)$$
修正了,然后呢?照样是得到$(5)$呀。你是说我跳步太多了?
重参数运算实际上就相当于完成了p(z|x)dz这部分积分 这个怎么理解呀 老师
因为对p(z|x)的积分,就是相当于在p(z|x)中采样呀。
苏老师,我还是不太理解,为什么相当于p(z|x)中采样,那个积分好就可以拿掉?
积分就相当于求期望,重参数就相当于采样一个点来估计期望,同时保留了梯度。
哦,苏老师,是不是蒙特卡洛估计?
苏神好呀,请问将$ln\frac{p(y|z)p(z|x)\widetilde{p}(x)}{q(x|z)q(z|y)q(y)}$这一项拆分为$-lnq(x|z)$, $ln\frac{p(z|x)}{q(z|y)}$, $ln\frac{p(y|z)}{q(y)}$,$ln\widetilde{p}(x)$这四项背后的指导思想是什么呢? 经过前面的阅读,我模糊地认为 $-lnq(x|z)$这一项被拆出是对应着重构损失, $ln\frac{p(y|z)}{q(y)}$这一项被拆出是为了结合括号为的$p(y|z)$组成KL散度, $ln\widetilde{p}(x)$这一项是一个可忽略的常数项。 所以剩余的$ln\frac{p(z|x)}{q(z|y)}$这一部分仅仅是因为它被剩下了么?还是说它也对应着什么目前我还不知道的含义?
因为分布的随机变量相同
哦哦,原来是这样,恍然大悟
October 23rd, 2018
请问博主,这种聚类的方法,能用在分类的问题上?
October 24th, 2018
我的数据是带正负样本的,苏老师能帮忙解释一下吗,感谢~~。
October 24th, 2018
问题是:我的数据是带正负样本的数据,希望训练模型,将未知的样本分类,还希苏老师能帮忙解疑
直接训练一个二分类模型不就行了?为什么要涉及到聚类?
November 20th, 2018
苏神,我想问代码中cat_loss = K.mean(y * K.log(y + K.epsilon()), 0)具体是怎么由第三项loss推导出来的啊?
其中K.epsilon()怎么理解啊?跟之前的重参数技巧中的 epsilon是一个东西么?
K.epsilon()是一个很小的正数,防止log(0)的出现......
q(z|y)的均值μy是由一层网络得到的吧?
是
苏神,还是不懂cat_loss = K.mean(y * K.log(y + K.epsilon()), 0)具体是怎么由第三项loss推导出来的,能具体解释一下吗
$$\begin{aligned}K(p(y|x)\Vert q(y))=&\sum_y p(y|x)\log \frac{p(y|x)}{q(y)}\\=&\sum_y p(y|x)\log p(y|x) - \sum_y p(y|x)\log q(y)\end{aligned}$$
注意类别的先验分布被假设为均匀分布,也就是$q(y)$是个常数。所以$\sum_y p(y|x)\log q(y)=\log q(y)$只是一个常数,因此只剩下$\sum_y p(y|x)\log p(y|x)$这一项。
December 6th, 2018
大佬,小萌新有点看不懂代码中的Gaussian类,是怎么求出μy的呀?这个的输入是z么?是的话,但要求的不是从y到z的均值么,输入应该是y吧?z * 0 + K.expand_dims(self.mean, 0)这个返回值怎么理解,为啥要乘0啊?希望大神能帮忙解答,打扰了
self.mean的shape是(num_classes, latent_dim),K.expand_dims之后就是(1, num_classes, latent_dim)。
z = K.expand_dims(z, 1)之后,z的shape就是(batch_size, 1, latent_dim)。
z * 0 + self.mean的shape是(batch_size, num_classes, latent_dim),但是跟z无关,说白了就是把self.mean重复batch_size次...
苏老师,我看您在github上的代码和您这里写的不一样。Github中,
def call(self, inputs):
z = inputs # z.shape=(batch_size, latent_dim)
z = K.expand_dims(z, 1)
return z - K.expand_dims(self.mean, 0)
我加人了几句代码,输出z, test1=K.expand_dims(self.mean, 0); test2=z - K.expand_dims(self.mean, 0)的shape,输出结果如下:
(None, 1, 20)
(1, 10, 20)
(None, 10, 20)
Epoch 1/50
(100, 1, 20)
(1, 10, 20)
(100, 10, 20)
我不知道z 和 K.expand_dims(self.mean, 0)的shpae不同,为什么还能相减?
另外,关于这个函数还有2个问题向您请教。
1. 下面这句话,是输入为class的个数(10),输出为z的均值(每个都是latent_dim长度的向量?
self.mean = self.add_weight(name='mean',
shape=(self.num_classes, latent_dim),
initializer='zeros')
2. 我看有的资料上写,自定义层的build函数最好,要有这么一句话,请问您是不是必须?
super(MyLayer, self).build(input_shape) # 一定要在最后调用它
对于第一个问题:请学好numpy、tf或pytorch等数组处理工具的常规用法;
对于第二个问题:请理解本文公式的各项含义;
对于第三个问题:请学好Python的面向对象编程。
December 7th, 2018
哦,这个理解了,感谢!
但z_prior_mean = gaussian(z)中的调用输入为z,是对的么?不应该是求出的y么?还是我根本就没理解.....
z_prior_mean仅仅是正态分布$q(x|y)$的参数(均值)。
输入采样来的z,通过全连接层得到均值,对么?
不是,z_prior_mean仅仅是正态分布$q(x|y)$的参数(均值),z_prior_mean仅仅是正态分布$q(x|y)$的参数(均值),z_prior_mean仅仅是正态分布$q(x|y)$的参数(均值)。
$q(x|y)$是$y$的条件概率,哪里会跟$z$有关?
苏神,可以具体讲一下gaussian(z)函数参数的训练过程吗?这个函数觉得不太好理解
这个真不好说...注释我也注释了,我只能说“你可以尝试想想自己来写会怎么写”,然后对比我的代码,估计就能懂了~
苏老师,您定义的这个Gaussian我也感觉很难理解,您能否给出一点解释。我看了自定义Layer的资料,我目前看到的,自定义Layer中的weight是和输入进行作用,得到输出。而您这里的weight看不出与输入的作用,感觉这些weight就直接对应公式8最后一项的uy了。请您指点,谢谢
苏老师,请问您这里的q(x|y)是否应该是q(z|y),对应于公式(8)?我没有在正文中找到q(x|y)
苏老师,我上面没有说明白问题,我主要的困惑是Gaussian这个层中的self.mean以layer的weight形式定义,但是如何在反向传播中体现,我想不出来gaussian(z)的网络结构图。我现在觉得这个self.mean就像网络结构图中的bias,从z中被减去,得到z_prior_mean。请您指点。
我不知道你们究竟在困惑什么。Keras模型里边所有操作都需要封装成一个层,所以我才定义了这么一个层,它实际上就是z减去一个可训练向量,对应于公式$(8)$里边的$z-\mu_y$这一步。我根本不理解为什么会卡这个操作上,难道只因为我我起了一个叫做Gaussian的名字么?还是说源于对Keras的不理解?如果是后者,不是应该去补习一下Keras么?
噢噢,当时可能糊涂了,上面讨论中所有的$q(x|y)$实际上都是指$q(z|y)$。
December 17th, 2018
苏神,K.batch_dot(K.expand_dims(y, 1), kl_loss)中axes值是多少啊?我自己推了一遍,感觉有点不对...
默认是[-1, -2]
January 11th, 2019
苏神,程序好像跑不对呀,y_train_pred的55000个值是一样的。
反正我跑对了~(Python2.7 + Keras 2.2.4 + tf 1.8)
苏神,我python是3.6,这个应该没有影响吧,然后训练的时候在跑完第一个epoch就下降到了7点多,然后后面一直没有下降,这种情况不正常额
仅供参考:
1、我跑成功了;2、我没有造假;3、你的环境跟我的环境不一致。
我不知道python3会不会有影响,但作为基本的尊重,我认为你至少要在“完全复现环境的前提下还跑失败”再来提问,因为我不是python升级的debuger。
你好,我用tensorflow复现的时候也遇到了同样的问题,请问您找到bug了吗
谨慎起见,我刚才把github上的代码原封不动地重跑了一次。结果如下:
第1个epoch:(loss: 57.3568 - val_loss: 43.7675)
第50个epoch:(loss: 36.6223 - val_loss: 36.5311)
train acc: 0.873616666667,test acc: 0.8769
所以,开源代码的实现是完全没有问题的~如果你用其他语言复现不了,那么只能说明是实现上的错误,不是本模型的bug;如果你直接跑我开源的代码还是复现不了,请检查环境是否完全一致,如不一致,请自行更正。
苏神您好,我运行了您的代码确实和您的结果一样。出现问题是因为我把输入换成了2维数据并且将卷积层改成了全连接,经过多次试验发现,需要仔细调整3个loss的权重才能达到良好的聚类效果。我自己猜测是由于数据维度明显降低导致前两个loss的值显著缩小。不知道苏神您怎么看?
您好,我也在做二维数据,请问下方便分享下调参经验吗